4.1. Система Коши-Римана

Система линейных однородных дифференциальных уравнений первого порядка в частных производных с двумя независимыми переменными x и y

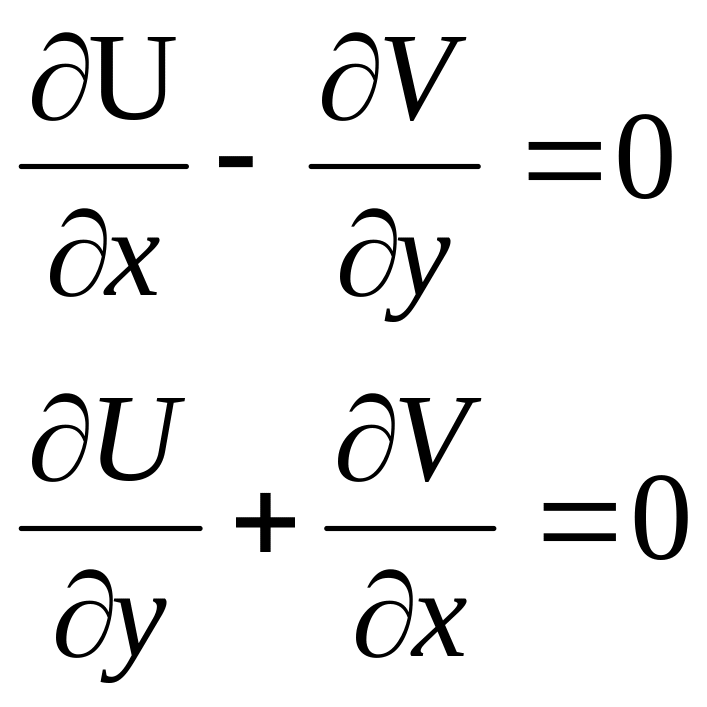(4.1.1)

называется системой Коши-Римана. Это система эллиптического типа.

Напомним, что система дифференциальных уравнений, матричная запись которой имеет вид

где

U=

относится к эллиптическому типу, если квадратичная форма

положительно (или отрицательно) определена.

Поскольку в случае системы (4.1.1) имеем:

и квадратичная форма

оказывается положительно определенной, система Коши-Римана является системой эллиптического типа.

Если - произвольная гармоническая функция, т.е. если она удовлетворяет уравнению Лапласа

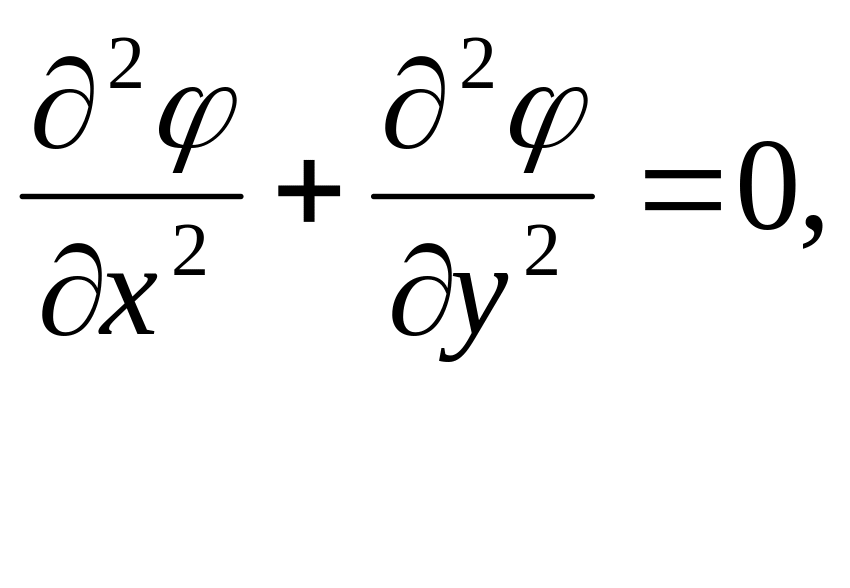
то пара функций является решением системы Коши-Римана, что несложно проверить непосредственной подстановкой:

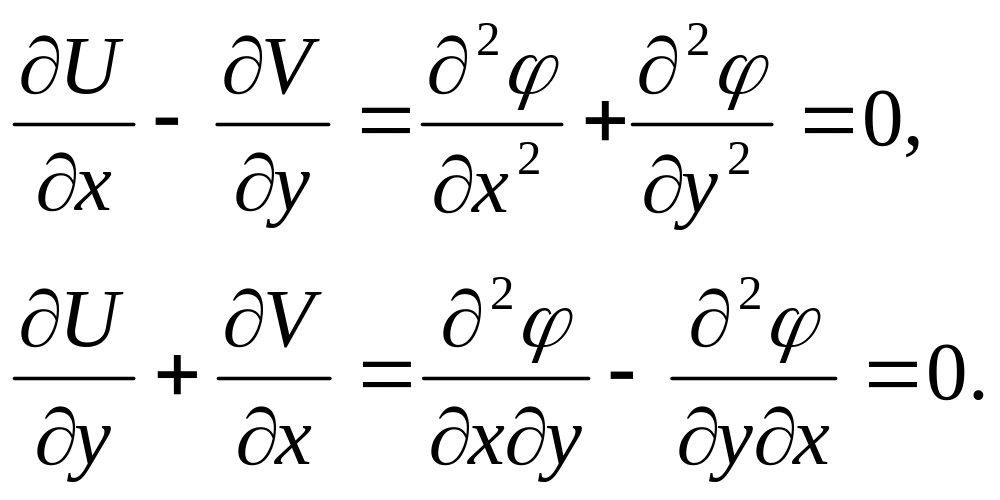
Последнее равенство имеет место в силу известной из математического анализа теоремы о непрерывных смешанных производных. Ниже будет показано, что действительная и мнимая части и функции , аналитической в некоторой области, обладают дифференцируемыми (следовательно, и непрерывными) частными производными любого порядка. Из непрерывности функций и следует непрерывность функций и , а непрерывные смешанные производные и всегда равны.

4.2. Дифференцируемость и аналитичность

Функция , где и – действительные функции действительных переменных , а -мнимая единица, называется непрерывной, если непрерывны функции и .

Легко проверить, что это определение равносильно следующему:

Функция , определенная в области D, непрерывна в точке , если для любого существует такое , что для всех из круга выполняется неравенство

Так же, как и в анализе функций действительного переменного, можно дать и другие определения непрерывности функции конечной точке .

Функция , непрерывная в каждой точке области , называется непрерывной в этой области что, как правило, обозначается следующим образом .

Среди теорем о функциях, непрерывных в области, отметим (без доказательств) две:

1. Функция , непрерывная в замкнутой области , ограничена в этой области, то есть существует такая постоянная , что для всех из

2. Функция , непрерывная в замкнутой области , принимает в ней свое максимальное и свое минимальное (по модулю) значения.

Эти теоремы остаются в силе также для функций, непрерывных на замкнутых кривых, или на отрезках линий, содержащих свои концы. Из класса непрерывных функций можно выделить подкласс функций, которые допускают дифференцирование. Определение дифференцируемости функции комплексного переменного можно дать совершенно аналогично определению дифференцируемости функции действительного переменного:

Функция , определенная в области , называется дифференцируемой в точке , если существует конечный предел

,

не зависящий от способа стремления величины к нулю. Этот предел называется производной функции в точке и обозначается символом

Очевидно, что для дифференцируемости функции необходимо, чтобы были дифференцируемы функции и . Однако дифференцируемости функций и отнюдь не достаточно для дифференцируемости функции , как показывает пример . Действительно, функции и дифференцируемы, причем

С другой стороны, для любых действительных и, следовательно,

,

а для любых чисто мнимых , так что

,

то есть производная функции не существует.

Таким образом, для дифференцируемости функции функции и должны быть не только дифференцируемы, но еще и связаны некоторыми соотношениями.

Теорема 1. Для того чтобы функция , определенная в некоторой области , была дифференцируема в точке этой области как функция комплексного переменного, необходимо и достаточно, чтобы функции и были дифференцируемы в той же точке (как действительные функции двух действительных переменных) и чтобы, кроме того, выполнялись условия Коши-Римана.

(4.2.1)

В некоторых руководствах по теории аналитических функций условия (4.2.1) называют условиями Даламбера-Эйлера.

При выполнении всех условий теоремы 1 производная (или ) может быть представлена в одной из следующих форм:

Пользуясь символами комплексного дифференцирования

и замечая, что

(4.2.2)

условиям Коши-Римана (4.2.1) можно придать вид

. (4.2.3)

Функция , дифференцируемая в каждой точке некоторой области , называется аналитической (иначе регулярной, моногенной или голоморфной) в этой области. Заметим, что такое определение аналитической функции предполагает ее однозначность в области , ибо понятия предела и производной определены исключительно для однозначных функций.

Можно обобщить понятие аналитичности, распространив его и на многозначные функции.

Замечание 1. Из теоремы 1 следует, что функция , дифференцируемая в области относительно и , будет аналитической в этой области тогда и только тогда, когда во всех точках области выполняется условие (4.2.3)

,

при этом

. (4.2.5)

Замечание 2. Если и функции непрерывны и обладают в некоторой области непрерывными частными производными первого порядка, а функция аналитична в этой области, то в силу (4.2.4)

(4.2.6)

Замечание 3. Во многих случаях важно иметь условия дифференцируемости функции комплексного переменного в точке , выраженные с помощью полярных координат . Эти условия (необходимые и достаточные) таковы:

1) Функции и являются дифференцируемыми функциями и ;

2) Их частные производные связаны соотношениями Коши-Римана

(4.2.7)

Легко можно получить формулы для вычисления в полярных координатах:

(4.2.8)

и

. (4.2.9)

Замечание 4. Понятие функции, аналитической в некоторой области , характеризуется целым рядом замечательных и притом довольно разнообразных свойств, которые логически между собой эквивалентны. Поэтому каждое из свойств может быть положено в основу определения понятия аналитической функции в некоторой области -плоскости. Приведем их:

Свойство 1. Функция имеет производную в каждой точке области .

Свойство 2. В области действительная и мнимая части и функции являются сопряженными гармоническими функциями.

Свойство 3. Каждая функция , однозначная и непрерывная в некоторой односвязной области и такая, что интеграл от , взятый по любому треугольному контуру, принадлежащему области , равен нулю.

Свойство 4. В любом концентрическом круге меньшего радиуса функция может быть равномерно приближена многочленами.