Рекомендации к решению и оформлению задач по данной теме

Задачи на формулу полной вероятности чаще всего используется, когда эксперимент можно разделить на два этапа, и на первом этапе можно выделить полную систему попарно несовместных событий . Тогда вероятность любого события А, связанного со всем экспериментом вычисляется по формуле .

Задачи на испытания Бернулли обычно имеют физическую или техническую постановку. Самое главное при решении таких задач – найти испытания Бернулли, что часто нелегко сделать. Придерживайтесь следующей последовательности решения:

а) определите, что является отдельным испытанием Бернулли;

б) назначьте “успех” и “неудачу”;

в) подсчитайте общее количество испытаний ;

г) вычислите вероятность успеха ;

д) свяжите искомые вероятности с вероятностью иметь успехов в испытаниях, найдите значение ;

е) воспользуйтесь формулой Бернулли или, если это допустимо, формулой Пуассона.

Формула Байеса имеет большое практическое применение. Она позволяет уточнить значение вероятности события (гипотезы) после завершения эксперимента, когда событие А уже произошло.

Пример оформления задачи.

Имеются 3 одинаковые урны. В первой урне два белых и один черный шар; во второй – три белых и один черный; в третьей – два белых и два черных шара. Наугад из одной из урн вынимается один шар. Найти вероятность того, что этот шар белый.

Решение. Задачу можно разделить на два этапа. На первом этапе выбираем урну. На втором этапе – вынимается шар из уже выбранной урны.

Обозначим события:

– выбор первой урны;

– выбор второй урны;

– выбор третьей урны;

– появление белого шара.

Тогда – вероятность выбора первой, второй и третьей урны соответственно; – вероятность появления белого шара.

Т.к. задачу можно разделить на два этапа, справедлива формула полной вероятности:

Найдем отдельно каждую вероятность в этой формуле. Т.к. по условию все уровни одинаковые, то выбор каждой урны – равновероятен, т.е. . По формуле классической вероятности, выбор первой урны равен (полное количество исходов – выбор какой-нибудь урны ; количество исходов, заканчивающихся выбором именно первой урны ):

.

Условные вероятности выбора белого шара при условии, что он выбирается из первой, второй и третьей урны соответственно ( ) также найдем по формуле классической вероятности.

Выбор белого шара из первой урны соответственно равен (количество способов вынимания из первой урны какого-нибудь шара равен количеству шаров в этой урне , количество исходов, благоприятствующих появлению белого шара равно количеству белых шаров в урне, т.е. ):

.

Аналогичные рассуждения для других урн дают следующие результаты:

Подставляя полученные значения в формулу полной вероятности, получаем:

Ответ:

Имеются 3 одинаковые урны. В первой урне два белых и один черный шар; во второй – три белых и один черный; в третьей – два белых и два черных шара. Наугад из одной из урн вынимается один шар. Этот шар оказывается белым. Найти вероятность того, что этот шар был вынут из первой урны.

Решение. В данной задаче исход эксперимента известен – вынут белый шар. Необходимо найти вероятность гипотезы, т.е. найти урну, из которой он вынут.

Обозначим исход эксперимента:

– появление белого шара

и гипотезы

– выбор шара из первой урны;

– выбор шара из второй урны;

– выбор шара из третьей урны;

Тогда – вероятность выбора первой, второй и третьей урны соответственно; – вероятность появления белого шара; условные вероятности выбора белого шара при условии, что он выбирается из первой, второй и третьей урны соответственно ; – условная вероятность выбора белого шара из первой урны (ее необходимо найти).

Т.к. исход эксперимента известен, необходимо уточнить вероятность гипотезы, то справедлива формула Байеса :

.

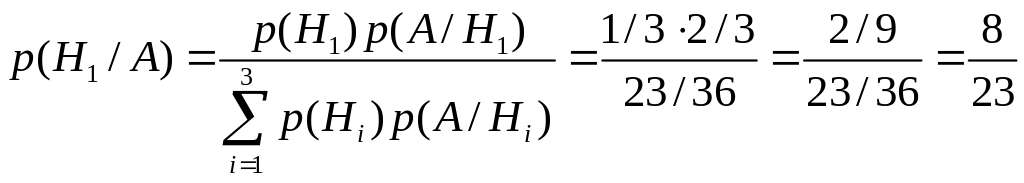Здесь были использованы численные значения, полученные в предыдущем примере.

Производится 4 выстрела. Вероятность попадания при одном выстреле равна 0,2. Найти вероятность попадания а) точно 3 раз; б) хотя бы одного попадания.

Решение. Данная задача рассматривает испытания Бернулли, т.к. выполнены все условия, каким должны удовлетворять эти испытания. Под испытанием здесь понимается – выстрел.

а) выстрелы являются независимыми испытаниями;

б) каждый выстрел (испытание) может закончится двумя исходами : «успех» – попадание; «неудача» – промах.

в) вероятность «успеха» в каждом испытании одинакова и равна .

В этом случае справедлива формула Бернулли.

а) Вероятность успехов при испытаниях равна:

.

Здесь . .

Подставляем эти значения:

.

б) вероятность хотя бы одного попадания, т.е. хотя бы одного успеха ( ) легче найти, используя противоположное событие, смысл которого состоит в попадание раз, т.е. раз:

.

Здесь . (здесь учтено, что ).

.

Ответ: а) ; б) .