
- •080100.62 «Экономика»
- •Пояснительная записка
- •Методические рекомендации по выполнению заданий контрольной работы
- •Тема 1.
- •Алгебра событий
- •Классическое определение вероятности
- •Относительная частота. Статистическое определение вероятности
- •Основные формулы комбинаторики
- •Рекомендации к решению и оформлению задач по данной теме
- •Тема 2.
- •Теорема сложения вероятностей
- •Теорема умножения вероятностей
- •Вероятность появления хотя бы одного события
- •Геометрическая вероятность
- •Рекомендации к решению и оформлению задач по данной теме
- •Тема 3.
- •Формула полной вероятности
- •Формула Байеса (теорема гипотез)
- •Приближение Пуассона для схемы Бернулли
- •Рекомендации к решению и оформлению задач по данной теме
- •Тема 4.
- •Дискретные случайные величины
- •Распределения дискретной случайной величины
- •Тема 5.
- •Экспоненциальное распределение
- •Тема 6.
- •Математическое ожидание.
- •1. Биномиальное распределение.
- •2. Закон Пуассона.
- •3. Равномерное распределение.
- •4. Нормальное распределение.
- •Тема 7.
- •Задания контрольной работы по дисциплине «Теория вероятностей и математическая статистика» Вариант № 1
- •Вариант № 2
- •Вариант № 3
- •Вариант № 4
- •Вариант № 5
- •Вариант № 6
- •Вариант № 7
- •Вариант № 8
- •Вариант № 9
- •Вариант № 10
- •Литература
Распределения дискретной случайной величины
Для дискретной случайной величины наибольшее применение нашли четыре распределения: равномерное, биномиальное, Пуассона и геометрическое (не путать с геометрической вероятностью!!!).
Равномерное распределение.
Примером вероятностной модели, в которой
появляется равномерно распределенная
случайная величина, является случайный
выбор шара из урны, в которой находятся
одинаковые шары с номерами
![]() .
В этом случае
- номер выбранного шара.
.
В этом случае
- номер выбранного шара.
Равномерное распределение имеет вид:
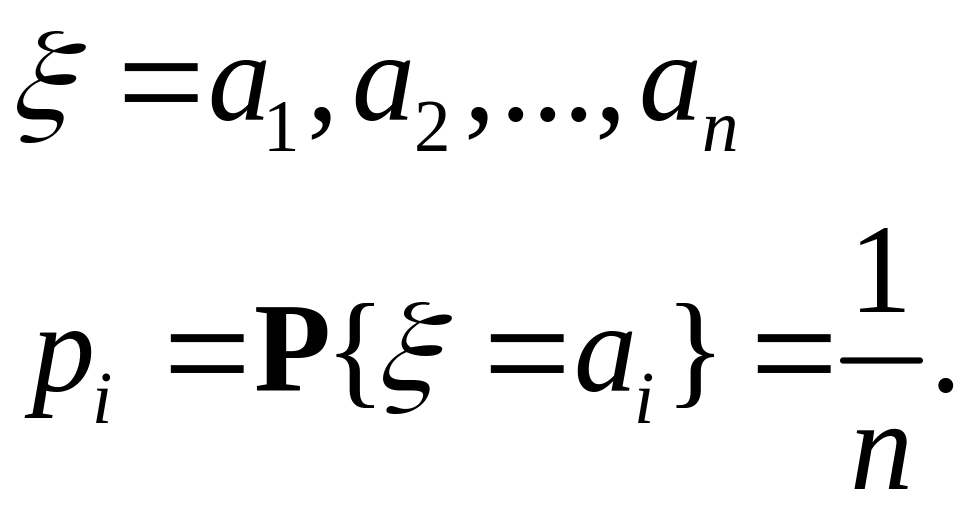
Биномиальное распределение.
Примером вероятностной модели, в которой появляется биномиальное распределение, является последовательность испытаний Бернулли с вероятностью успеха в одном испытании . В этом случае - число успехов в испытаниях.
Биномиальное распределение имеет вид:
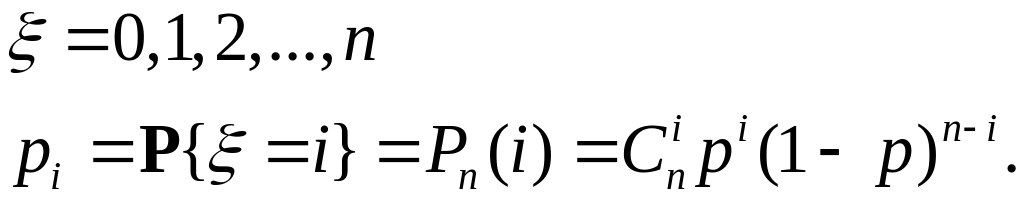
( – вероятность успеха в каждом испытании).
Пример. Составим ряд распределения
случайной величины
![]() – числа попаданий при 5 выстрелах, если
вероятность попадания при одном выстреле
равна 0,8.
– числа попаданий при 5 выстрелах, если
вероятность попадания при одном выстреле
равна 0,8.
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом, ряд распределения имеет вид:
|
0 |
1 |
2 |
3 |
4 |
5 |
|
0.00032 |
0.0064 |
0.0512 |
0.2048 |
0.4096 |
0.32728 |
Распределение Пуассона.
Пуассоновское распределение наиболее часто появляется в двух моделях:
а) пуассоновский поток событий - в этом
случае - число
событий, происходящих за время
![]() (пуассоновский поток событий - это поток
событий, обладающий тремя хорошими
свойствами: стационарностью, марковостью,
ординарностью.);
(пуассоновский поток событий - это поток
событий, обладающий тремя хорошими
свойствами: стационарностью, марковостью,
ординарностью.);
б) испытания Бернулли - в этом случае - число успехов в испытаниях.
Помните, что в испытаниях Бернулли
пуассоновское распределение является
приближенным. Оно применимо, если число
испытаний n очень велико, а вероятность
успеха
очень мала (точнее:
![]() ).
).
Пуассоновское распределение имеет вид:
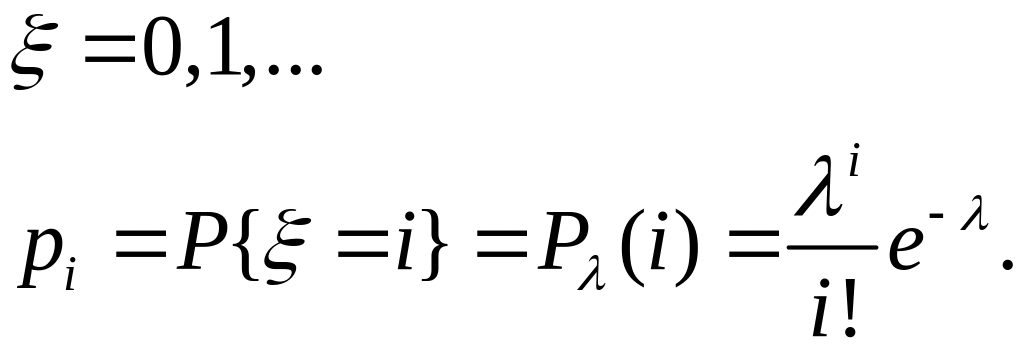
Смысл параметра :
а) в случае пуассоновского потока событий
![]() ,
где
,
где
![]() - интенсивность потока (среднее число
событий в единицу времени);
- интенсивность потока (среднее число
событий в единицу времени);
б) в случае испытаний Бернулли
![]() .
.
Геометрическое распределение.
Примером вероятностной модели для геометрического распределения также могут служить испытания Бернулли. Здесь случайная величина - число успехов до первой неудачи.
Геометрическое распределение имеет вид:

где p- вероятность успеха в одном испытании.
Тема 5.
Функция распределения и плотность распределения непрерывной случайной величины, их взаимосвязь и свойства. Равномерное, нормальное, показательное распределения для непрерывных случайных величин.
Определение и свойства функции
распределения сохраняются и для
непрерывной случайной величины, для
которой функцию распределения можно
считать одним из видов задания закона
распределения. Но для непрерывной
случайной величины вероятность каждого
отдельного ее значения равна 0. Это
следует из свойства 4 функции распределения:
![]() Поэтому для такой случайной величины
имеет смысл говорить только о вероятности
ее попадания в некоторый интервал.
Поэтому для такой случайной величины
имеет смысл говорить только о вероятности
ее попадания в некоторый интервал.
Вторым способом задания закона распределения непрерывной случайной величины является так называемая плотность распределения (плотность вероятности, дифференциальная функция).
Определение 5.1. Функция f(x), называемая плотностью распределения непрерывной случайной величины, определяется по формуле:
![]() ,
,
то есть является производной функции распределения.
Свойства плотности распределения.
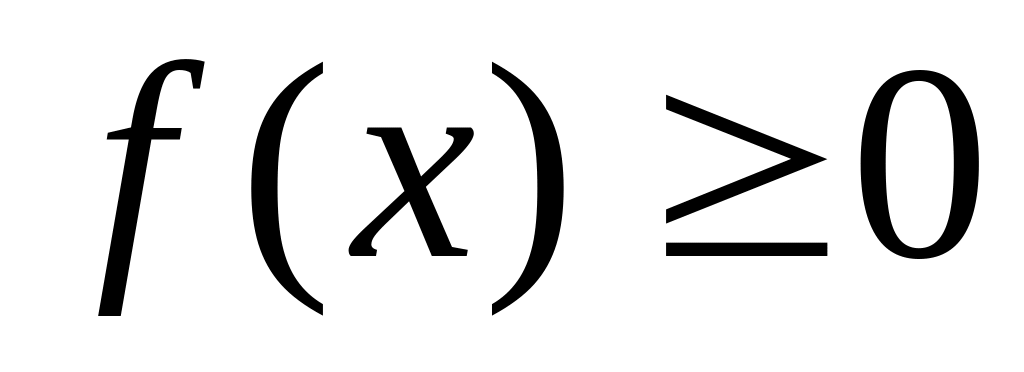 ,
так как функция распределения является
неубывающей.
,
так как функция распределения является
неубывающей.
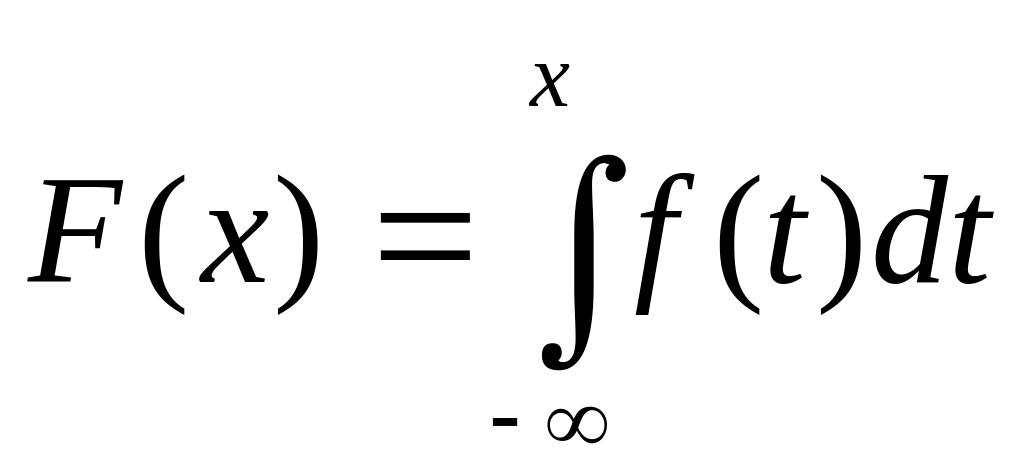 ,
что следует из определения плотности
распределения.
,
что следует из определения плотности
распределения.
Вероятность попадания случайной величины в интервал
 определяется формулой
определяется формулой
![]()
Действительно,
![]()
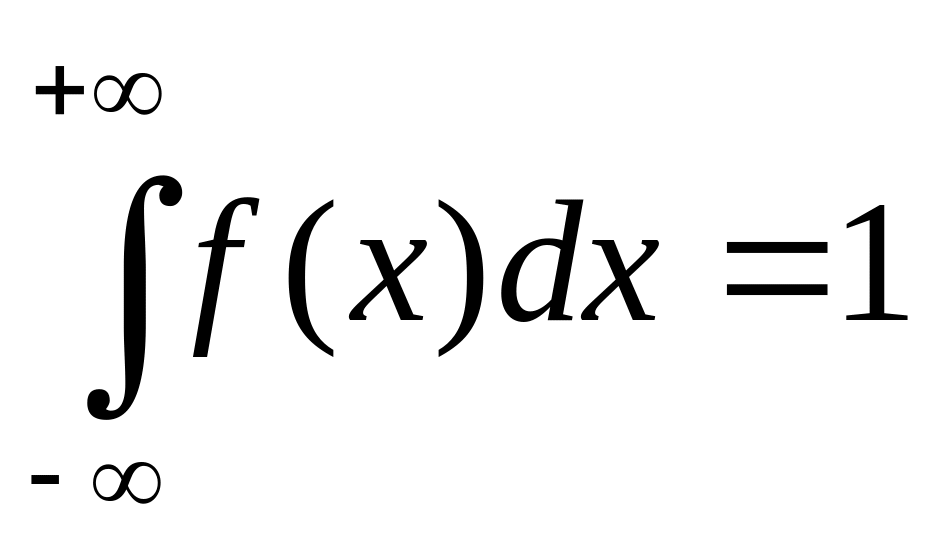 (условие нормировки).
(условие нормировки).
Его справедливость следует из того, что
![]() а
а
![]()
 так как
так как
 при
при

Таким образом, график плотности
распределения представляет собой
кривую, расположенную выше оси Ох,
причем эта ось является ее горизонтальной
асимптотой при
![]() (последнее справедливо только для
случайных величин, множеством возможных
значений которых является все множество
действительных чисел). Площадь
криволинейной трапеции, ограниченной
графиком этой функции, равна единице.
(последнее справедливо только для
случайных величин, множеством возможных
значений которых является все множество
действительных чисел). Площадь
криволинейной трапеции, ограниченной
графиком этой функции, равна единице.
Замечание. Если все возможные
значения непрерывной случайной величины
сосредоточены на интервале
,
то все интегралы вычисляются в этих
пределах, а вне интервала
![]() .
.
Пример 1. Плотность распределения непрерывной случайной величины задана формулой
![]()
Найти: а) значение константы
;
б) вид функции распределения; в)
![]() .
.
Решение. а) значение константы найдем из свойства 4:
![]() откуда
откуда
![]() .
.
б)
![]()
в)
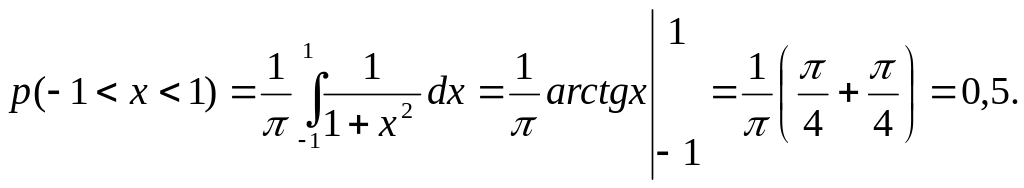
Пример 2. Функция распределения непрерывной случайной величины имеет вид:
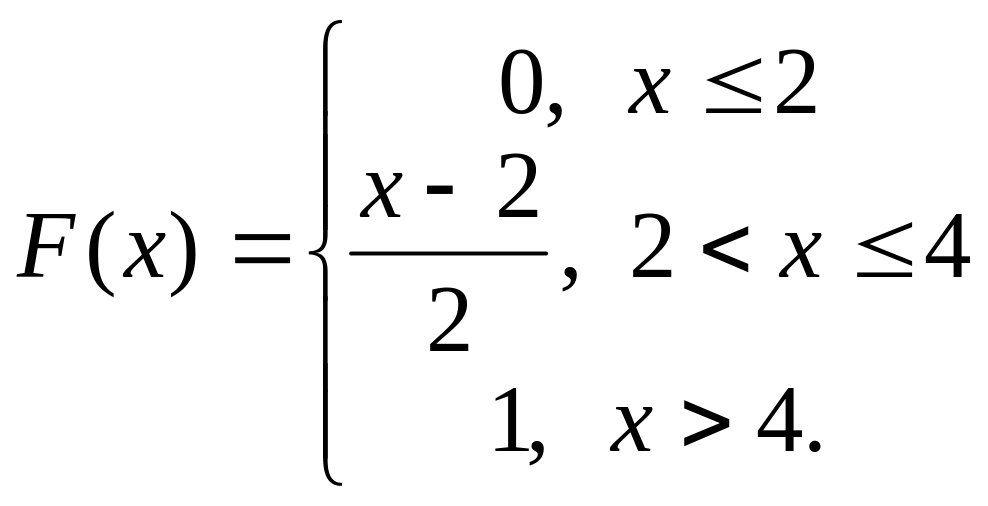
Найти плотность распределения.
Решение. По определению плотность распределения есть первая производная от функции распределения:
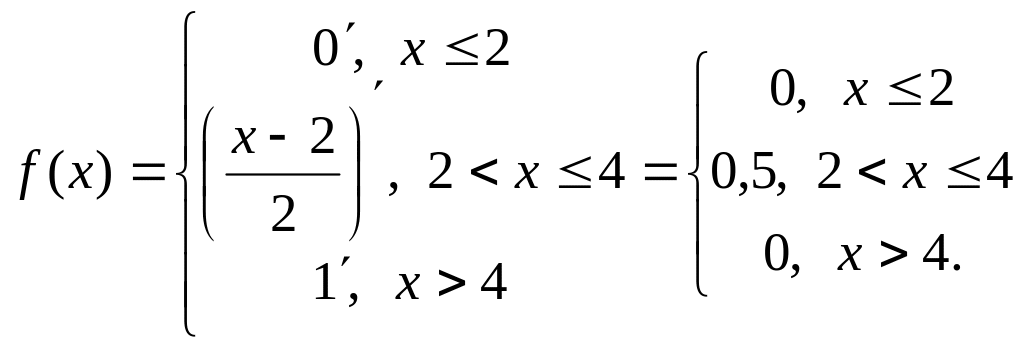
Термин “распределение” для непрерывных случайных величин означает либо функцию распределения, либо плотность распределения вероятностей. Самыми распространенными распределениями непрерывных случайных величин являются равномерное, экспоненциальное и нормальное.
Равномерный закон распределения.
Примером вероятностной модели, в которой появляется равномерное распределение, является бросание точки наудачу на отрезок . Равномерно распределенной в этом случае оказывается координата точки попадания. Плотность равномерного распределения имеет вид:

Вид функции распределения для равномерного распределения:
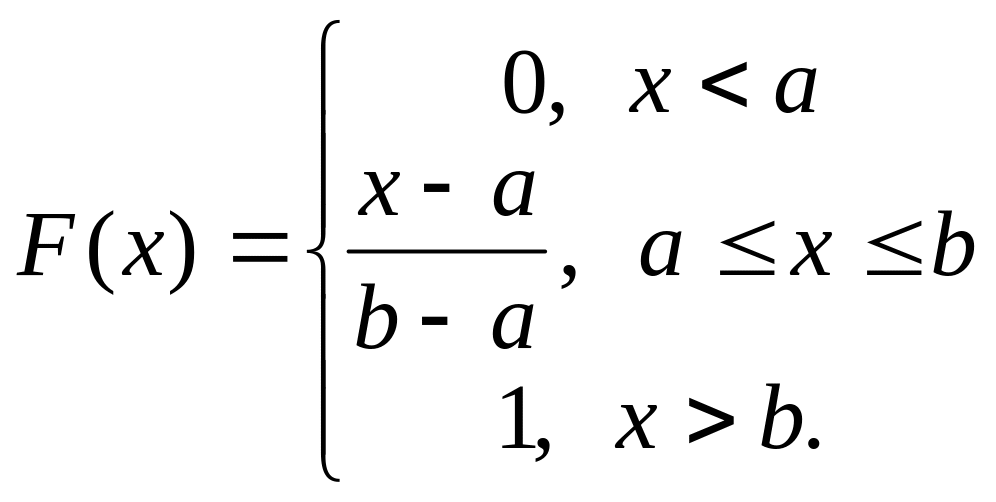
Пример. Автобусы некоторого маршрута идут с интервалом 5 минут. Найти вероятность того, что пришедшему на остановку пассажиру придется ожидать автобуса не более 2 минут.
Решение. Время ожидания является
случайной величиной, равномерно
распределенной в интервале [0, 5]. Тогда
![]()
