5. Щільність (диференціальна функція) розподілу f(X) неперервної випадкової величини х та її властивості.

Диференціальною функцією розподілу або щільністю ймовірностей неперервної випадкової величини Х називають похідну I-го порядку від інтегральної функції F(x):

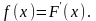
Із формули випливає, що функція розподілу F(x) є первісною для диференціальної функції розподілу f (x).

Теорема. Імовірність того, що неперервна випадкова величина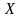 прийме значення з інтервалу , обчислюється за формулою:

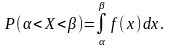
Наслідок. Якщо диференціальна функція розподілу f (x) відома, то інтегральну функцію розподілу F(x) можна знайти за формулою:

Властивості f (x):

1. , тому що вона є похідною зростаючої функції F(x).

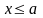2. при та , тому що:

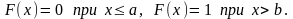
3. тому що подія 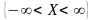є достовірною.

Графік щільності ймовірностей 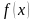називають кривою розподілу.

6. Функція розподілу ймовірностей (інтегральна функція) f(X) випадкової величини х та її властивості.

Інтегральною функцією розподілу (функцією розподілу) називають ймовірність того, що випадкова величина Х прийме значення менше х. Тобто:

F(x) = P(X < x)

Для неперервної ВВ(випадкові величини) Х, мають місце рівності:

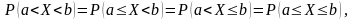
тому що НВВ(неперервні випадкові величини) Х, що приймає значення у проміжку , має незлічену кількість можливих значень набуття Х певних значень 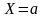або - це майже неможлива подія. Властивості F(x):

1. 1.

2.  Функція 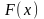неспадна: 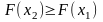, при .

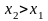3. Для довільних і :

.

4. Якщо можливі значення випадкової величини належать 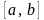, то:

7. Геометричний закон розподілу.

8. Показниковий закон розподілу.

Випадкову величину називають розподіленою за показниковим законом, якщо щільність її імовірностей має вигляд:

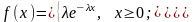
де параметр.

Показниковому розподілу задовільняють: час телефонної розмови, час ремонту техніки, час безвідмовної роботи комп'ютера.

Числові характеристики показникового розподілу:

, .

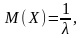
Якщо випадкова величина розподілена за показниковим законом, то її інтегральна функція розподілу має вигляд: 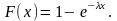Отже, імовірність потрапляння в інтервал 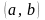буде:

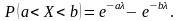
9. Рівномірний закон розподілу.

Величина Х розподілена рівномірно на проміжку (a, b), якщо усі її можливі значення належать цьому проміжку і щільність її імовірностей на цьому проміжку постійна, тобто:

Числові характеристики розподілу:

, .

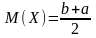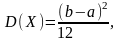
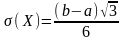10. Біноміальний закон розподілу.

Дискретна випадкова величина ξ називається такою, що маєбіноміальний розподіл, якщо ймовірність набуття нею конкретних значень має вигляд:  , де p, n — параметри, що визначають розподіл,  .

Позначається  .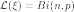

11. Нормальний закон розподілу.

Випадкову величину Х називають розподіленою нормально, якщо щільність її імовірностей має вигляд:

f (х) = , – < x < ,

де а та  - параметри розподілу.

Числові характеристики нормального розподілу:

М (X)= а, ,   (X) = 

Імовірність потрапляння в інтервал нормально розподіленої випадкової величини знаходять за формулою:

де функція Лапласа:

(табульована).