Теоретичні питання з Теорії ймовірностей

1. Випадковий експеримент. Простір елементарних подій. Класичне означення ймовірності випадкової події.

2. Теореми добутку ймовірностей незалежних та залежних подій.

3. Формула повної ймовірності.

4. Числові характеристики випадкових дискретних величин.

5. Щільність (диференціальна функція) розподілу f(x) неперервної випадкової величини Х та її властивості.

6. Функція розподілу ймовірностей (інтегральна функція) F(x) випадкової величини Х та її властивості.

7. Геометричний закон розподілу.

8. Показниковий закон розподілу.

9. Рівномірний закон розподілу.

10. Біноміальний закон розподілу.

11. Нормальний закон розподілу.

12. Незалежні повторювані випробування. Формула Бернуллі.

13. Локальна теорема Лапласа.

14. Інтегральна теорема Лапласа.

15. Формула Пуассона.

16. Первинна обробка та графічне представлення вибіркових даних.

17. Варіаційний ряд розподілу випадкової величини Х.

18. Вибірковий метод.

19. Мода дискретного статистичного розподілу.

20. Варіаційний ряд. Вибіркове середнє та вибіркова дисперсія.

Відповіді:

1. Випадковий експеримент. Простір елементарних подій. Класичне означення ймовірності випадкової події.

Випадковий експеримент (випадкове випробування, випадковий досвід) - математична модель відповідного реальногоексперименту, результат якого неможливо точно передбачити. Математична модель повинна задовольняти вимогам:

• вона повинна бути адекватна і адекватно описувати експеримент

• повинна бути визначена сукупність безлічі спостережуваних результатів в рамках розглянутої математичної моделі при строго певних фіксованих початкових даних, що описуються в рамках математичної моделі.

• повинна існувати принципова можливість здійснення експерименту з випадковим результатом наскільки угодне кількість разів при незмінних вхідних даних ( 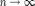  , Де   - Кількість вироблених експериментів).

• повинно бути доведено вимогу або спочатку прийнята гіпотеза про стохастичною стійкості відносної частоти для будь-якого спостережуваного результату, визначеного в рамках математичної моделі:

 , Причому 

 - Спостережуваний результат.

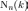 - відносна частота реалізацій експерименту.

Простір елементарних подій — множина всіх можливих наслідків стохастичного експерименту. Тобто, множина елементарних подій. Зазвичай позначаєтеся літерою Ω, також S або U.

В аксіоматичному підході Колмогорова простір елементарних подій є базою ймовірнісного простору. Від природи простору елементарних подій залежить якими будуть випадкові величини на цьому просторі (неперервними чи дискретними).

Простір елементарних подій називається дискретним, якщо множина Ω скінченна або зліченна.

Довільна підмножина простору елементарних подій є подією, всі вони утворюють алгебру подій.

Класичною імовірністю випадкової події А називається відношення кількості елементарних подій m, які сприяють появі цієї події (становлять множину її елементарних подій), до загальної кількості n : P(A)= m /n.рівноможливих елементарних подій, що утворюють простір елементарних подій