4.2. Критерий устойчивости Найквиста.

Найдём выражение для передаточной функции по петле обратной связи первого звена фильтра.

Д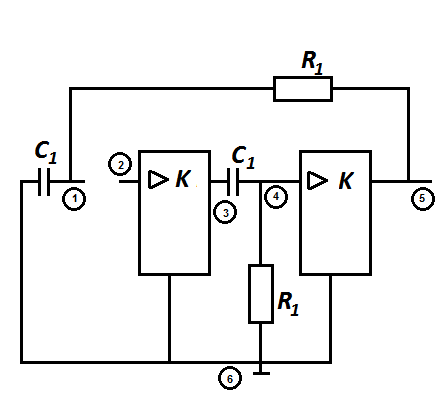 ля определения передаточной функции разорвем цепь обратной связи на входе усилителя и замкнем входные полюса первого звена фильтра. В результате получим схему, приведенную на рис.4.2.

Рис. 4.2.

Представим операционные усилители в виде управляемых источников напряжения и укажем положительное направление узловых напряжений. В результате получим расчётную схему, изображенную на рис. 4.3.

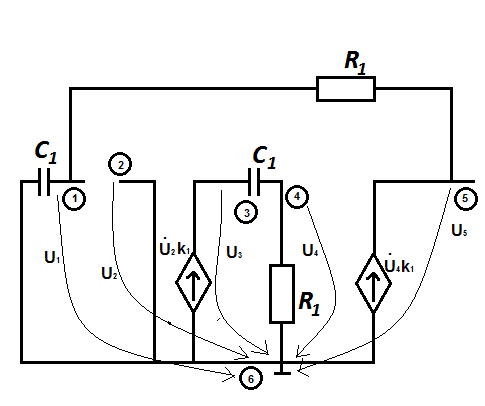
Рис.4.3.

4.2.1.Узловые уравнения схемы в общем виде.

Выберем узел №6 в качестве опорного узла. Тогда В. Составим в комплексной форме узловые уравнения для узлов 1 и 4:

Узел №1:

(4.3)

Узел №4:

_(4.4)

Для данной схемы нужно составить два уравнения связи:

(4.5)

(4.6)

4.2.2.Расчёт коэффициентов левой части уравнений(4.3) и (4.4):

, , , , ,

, , , , .

4.2.3.Расчёт правой части уравнений:

, .

4.2.4.Уравнения (4.3) – (4.6) с учетом найденных коэффициентов:

(4.7)

(4.8)

(4.9)

(4.10)

4.2.5.Решение уравнений (4.7)-(4.10).

Из уравнения (4.7) выразим и сразу подставим (4.10):

, (4.11)

Из уравнения (4.8) выразим . С учетом (4.9) получим:

, (4.12)

Уравнение (4.12) подставим в (4.11) и выразим через :

(4.13)

В результате решения уравнений найдем комплексную передаточную функцию по петле обратной связи:

(4.14)

С помощью среды Mathcad построим годограф по петле обратной связи первого звена фильтра (рис. 4.4.). Исходные данные:

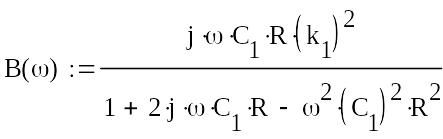
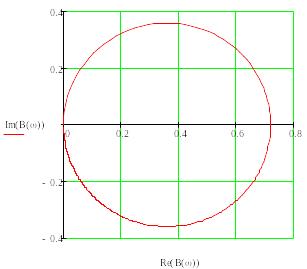
Рис. 4.4.

Поскольку годограф не охватывает точку (1; j0), то по критерию Найквиста данная цепь устойчива.

4.3 Расчёт коэффициента усиления на границе устойчивости.

Максимум передаточной функции приходиться на частоту :

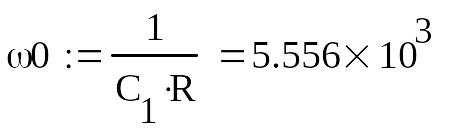
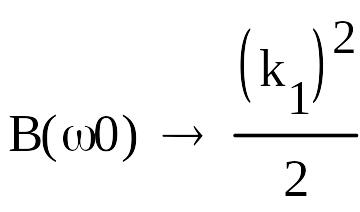
Из этого следует, что для устойчивости цепи коэффициент усиления должен быть . Если , то система будет находиться на границе устойчивости, при этом частота свободных колебаний будет .