3.1 Расчёт допустимой величины ступенчатого воздействия на входе фильтра.
Допустимая величина ступенчатого воздействия равна:
, (3.2)
где
- заданное ограничение по напряжению
на входе второго звена;
–
максимальное
значение
.
Оценим допустимую величину ступенчатого воздействия на фильтр, если напряжение на входе не должно превышать 0.1 В.
В
В
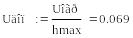
В
Допустимая величина ступенчатого воздействия на фильтр – Uдоп = 0.069 В
Определим основные характеристики динамического процесса при действии на фильтр единичной ступенчатой функции напряжения.
Значения характеристик, полученные по графику.
а) период свободных колебаний –Тсв = 1.42·10-3 - 0.25·10-3 = 1.17·10-3 с
б) частота свободных колебаний –ωсв = 2π / Тсв = 5,370·103Гц
в) затухание – ∆ = 0.55 / 0.10 = 5.5
г) логарифмический декремент затухания – ln(∆) = 1.7
Значения характеристик, полученные путём расчёта:
а) период свободных колебаний –
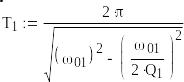
Т1
= 1.178×10
сек
б) частота свободных
колебаний –
=
Гц
в) затухание
-
= Δ , следовательно Δ = 6.25
г) логарифмический
декремент затухания –
= 1.833
Вывод: данные полученные из графика и в результате расчета отличаются незначительно.
Допустимая величина ступенчатого воздействия на фильтр Uдоп = 0.069 В
4. Исследование устойчивости электрического фильтра.
В данной работе анализ устойчивости производится для фильтра и дополнительно для первого звена.
Устойчивость фильтра исследуется по расположению корней характеристического полинома или полюсов передаточной функции цепи на комплексной плоскости. Устойчивость режима работы первого звена следует определить с применением частотного критерия Найквиста.
Рассмотрим оба подхода к определению устойчивости рассматриваемой электрической цепи.
4.1.Определение устойчивости фильтра по расположению полюсов его передаточной функции.
Для определения полюсов передаточной функции необходимо характеристический полином передаточной функции каждого звена фильтра
приравнять к нулю и найти их корни.
Знаменатель передаточной функции первого звена фильтра (1.14) приравняем к нулю и решим полученное уравнение.
(4.1)
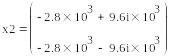
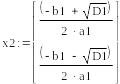
Знаменатель передаточной функции второго звена фильтра (1.24) приравняем к нулю и решим полученное уравнение.
(4.2)
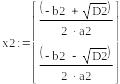
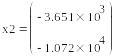
Все полюса расположены в левой полуплоскости комплексной плоскости. Следовательно, данная электрическая цепь устойчива. Расположение корней характеристического полинома на комплексной плоскости представлено на рис. 4.1.
Рис.4.1.