1.2. Расчет передаточной функции второго звена электрического фильтра.
Принципиальная схема электрической цепи звена представлена на рис.1.3.
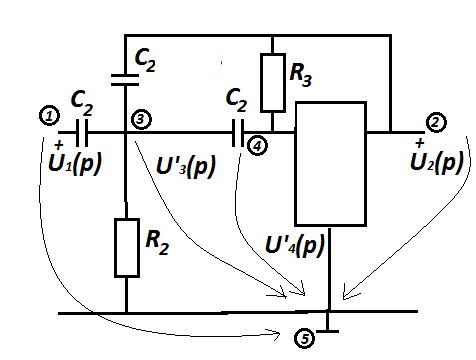
Рис.1.3
Представим схему замещения второго звена (рис. 1.4).
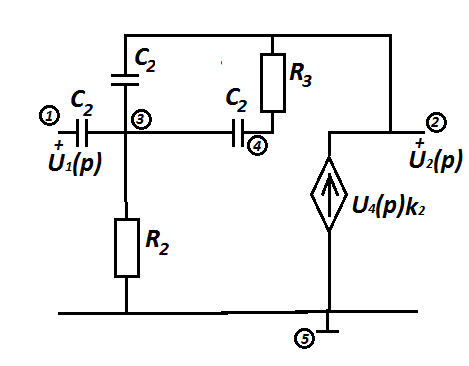
Рис.1.4
2.2.1.Узловые уравнения 2-го звена в общем виде.
Выберем узел 5 в качестве опорного узла. Тогда U’5(p) = U’0(p)=0.
Для расчета передаточной функции достаточно записать уравнения для узлов (3) и (4):
Узел №3:
(1.15)
Узел №4:
(1.16)
Тогда
,
потому что k2
= ∞
(1.17)
2.2.2.Расчёт коэффициентов левой части уравнений (1.15) и (1.16).
,
,
,
,
,
,
,
.
2.2.3.Расчёт правой части уравнений.
,
2.2.4.Уравнения (1.15) – (1.17) с учетом найденных коэффициентов.
(1.18)
(1.19)
(1.20)
2.2.5. Расчет передаточной функции второго звена.
Из уравнения
(1.19) выразим
:
,
(1.21)
Уравнения (1.21)
подставим в (1.18) и выразим
через
:
(1.22)
В результате решения уравнений найдем передаточную функцию звена:
,
(1.23)
Преобразуем
выражение для передаточной функции. С
этой целью разделим числитель и
знаменатель на коэффициент
при
операторе
:
(1.24)
Добротность и частота полюса:
,
1.3. Расчет операторной передаточной функции электрического фильтра.
Передаточная функция фильтра при каскадном соединении звеньев:
(1.25)
2. Расчетные выражения и графики ачх и фчх передаточных функций фильтра.
Расчётные выражения
для частотных характеристик АЧХ и ФЧХ
фильтра получим путём подстановки
в выражение
(1.25). Обе зависимости, построенные в
широком диапазоне частот, определяют
характер преобразования сигнала и тип
фильтра.
2.1. Ачх и фчх передаточной функции первого звена фильтра.
Выражения для комплексной передаточной функции первого звена фильтра получим на основании (1.14), подставив в него :
(2.1)
Учитывая, что
,
выражение (2.1) примет следующий вид:
,
Умножив числитель и знаменатель дроби на сопряженное знаменателю, получим:
Выражение для АЧХ примет вид:
Выражение для ФЧХ:
Построим графики АЧХ и ФЧХ с помощью графического редактора Mathcad. Для этого представим (2.1) функцией аргумента ω :
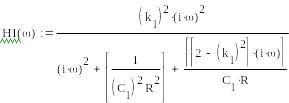
Графики АЧХ передаточной функции первого звена приведены на рис. 2.1 и на рис. 2.2 соответственно в линейном и логарифмическом масштабах.
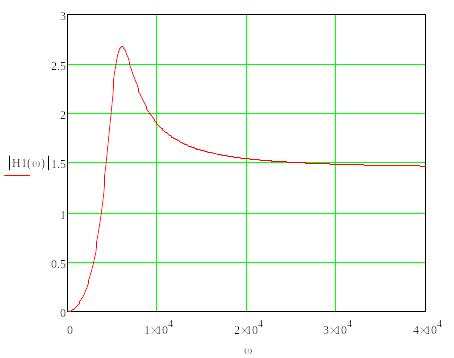
Рис.2.1
График ФЧХ передаточной функции первого звена:
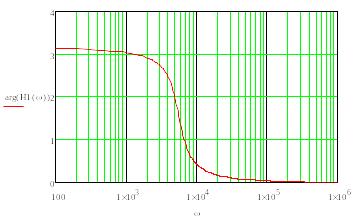
Рис.2.3