Статистики критерия
|
Удовлетворённость работой |
Хи-квадрат |
9,538 |
ст.св. |
4 |
Асимпт. знч. |
,049 |
Заметим, что если анализируемая переменная является бинарной (принимает только два значения — 0 и 1), то можно применить биномиальный критерий через пункт меню Анализ \ Непараметрические критерии \ Биномиальный…
Угловое преобразование Фишера
Рассмотренные ранее критерии довольно легко рассчитываются в статистических пакетах. Однако если этих и подобных им программ под рукой не имеется, то критерии придётся рассчитывать вручную, причём процедура расчёта для каждого критерия своя. Это не очень выгодно в том случае, когда необходимо быстро получить информацию о различиях в уровне исследуемого признака и совсем неудобно для неспециалиста в данной области, вынужденного периодически обращаться к математическим методам для решения указанной проблемы.
Угловое преобразование Фишера φ* является многофункциональным критерием. Он позволяет решать задачи сопоставления уровней исследуемого признака, сдвигов в значениях исследуемого признака и сравнения распределений.
В пользу изучения критерия Фишера φ* говорит также тот факт, что иногда такие критерии как Q-критерий Розенбаума, U-критерий Манна–Уитни, критерий знаков G оказываются не в состоянии выявить искомые различия. В таких случаях исследователю всё равно придётся обращаться к угловому преобразованию Фишера.
Некоторое неудобство для исследователя-гуманитария представляет тот факт, что данный критерий не имеет поддержки в статистических пакетах и соответствующий функции в MS Excel, поэтому вычисление данного критерия производится непосредственно по формуле. Однако выполнив вычисления один раз, в дальнейшем можно только подставлять новые исходные данные и получать результат.
Критерий φ* Фишера предназначен для сопоставления различий между процентными долями двух выборок, в которых зарегистрирован интересующий нас эффект. Формулируются гипотезы:
H0: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 не больше, чем в выборке 2.
H1: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 больше, чем в выборке 2.
Вычисляется эмпирическое значение φ* по формуле:
где ni — общее количество человек в i-ой выборке;
Ni — количество человек в i-ой выборке, у которых проявился исследуемый эффект;
Pi — процентная доля, выраженная в долях единицы.
Полученное эмпирическое значение φ* сравнивается с критическим:
Если
,
то гипотеза Н0
отвергается. При этом необходимо указать
уровень значимости различий (Таблица 10 .4).
Таблица 10.4
Уровни статистической значимости разных значений критерия φ* Фишера2
ρ равно или меньше |
ρ равно или меньше (последний десятичный знак) |
|||||||||
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0,00 |
2,91 |
2,81 |
2,70 |
2,62 |
2,55 |
2,49 |
2,44 |
2,39 |
2,35 |
2,33 |
0,01 |
2,31 |
2,28 |
2,25 |
2,22 |
2,19 |
2,16 |
2,14 |
2,11 |
2,09 |
2,07 |
0,02 |
2,05 |
2,03 |
2,01 |
1,99 |
1,97 |
1,96 |
1,94 |
1,92 |
1,91 |
1,89 |
0,03 |
1,88 |
1,86 |
1,85 |
1,84 |
1,82 |
1,81 |
1,80 |
1,79 |
1,77 |
1,76 |
0,04 |
1,75 |
1,74 |
1,73 |
1,72 |
1,71 |
1,70 |
1,68 |
1,67 |
1,66 |
1,65 |
0,05 |
1,64 |
1,64 |
1,63 |
1,62 |
1,61 |
1,60 |
1,59 |
1,58 |
1,57 |
1,56 |
0,06 |
1,56 |
1,55 |
1,54 |
1,53 |
1,52 |
1,52 |
1,51 |
1,50 |
1,49 |
1,48 |
0,07 |
1,48 |
1,47 |
1,46 |
1,46 |
1,45 |
1,44 |
1,43 |
1,43 |
1,42 |
1,41 |
0,08 |
1,41 |
1,4 |
1,39 |
1,39 |
1,38 |
1,37 |
1,37 |
1,36 |
1,36 |
1,35 |
0,09 |
1,34 |
1,34 |
1,33 |
1,32 |
1,32 |
1,31 |
1,31 |
1,30 |
1,30 |
1,29 |
0,10 |
1,29 |
|
|
|
|
|
|
|
|
|
Ограничения критерия φ*
Ни одна из сопоставляемых долей не должна быть равной нулю.
Верхний предел в критерии φ отсутствует — выборки могут быть сколь угодно большими.
Нижний предел — 2 наблюдения в одной из выборок. Однако должны соблюдаться следующие соотношения в численности двух выборок:
если в одной выборке всего 2 наблюдения, то во второй должно быть не менее 30: n1=2 → n2≥30;
n1=3 → n2≥7;
n1=4 → n2≥5;
при n1,n2≥5 возможны любые сопоставления.
Задача 10.23. Допустим, нас интересует, различаются ли две группы студентов по успешности решения новой экспериментальной задачи. В первой группе из 20 человек с нею справились 12 человек (60%), а во второй выборке из 25 человек — 10 (40%). Можем ли мы утверждать, что в первой группе результат значительно выше, чем во второй? Сформулируем гипотезы.
H0: Доля лиц, справившихся с задачей, в первой группе не больше, чем во второй группе.
H1: Доля лиц, справившихся с задачей, в первой группе больше, чем во второй группе.
Как уже отмечалось, решение проводится в MS Excel.
Озаглавить ячейки A2 и A3 как 1 группа и 2 группа соответственно.
Озаглавить ячейки B1 и C1 как n и N соответственно.
Ввести исходные данные (Рис. 10 .3).
В ячейках D2 и D3 вычислить φi по формулам =2*ASIN(КОРЕНЬ(C2\B2)) и =2*ASIN(КОРЕНЬ(C3\B3)) соответственно.
В ячейке E2 вычислить значение φ* по формуле =ABS(D2-D3)*КОРЕНЬ(B2*B3\(B2+B3)).
В ячейке F2 оформить вывод значимости различий с помощью вложенной функции:
=ЕСЛИ(E2<1,64;"Различия незначимы";ЕСЛИ(E2>=2,31;"Различия значимы";"Зона неопределённости")).
Рис. 10.3. Вычисление критерия Фишера φ* в MS Excel
Как видно, полученное эмпирическое значение φ*=1,34 находится в зоне незначимости (Рис. 10 .4). Принимается гипотеза H0.
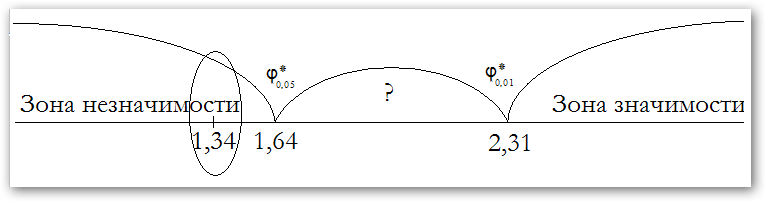
Рис. 10.4. Ось значимости для критерия Фишера φ*
1 За основу взята задача: Ермолаев О. Ю. Математическая статистика для психологов: Учебник. — 2-е изд., испр. — М.: Московский психолого-социальный институт: Флинта, 2003. С. 130.
2 Подобные таблицы содержатся в приложениях ко всем справочным и учебным пособиям по методам статистической обработки данных.
3 Сидоренко Е. В. Методы математической обработки в психологии. — СПб.: Речь, 2003. С. 161.