18

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ЭНЕРГЕТИЧЕСКИЙ УНИВЕРСИТЕТ

_________________________________________________________

кафедра ТОЭ

Дисциплина «Метрология, стандартизация и сертификация»

Раздел 2

«Погрешности измерений и обработка результатов измерений»

Лекция 5

«Обработка результатов измерения»

Распределение времени:

1. Вводная часть (объявление темы, цели и вопросов лекции) ……. 3 мин.

2. Основная часть (рассмотрение учебных вопросов)……………...80 мин.

2.1. Технические (однократные) измерения…........………...30 мин.

2.2. Многократные равноточные измерения………………..30 мин.

2.3. Многократные неравноточные измерения………………20 мин.

3. Заключительная часть(общие замечания, контроль присутствия) 7 мин.

Автор:

Рассмотрена и утверждена на заседании ПМК «__»___2007 г. Протокол №

КАЗАНЬ 2007

1. Вводная часть

В целях повышения психологического настроя студентов на восприятие данной дисциплины в начале каждой лекции целесообразно проводить короткий опрос по материалу предыдущей лекции.

Вопросы для контроля:

а) Что понимается под погрешностью ?

б) Перечислите виды погрешностей.

в) Назовите причины возникновения погрешеостей.

Требовать от отвечающих студентов представления перед ответом по форме: «Студент Сергеев. Группа ЭП – 1 – 04». Оценки заносить в журнал преподавателя.

После опроса объявить тему и цель лекции.

2. Основная часть

2.1. Технические (однократные) измерения

Измерения с однократными наблюдениями встречаются значительно чаще, чем многократные, особенно на производстве. Простота, низкая трудоемкость, возможность проведения большого количества измерений в единицу времени, низкая стоимость, во многих случаях достаточная точность являются важными достоинствами однократных измерений. В некоторых случаях проведение многократных измерений нецелесообразно из-за экономических соображений, в некоторых случаях они невозможны из-за разрушения объекта измерения в процессе самого измерения.

Результат единственного отсчета показания средства измерения содержит как систематические, так и случайные составляющие погрешности. Особенностью однократного измерения является то, что законы распределений случайных составляющих погрешностей неизвестны и представление о них формируется на основе ограниченной априорной информации, а иногда и на основе интуиции.

Проведение однократных измерений возможно, если средства измерений прошли поверку, метрологически аттестованы, соответствуют своему классу точности, метод измерения достаточно апробирован, и производят их обычно тогда, когда случайными составляющими по­грешностей можно пренебречь по сравнению с неисключенными остатками систематических погрешностей. Поверкой называется определение метрологическим органом погрешностей средства измерения и установление средства измерения к применению. Поверка осуществляется в соответствии с требованиями, устанавливаемыми в нормативно-технической документации на средство измерения. Результаты поверки указываются в свидетельстве о поверке или паспорте на средство измерения.

Согласно методике МИ 1552-86 "ГСИ. Измерения прямые одно­крат­ные. Оценивание погрешностей результатов измерений" требуется, чтобы составляющие погрешности были определены. Причем принимается, что случайные составляющие распределены по нормальному закону, а неисключенные остатки систематических погрешностей по равномерному закону с указанием границ.

Полагают, что погрешность измерений  складывается из следующих составляющих: основной, дополнительной, взаимодействия, динамической.

· Основная погрешность _о  погрешность средства измерения при нормальных условиях проведения измерения. Основной вклад в основную погрешность вносит инструментальная погрешности _и, которая является следствием несовершенства конструкции и технологии изготовления, износа и старения средства измерения.

· Суммарная дополнительная погрешность _д определяется классом точ­­ности средства измерения и различными влияющими величинами. Состоит из ряда составляющих:

 погрешности от неправильной установки _уст  наклон прибора, близкое расположение однотипных приборов и т.д.;

 погрешности от внешних воздействий  температуры, давления, влажности, электрических и магнитных полей, вибраций и т.д.

 методической погрешности _м, связанной с несовершенством метода измерения, использованием идеальной функциональной зависимости вместо реальной;

 погрешности отсчитывания _отс. В приборах с цифровым отсчетным устройством _отс не превышает одного кванта шкалы и обычно включается в состав основной погрешности. Для аналоговых приборов предельное значение _отс.п зависит от доли округления при отсчете и от цены деления шкалы:

(5.1)

где Ц  цена деления; k  коэффициент, значение которо­го зависит от долей округления. Фактически k определяется погрешностями, вносимыми экспериментато­ром при отсчете (погрешностями от округления, интерполя­ции, параллакса); практически этот коэффициент может принимать значения от 0,1 до 0,5;

 погрешности вычислений _выч  погрешности от округлений про­ме­жу­точных результатов измерений;

 субъективные погрешности  это погрешности, связанные с индивидуальными особенностями наблюдателя, его квалификацией, внимательностью и скоростью работы.

· Динамическая составляющая погрешности измерений _дин прояв­ляется при изменении значений измеряемых физических величин. Любое средство измерения обладает инерцией (электрической, тепловой, механической и т.п.), поэтому не может мгновенно реагировать на изменение измеряемой физической величины. Следовательно, при измерении изменяющейся во времени величины в каждый момент времени будет наблюдаться некоторое отставание показаний средства измерения от истинного значения физической величины. Динамическая погрешность зависит от динамических свойств средств измерения. При статических измерениях, когда скорость изменения измеряемой физической величины пренебрежимо мала, данная составляющая погрешности может не учитывается.

· Причина появления погрешности взаимодействия СИ с объектом измерения _вз обусловлена неидеальностью внутреннего сопротивления средства измерения. При включении средств измерений, обладающих конечными значениями внутренних сопротивлений, в измеряемой цепи может произойти изменение режимов ее работы.

Известно, что при измерении напряжения в цепях постоянного тока с помощью вольтметра с внутренним сопротивлением R_V возникает погрешность взаимодействия из-за снижения падения напряжения на измеряемом участке цепи. Относительная погрешность при этом рассчитывается по формуле

(5.2)

где R_вых  выходное сопротивление измеряемого участка цепи.

При измерении тока амперметром относительная погрешность взаимодействия равна

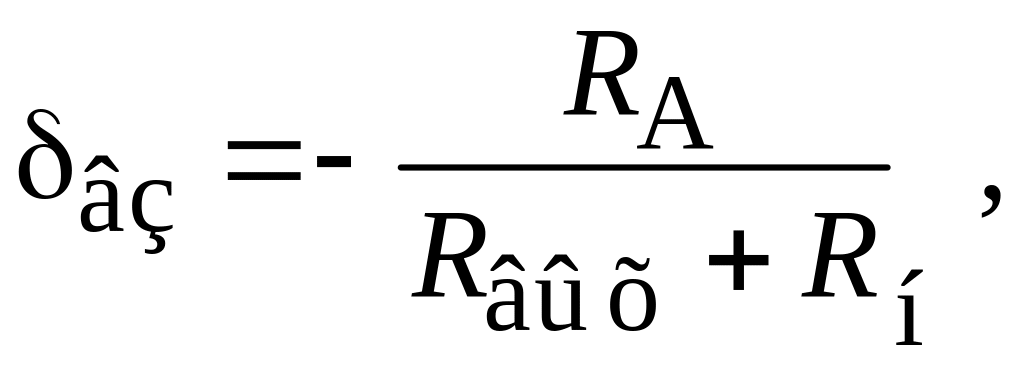
(5.3)

где R_А  внутреннее сопротивление амперметра; R_н  сопротивление нагрузки.

Для средств измерений с указанными значениями входного тока I_вх и входного сопротивления R_вх

(6.4)

При измерении на переменном токе в технической документации на средство измерения обычно указываются значения активного входного сопротивления и параллельно включенной емкости С_вх. В этом случае

(6.5)

где   круговая частота.

При постоянном включении средства измерения в измеряемую цепь, когда средство измерения является элементом измеряемой цепи, погрешность взаимодействия не учитывается.

Ниже приведен порядок определения и учета составляющих систематических погрешностей результата прямого однократного измерения, которого следует придерживаться.

По известным нормируемым метрологическим характеристикам средств измерения можно определить предельные значения некоторых составляющих погрешности измерения _i. Для симметричных составляющих погрешности можно определить предельное значение погрешности результата измерения, просуммировав составляющие:

(6.6)

где m  количество составляющих систематической погрешности.

Для такого случая результат измерения представляется в виде

Х ± ; P = 1. (6.7)

Если пределы хотя бы для одной составляющей погреш­ности результата измерения несимметричны, то модули нижнего и верхнего пределов будут неравны, поэтому необходимо вычислить нижний и верхний пределы погрешности резуль­тата измерения (_н, _в) с учетом их знаков.

Результат измерения при несимметричных пределах погрешности представляется в виде

X;  от _н до _в; Р = 1. (6.8)

В тех случаях, когда возможно найти систематическую составляющую погреш­ности _с (систематическую погрешность) измерения, резуль­тат измерения целесообразно исправить внесением поправки, т.е. вместо значе­ния Х измеренной величины использовать исправленное значение X_испр:

Х_испр = Х - _c , (6.9)

соответственно изменив пределы погрешности измерения:

_испр,н = _н - _с , (6.10)

_испр,в = _в - _с. (6.11)

Так как исправленные пределы погрешности окажутся симметричными относительно нуля, то исправленный результат измерения в этом случае можно представить в виде

Х_испр ± ; P = 1. (6.12)

Систематическую погрешность _с можно найти в случаях, когда пределы хотя бы одной составляющей погрешности имеют один знак или несимметричны относи­тельно нуля при симметричном распределении погрешности относительно середины интервала возможных значений. Пусть, например, составляющая _i погрешности  распреде­лена по закону равномерной плотности в интервале от _i,н до _i,в; тогда систематическая составляющая _i,с этой ча­стной погрешности может быть определена по формуле

_i,с = 0,5(_i,н + _i,в). (6.13)

Напомним, что по нормируемым метрологи­ческим характеристикам можно определить только предель­ные значения _i,п составляющих _i погрешности измерения .

Выше были рассмотрены вопросы обработки резуль­татов однократных измерений для доверительной вероятно­сти Р = 1. Чтобы произвести обработку результатов для заданной доверительной вероятности, отличной от 1, необходимо знать законы распределе­ния частных погрешностей и уметь осуществлять их композицию; при этом реальные законы распределения принято заменять стандартными аппроксимациями.

Так, для неисключенных остатков систематических погрешностей, равно­мерно распределенных в заданных симметричных относительно нуля пределах, при условии, что ни одна частная погрешность явно не пре­обладает в сумме этих погрешностей, границы (±) симметричного доверительного интервала для погрешности результата измерения можно найти по приближенной формуле

(6.14)

где _i  симметричные пределы доверительного интервала при дове­рительной вероятности Р_i для i-й составляющей по­грешности; К  коэффициент, соответствующий выбранной доверительной вероятности Р, зависящий от числа составляющих неисключенной систематической погрешности и их законов распределения. При Р = 90 % К принимается равным 0,95, при Р = 95 % К = 1,1, при Р = 99 % К = 1,4. Для других доверительных вероятностей он может быть определен в соответствии с ГОСТ 8.0207-76.

Для доверительной вероятности, отличной от единицы, при наличии несимметричных составляющих погрешности также следует отдельно определять верхние и нижние границы с представлением результата аналогично (5.8) либо вносить поправку в результат измерения и указывать исправленное предельное значение.

Перед проведением однократного измерения рекомендуется проанализировать априорную информацию об объекте измерения, убедиться в исправности средства измерения, оценить составляющие погрешности.

Пример расчета погрешности технического измерения. При измере­нии тока аналоговым амперметром класса точности 1,5 со шкалой 05 А, содержащей 100 делений, стрелка указателя с округлением до десятых долей показывает 38,2 деления. Температура окружающего воздуха составляет 15 ^оС. Сопротивление нагрузки 1 кОм, выходное сопротивление цепи 500 Ом, входное сопротивление амперметра 25 Ом. Записать результат технического измерения, считая, что точность отсчета составляет половину от минимального деления шкалы.

Решение. Определим цену деления 5/100 = 0,05 А. Отсюда показание амперметра 0,0538,2 = 1,91 А.

Рассмотрим составляющие погрешности.

Так как измерение статическое, динамическая составляющая погрешности отсутствует. Методической погрешностью, погрешностью вычислений, погрешностью от неправильной установки амперметра, дополнительной погрешностью от воздействия электромагнитных полей, давления, влажности и т.д. согласно условиям задачи можно пренебречь.

Таким образом, имеются следующие составляющие погрешности: основная, взаимодействия, отсчета, дополнительная от воздействия температуры. Рассчитаем их значения.

Основная составляющая погрешности может быть рассчитана из класса точности амперметра. Класс точности нормирован по предельной приведенной погрешности 1,5 . С учетом нормирующего значения для данного амперметра I_н = 5 А получаем

_о =  _оI_н/100 =  1,55100 =  0,075 А.

Допустив, что предельное значение погрешности отсчета симметрично и составляет половину от минимального деления шкалы, рассчитаем предельное значение погрешности отсчета:

_отс = 0,50,075 =  0,0375 А.

Определим составляющую дополнительную погрешность от влияния температуры. Известно, что для измерительных приборов класса точности 0,1 область нормальных значений температуры составляет (20  2) ^оС, область рабочих температур (+10  +35) ^оС, причем дополнительная температурная погрешность не превышает основной на каждые 10 ^оС. Поэтому

Рассчитаем погрешность взаимодействия объекта измерения с амперметром _вз. Так как включение амперметра в измеряемую цепь приводит к уменьшению тока через нагрузку, т.е. к снижению показаний амперметра, эта составляющая погрешности отрицательная:

Отсюда при I = 1,9 А

_вз = -1,911,67/100 = -0,031897  -0,032 А.

Просуммируем составляющие погрешности. В связи с тем, что имеется несимметричная составляющая погрешности, вычислим отдельно верхнее и нижнее предельные значения погрешностей измерений:

_в = _о + _отс + _д = 0,075 + 0,0375 + 0,0375 = 0,15 А.

_н = -(_о + _отс + _д + _вз) = -(0,075 + 0,0375 + 0,0375 + 0,032) =

= -0,182  -0,18 А.

Результат измерения, согласно (5.8), можно представить в виде

1,91 А;  от - 0,18 А до 0,15 А; Р = 1.

Результат измерения можно представить и в виде (5.12), если внести поправку в результат измерения. В данной задаче имеется лишь одна несимметричная составляющая погрешности  взаимодействия. В соответствии с (5.13)

_вз,с = 0,5(0,032 + 0) = 0,016.

Исправленный результат измерения: 1,91 + 0,016 = 1,926  1,93 А.

Определим предельную погрешность исправленного результата:

 = _о + _отс + _д + _вз,с = 0,075 + 0,0375 + 0,0375 + 0,016 = 0,166  0,17 А.

Результат измерения, согласно (5.12),

(1,93  0,17) А; Р = 1.