5 Эквивалентные операторные схемы
При расчете п.п. операторным методом желательно сразу записывать уравнения Кирхгофа в операторной форме, а также уравнения с применением известных методов.
Любую систему уравнений можно записать, составив для заданной схемы эквивалентную операторную схему.
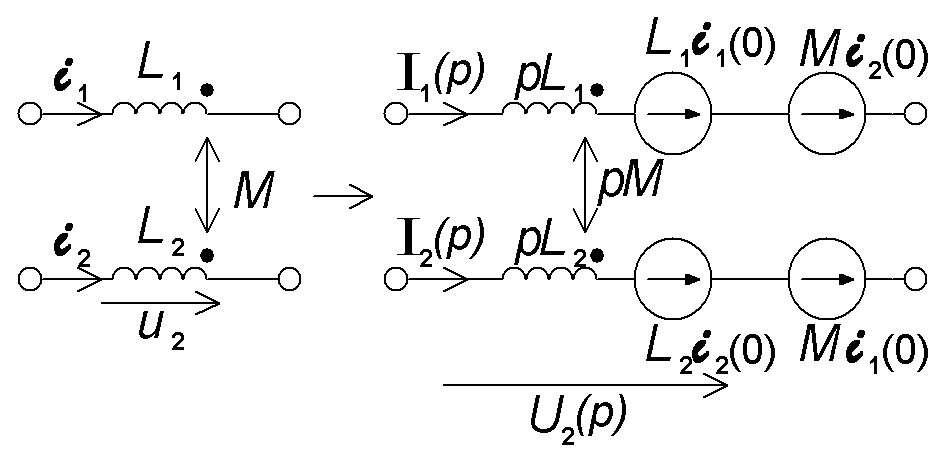
6 Расчет цепей операторным методом
Порядок расчета
1 Операторное
сопротивление записывается как и
сопротивление в комплексной форме,
заменяя
на
.
2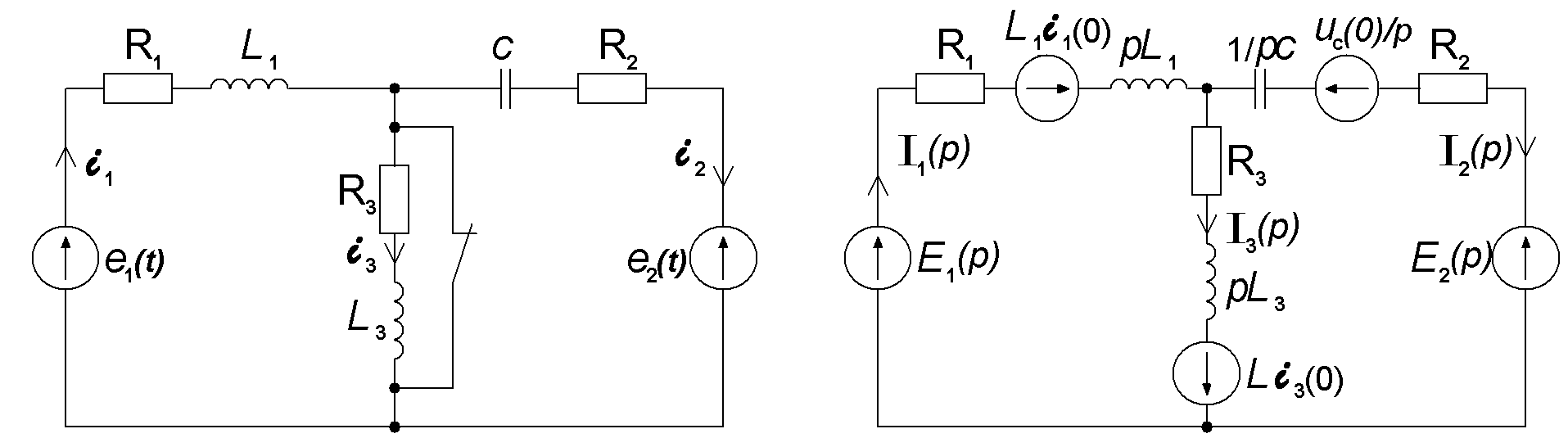
Уравнения для изображений тока и
напряжения могут быть получены по любым
известным методам для операторной схемы
замещения
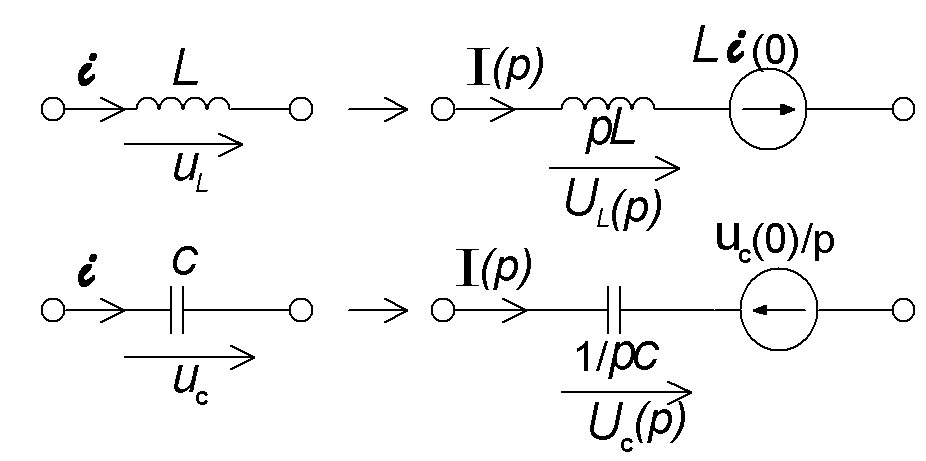
При ее составлении все переменные величины заменяются операторными изображениями:
Индуктивности
заменяется последовательными схемами,
составленными из операторного
сопротивления
и источника ЭДС
,
имеющего направление, совпадающее с
током. Емкость заменяется последовательной
схемой с операторным сопротивлениям
и источником ЭДС
,
направленным против напряжения на
емкости.
7 Формулы соответствия
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
.
8 Нахождение оригинала по изображению с помощью обратного преобразования Лапласа
Переход от изображения к функции времени может быть осуществлен тремя путями:
1. С помощью формул
соответствия (из таблиц). Формулами
соответствия рекомендуется пользоваться
в том случае, если среди корней уравнения
есть кратные корни.
2. Состоит в применении формулы разложении
3. Непосредственное применение формулы обратного преобразования Лапласа с использованием теории вычетов.
Второй путь получил наибольшее распространение.
1 Разложение сложной дроби на простые
Из курса математики известно, что дробь
,
Если
и
не имеет кратных корней, может быть
представлена в виде суммы простых дробей
.
или
,
где
корни
уравнения
.
.
Таким образом:
.
.
Пример:
.
.
;
.
2 Формула разложения
Переход от
изображения
к функции времени производят с помощью
формулы
формула
разложения.
При этом
.
Изображение,
например, тока
заменим
в виде простых дробей:
.
Оригиналом будет
являться
равен
сумме оригиналов слагаемых
,
при этом число слагаемых равно числу корней.
Если среди корней
есть нулевой корень
,
то
,
где
представляет составляющую искомого
тока, обусловленную постоянными
вынуждающими силами. Если постоянных
вынуждающих сил в схеме нет, то
.
Замечания к формуле разложения
1) Формула разложения
применима при любых н.у. и любых формах
2) Если н.у. ненулевые,
то в
войдут внутренние ЭДС.
3) Если имеет комплексно-сопряженные корни, то слагаемые в формуле разложения оказываются также комплексно-сопряженными и в сумме дают действительное слагаемое.
4) Если воздействующая
на схему ЭДС синусоидальна
и изображение ее
,
то при использовании формулы разложения
из ее правой части для перехода от
комплекса к мгновенному значению следует
взять коэффициент при j
( мнимая часть), т.к.
и есть мнимая часть комплекса
.
Внутренние ЭДС, которые появляются при
ненулевых н.у. в цепях с синусоидальными
ЭДС, должны быть умножены на j.
В цепях с постоянными ЭДС внутренние ЭДС на j не умножаются.
5) Если воздействующее
на схему напряжение синусоидально, то
принужденная составляющая решения
входит в число слагаемых
и
определяется корнем
.
Для сложных схем вычисление принужденных составляющих громоздко, поэтому в этом случае рекомендуется вычислять ее символическим методом.
6) Если среди корней
имеются комплексно сопряженные корни
,
то для вычисления соответствующих им
слагаемых, в формуле разложения достаточно
определить слагаемые одного из этих
корней
,
а для сопряженного взять сопряженное
полученного значения. Сумма, соответствующая
двум слагаемым, равна удвоенному значению
действительной части.
.
7) Случай кратных
корней. Если в выражении
имеются
различных корней и из них есть корень
кратностью
,
,
то
.
Например
.
3 Обратное преобразование Лапласа (это третий путь).
Для нахождения может быть использовано обратное преобразование Лапласа
.
Функция
аналитична в области в области
и стремиться к нулю при
.
При практическом использовании этой формулы интеграл по бесконечной прямой, параллельной оси ординат, заменяют контурным интегралом, охватывающим все полюса :
.
Полюсом
называется значение p
при которых
обращается в
,
т.е. когда
,
полюсами являются корни уравнения
.
.
Вычетом
функции
в некотором полюсе называют величину,
на которую уменьшаются разделенные на
контурный интеграл от этой функции.
Вычет функции
в
полюсе
равен
.
Поэтому из обратного преобразования
Лапласа выводится формула разложения
.