1 Прямое преобразование Лапласа

Изображение по Лапласу называется функция, которая получается в результате вычисления интеграла

, (*)

если удовлетворяет следующим условиям:

t-вещественная переменная

а) и ее производные-непрерывны (или имеют конечное число разрывов I рода)

б) при t=0.

, или

.

Выражение (*) называют прямым преобразованием Лапласа.

Обратное преобразование Лапласа:

.

2 Основные свойства преобразования Лапласа и изображение простейших функций

К преобразованиям Лапласа применимо свойство линейности.

1) При умножении оригинала на постоянную величину, на ту же величину умножается изображение

2) Изображение суммы функций равно сумме их изображений:

.

Простейшим оригиналами являются единичная и показательная функции.

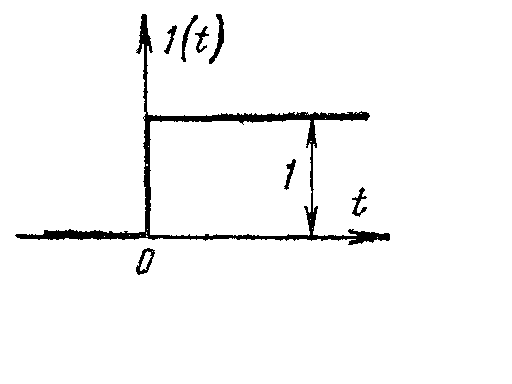
1)

2) Изображение постоянной величины

.

3) Изображение показательной функции: . Тогда ее изображение

.

Итак, .

4. Изображение синусоидальной функции .

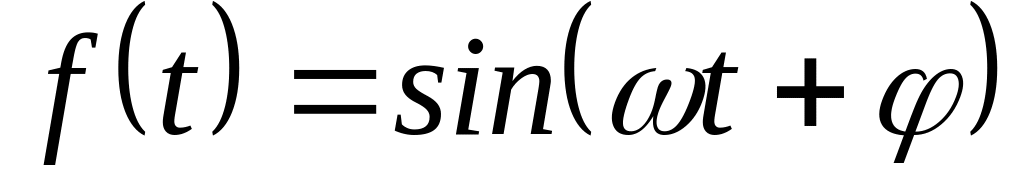Т.к. , то

при .

; при .

Особого внимания заслуживает преобразования, связанные с дифференцированием и интегрированием.

5. Изображение производной

.

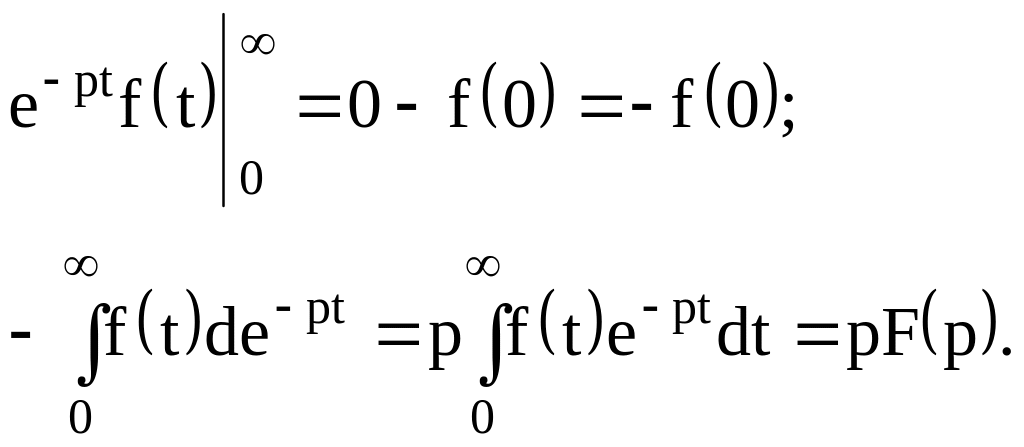
Т.е.

;

, и т.д. Поэтому

,

если , то

.

6. Изображение интеграла 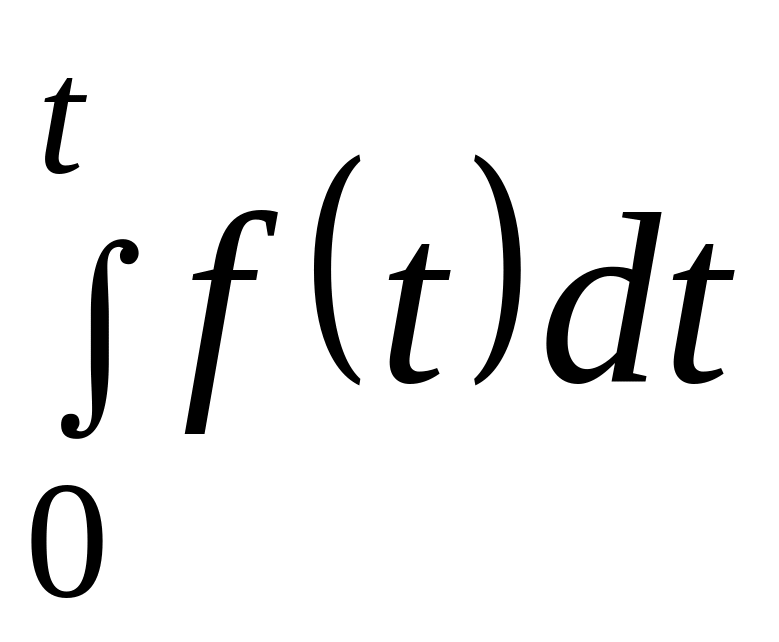, т.е.

Таким образом, .

.

3 Некоторые теоремы и предельные соотношения

1 Теорема смещения в области оригиналов (теорема запаздывания).

Если изображение функции равно , то изображение функции . Теорему легко доказать подставив в преобразование Лапласа:

.

2 Теорема смещения в области изображений

Если , то .

, показывает, как изменяется изображение при умножении оригинала на показательную функцию.

3 Теорема об изменении масштаба (теорема подобия).

Если , то .

Все три теоремы доказываются подстановкой функции в прямое преобразование Лапласа.

4 Нахождение начального значения функции по изображению :

5 Нахождение установившегося значения функции по изображению функции : .

4 Законы электрических цепей в операторной форме

Закон Ома ;

где начальное напряжение на конденсаторе, обусловленное электрическими зарядами в момент коммутации.

Тогда: .

закон Ома в операторной форме.

Или

.

называют полным сопротивлением цепи в операторной форме или операторным сопротивлением. Величина, обратная операторному сопротивлению, называется операторной проводимостью:

.

Операторная ЭДС цепи, состоит не только из операторного изображения ЭДС источника , но из слагаемых, которые определяются начальными условиями и , т.е. внутренними ЭДС, показывающими, что в момент коммутации в магнитном поле катушки и в электрическом поле конденсатора была запасена энергия. Положительное направление ЭДС совпадает с положительным направлением тока ветви, а ЭДС противоположно.

При нулевых н.у.( =0 и =0) закон Ома имеет вид

.

2) Законы Кирхгофа

Первый закон Кирхгофа в операторной форме имеет вид:

,

причем некоторые из токов могут изображением токов источника тока.

Второй закон Кирхгофа

в операторной форме

,

или

,

при нулевых н.у.

.