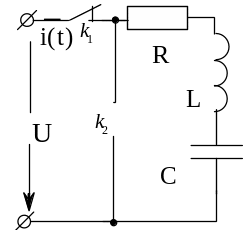
Б) Разряд емкости на r – l цепь

Контакты срабатывают синхронно. Апериодическая разрядка. Начальные условия:

Откуда .

Учитывая, что , получим

.

Т.к. , то

,

.

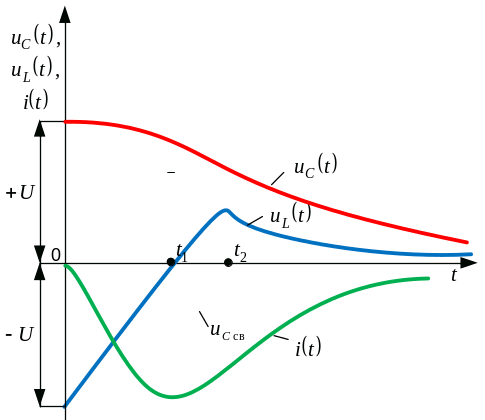
Максимум тока кривой точки перегиба падений напряжений на С и совпадают во времени. Ток начинает изменяться от 0, нарастая до максимального значения. В этот момент времени ЭДС самоиндукции, ранее препятствующая протеканию тока, меняет знак и старается поддерживать ток максимальным. В этот момент проходит через 0 из(-) в (+).

Однако, вследствие того, что в контуре отсутствуют сторонние источники энергии, ЭДС самоиндукции не способна удерживать ток на прежнем уровне и ток уменьшается.

2. Предельный случай разряда емкости на 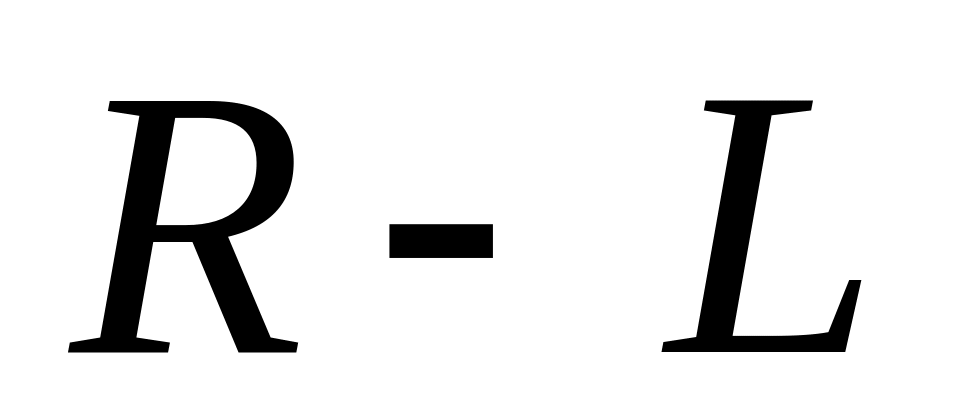цепь

, корни .

В этом случае общее решение имеет вид

.

При , откуда

,

т.е.

,

,

т.к. , получим

,

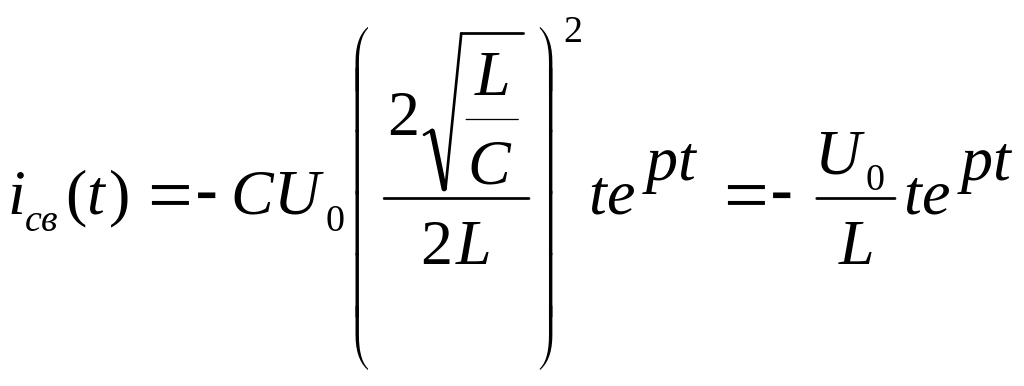Кривые изменения и по форме мало отличаются от случая апериодической разрядки конденсатора.

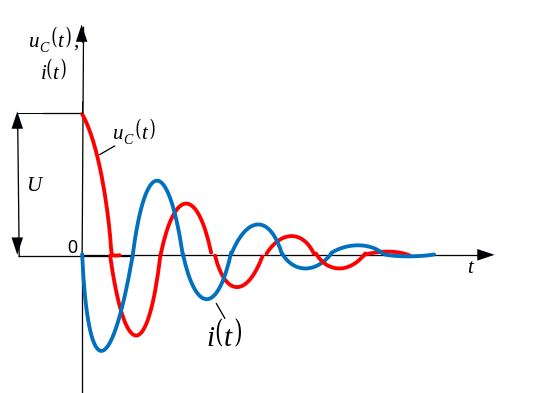
3. Периодическая (колебательная) разрядка конденсатора

Разрядка будет периодической, если

,

где

Решение дифференциального уравнения при комплексно-сопряженных корнях имеет вид:

,

.

При

Определим постоянные интегрирования . При этом

;

.

Обозначив , , получим

При переходе через 0. конденсатор разряжается . Ток и напряжения представляют затухающие колебания с угловой частотой . Причем , и зависят только от параметров .

Быстроту затухания оценивают с помощью декремента затухания

или

логарифмического декремента

.

Если кривая затухает медленно, то отношение ее значения стремится к 1.

Сопротивление оказывает существенное влияние на скорость затухания , кроме этого по мере увеличения уменьшается и увеличивается .

Когда и наступает критический случай. Наоборот, при (идеальный случай) , т.е. затухание процесса равно 0 (первоначальный запас энергии остается неизменным и энергия попеременно переходит из электрического поля в магнитное и наоборот).

В) Включение r – l– c цепи на синусоидальное напряжение

При этом в схеме нулевые н.у., конденсатор с емкостью не заряжен.

г де .

,

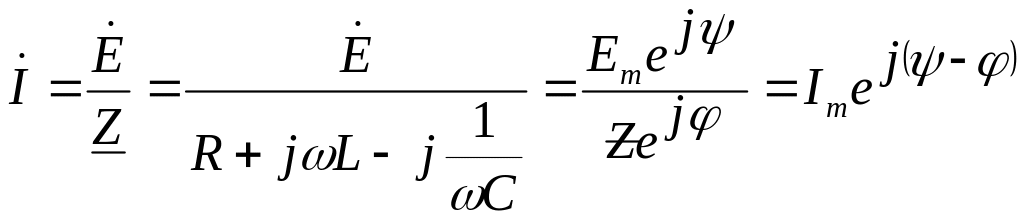где .

,

.

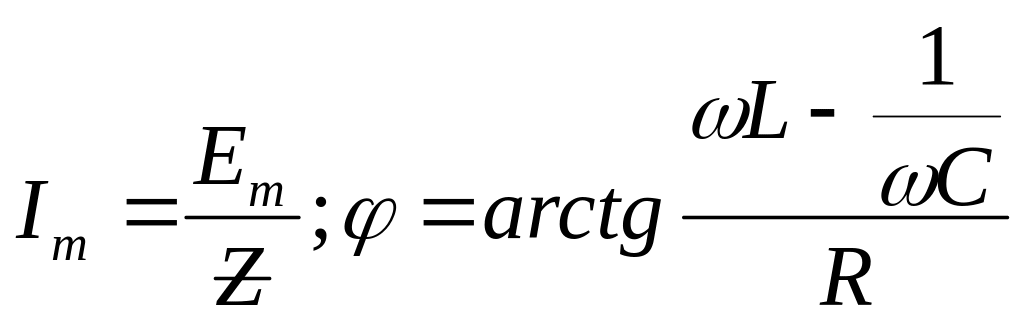1. Апериодический п.п.

Решения для напряжения на конденсаторе и тока в цепи будут иметь вид: ;

.

Т.к. , то

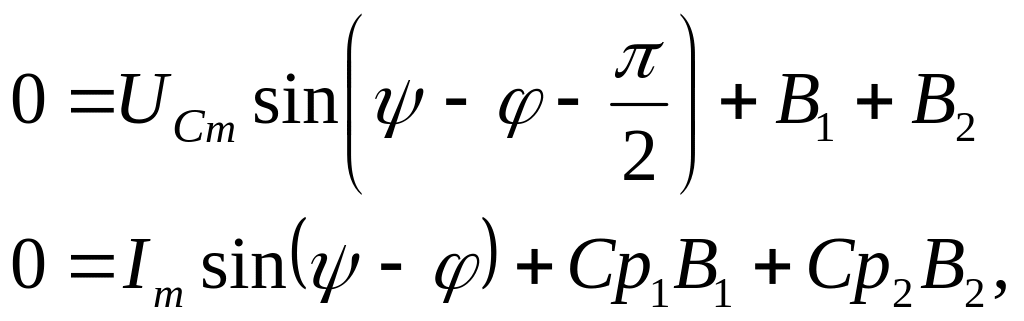
Из первого уравнения выражаем

и подставим во второе уравнение:

откуда постоянная интегрирования:

.

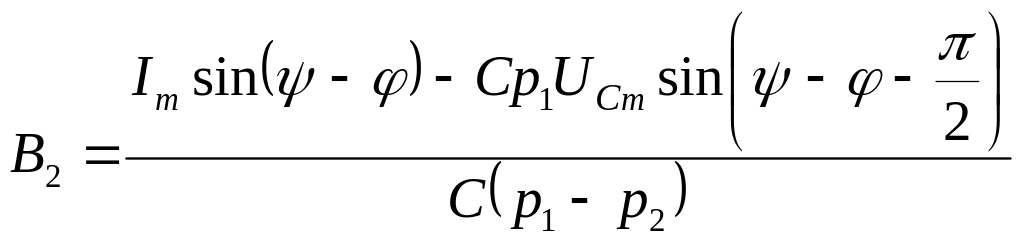Пример графика тока построен для следующих параметров цепи:

100 В, , 180 , 150 Ом, 0,5 Гн, =100 мкФ, ( = ).

2)Колебательный п.п. при .

;

.

Т.к. , то

,

.

Выразив из первого уравнения последней системы

.

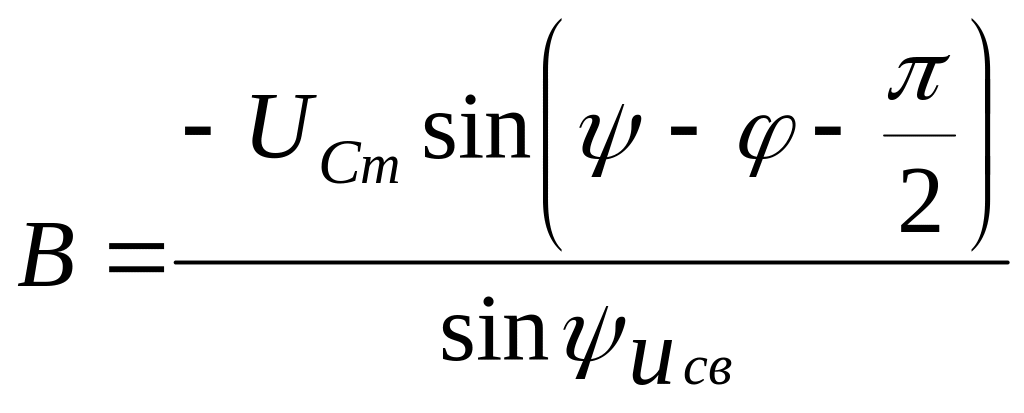И подставив во второе уравнение получим

.

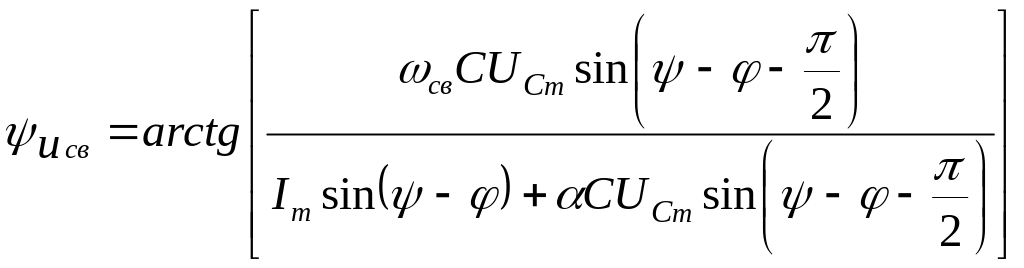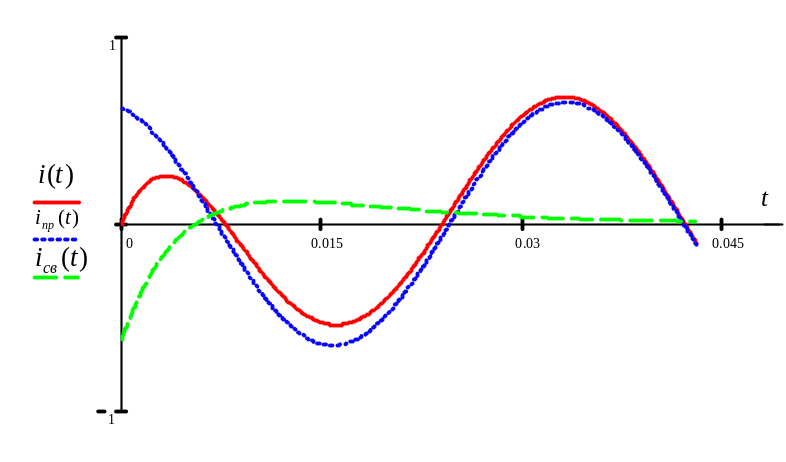
График тока построен при следующих параметрах цепи: 100 В, , 180 , 16 Ом, 0,2 Гн, =100 мкФ.( 220 > , ):

Частота установившегося тока равна частоте источника синусоидального напряжения , свободный ток изменяется с собственной частотой , которая в зависимости от параметров может быть больше или меньше .

Свободные колебания накладываются на установившийся ток и затухают . При совпадении и в цепи возникают биения.