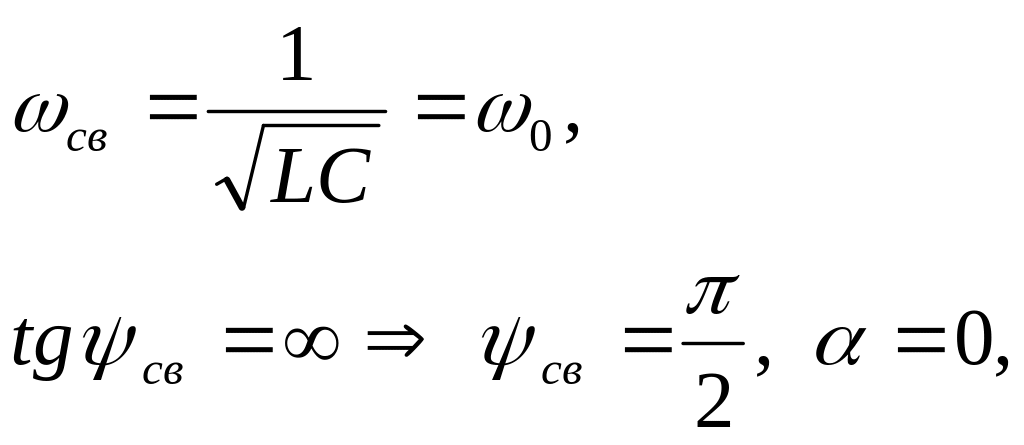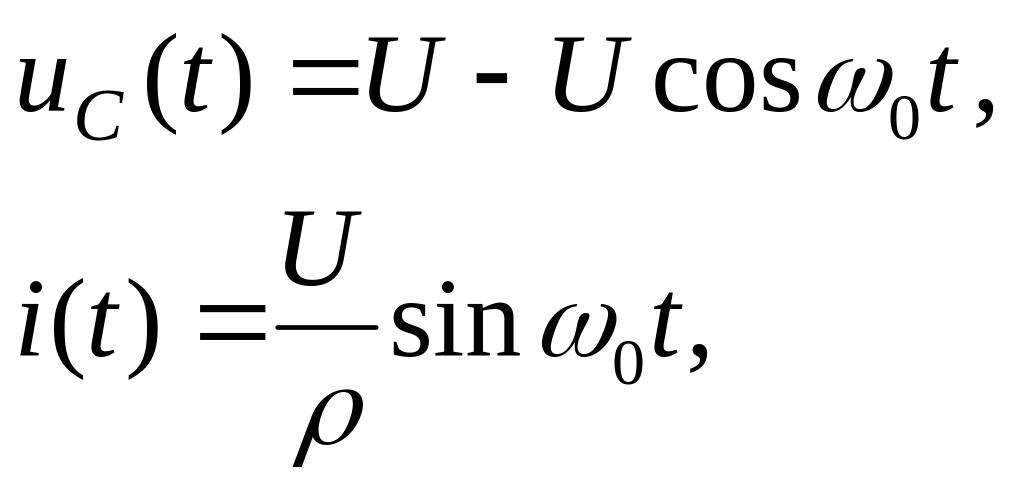6 П.П. В цепях второго порядка

По второму закону Кирхгофа т.к. , то

т.е. получаем неоднородное дифференциальное уравнение второго порядка.

Решение для напряжения на конденсаторе :

Дифференциальное уравнение относительно тока:

Решение для тока:

Принужденные составляющие, как и в цепях первого порядка, находятся из анализа послекоммутационной схемы для момента времени . Свободные составляющие определяются из решения однородных дифференциальных уравнений. Характеристическое уравнение имеет вид:

, или ,

где коэффициент затухания, , угловая частота затухающих колебаний.

При этом: .

Вид корней характеристического уравнения определяет решение однородного дифференциального уравнения, т.е. решение зависит от соотношения параметров элементов схемы.

Число корней характеристического уравнения равно степени уравнения:

1) –2 отрицательных неравных вещественных корня

Это апериодический п.п. и решение для свободных составляющих имеет вид

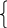
2) – два отрицательных вещественных равных корня: , .

Это критический случай протекания п.п. и решение для свободных составляющих имеет вид

3) –2 комплексно – сопряженных корня

или , .

Это колебательный п.п.

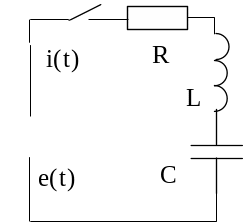
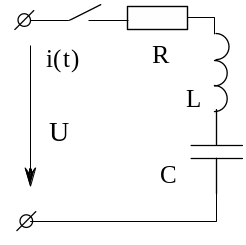
a) Включение R – L– C цепи на постоянное напряжения

Принужденная составляющая тока равно нулю, а принужденная составляющая напряжения на конденсаторе . 1) Апериодический процесс Т.к. постоянных интегрирования две для их определения требуется два уравнения.

Для получения второго уравнения найдем производную напряжения на конденсаторе:

Определяем постоянные интегрирования из начальных условий:

подставляя В₂

в первое уравнение, получим:

.

Решение для переходного напряжения на конденсаторе запишется следующим образом:

Для тока:

Для напряжения на катушке: .

При этом . Напряжение монотонно возрастает от нуля до напряжения источника питания, причем точка перегиба кривой при , определяется моментом, когда ток достигает максимального значения.

2) В случае кратных корней , .

Определяем постоянные интегрирования для момента времени :

Решение для напряжения на конденсаторе:

Для тока:

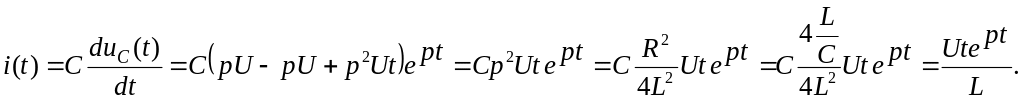
Для напряжения на индуктивности:

Переходной процесс при кратных корнях более близок к апериодическому процессу.

3) Колебательный п.п. Разрядка будет периодической, если сопротивление контура будет меньше критического, т.е. .

, так что .

Принужденный ток , а , тогда решение для :

Для тока:

При :

Откуда имеем , т.к. .

Решения запишем следующим образом:

,

.

Заменим выражение амплитудными значениями напряжений на индуктивности и емкости , а ток ,

и учитывая, что ,

где , получим более удобную запись для переходных тока и напряжений на индуктивности и емкости:

,

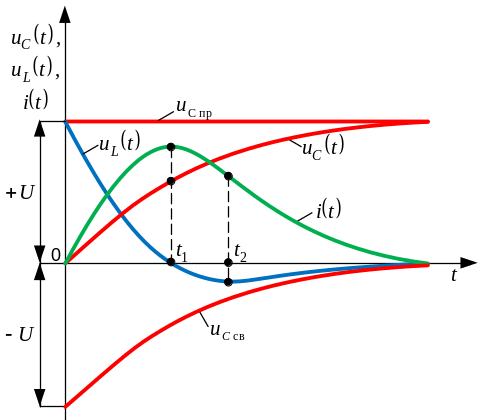
Ток совершает затухающие колебания относительно нулевого значения, а напряжение колеблется относительно установившегося значения. Заслуживает внимания случай, когда . (В идеале ). В этом случае т.е.

Ток и напряжение изменяются гармонически с частотой свободных колебаний, при этом колеблются в пределах .
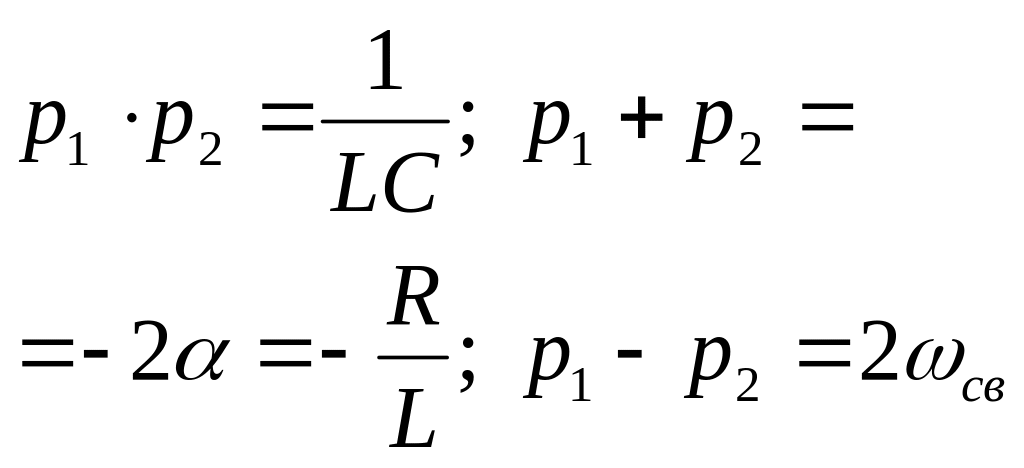