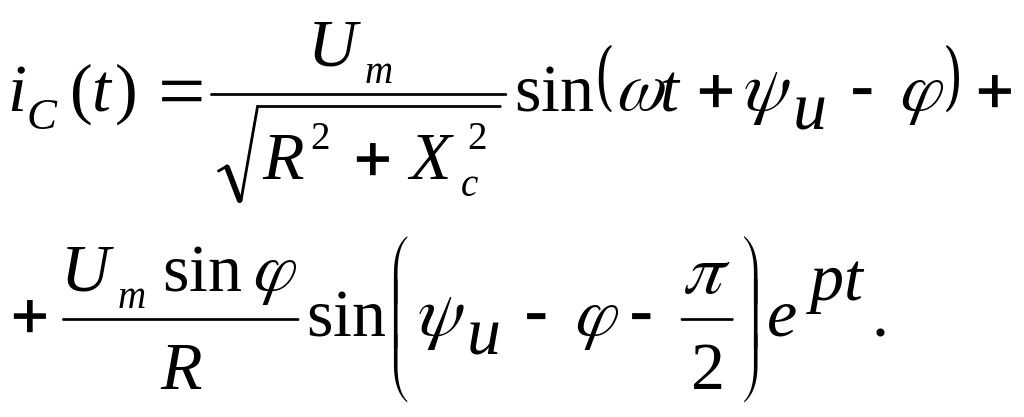- •Классический метод расчета переходных процессов в линейных электрических цепях
- •1 Возникновение переходных процессов и законы коммутации
- •2 Начальные значения величин
- •3 Математические основы анализа п.П. Принужденные и свободные составляющие токов и напряжений
- •4 Переходные процессы в r – l цепи а) Включение r – l цепи на постоянное напряжение
- •Б) Короткое замыкание r – l цепи
- •В) Включение r – l цепи на синусоидальное напряжение
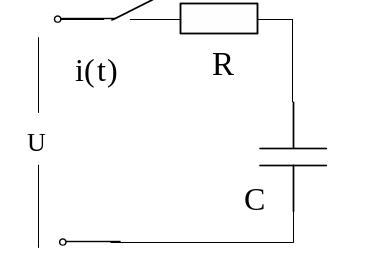
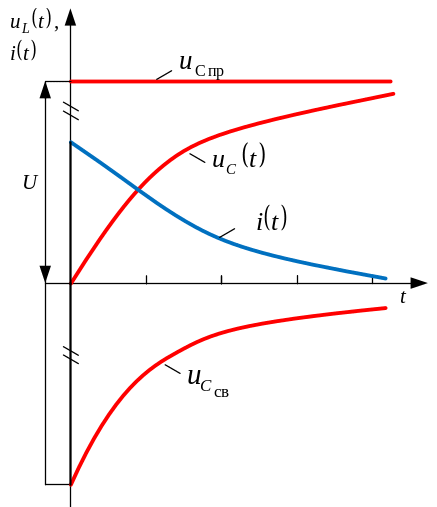
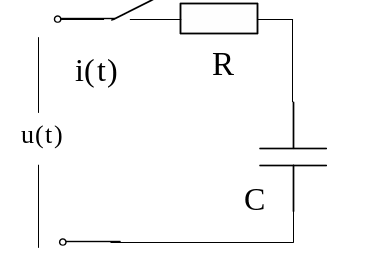
- •5 П.П. В r – c цепи а) Включение r – c цепи на постоянное напряжение
- •Б) Короткое замыкание r – c цепи
- •В) Включение r – c цепи на синусоидальное напряжение
- •6 П.П. В цепях второго порядка
- •Б) Разряд емкости на r – l цепь
- •В) Включение r – l– c цепи на синусоидальное напряжение
- •7 Переходные процессы в цепях с взаимной индуктивностью
- •7.11 Расчет переходных процессов в сложной цепи
- •Операторный метод расчета переходных процессов в линейных электрических цепях
- •1 Прямое преобразование Лапласа
- •2 Основные свойства преобразования Лапласа и изображение простейших функций
- •3 Некоторые теоремы и предельные соотношения
- •4 Законы электрических цепей в операторной форме
- •5 Эквивалентные операторные схемы
- •6 Расчет цепей операторным методом
- •7 Формулы соответствия
- •8 Нахождение оригинала по изображению с помощью обратного преобразования Лапласа
- •9 Дифференцирование и интегрирование электрическим путем. Интегрирующие и дифференцирующие цепи
- •10 Дельта-функция, единичная функция. Импульсная переходная проводимость
- •11 Переходная проводимость и переходная функция
- •1 2 Интеграл Дюамеля
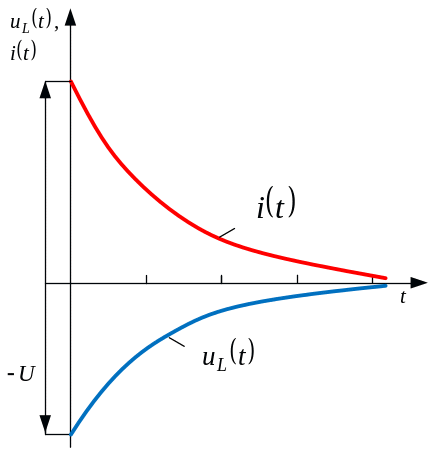
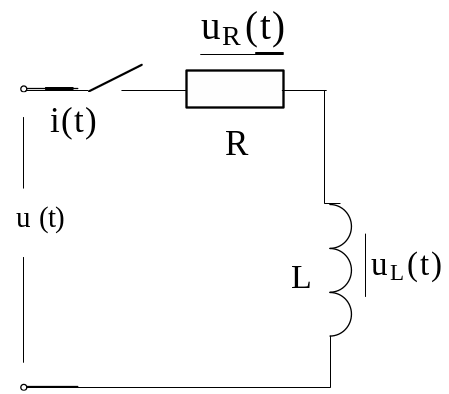
Б) Короткое замыкание r – l цепи
Ветвь с сопротивлением и индуктивностью (например, реальная катушка) замыкается мгновенно накоротко.
Ток в катушке до
коммутации был постоянным:
![]()
![]()
|
По первому закону
коммутации:
Установившийся
ток в катушке равен нулю. Следовательно,
переходной ток равен свободной
составляющей
|
|
|
|
Однородное дифференциальное для к.з. контура:
|
||
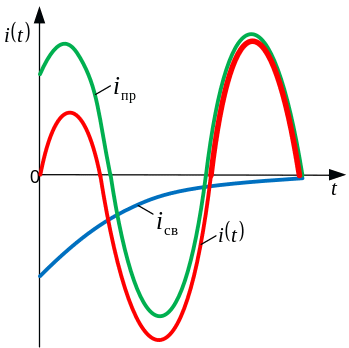
В) Включение r – l цепи на синусоидальное напряжение
|
При включении
где
|
![]()
В рассматриваемой
электрической цепи тока до коммутации
не было, поэтому при
![]()
![]()
![]()
Напряжение на индуктивности
![]()
(![]() ).
).
При
![]() для напряжения на индуктивности
для напряжения на индуктивности
![]() действительно в
момент
действительно в
момент
![]()
![]() (напряжению на источнике), т.к.
(напряжению на источнике), т.к.
![]() .
.
Наибольшего
возможно значения ток достигает, если
в момент включения цепи принужденная
составляющая
![]() равняется амплитудному значению, т.е.
если
равняется амплитудному значению, т.е.
если
![]() ,
а постоянная времени
велика (
,
а постоянная времени
велика (![]() ),
т.е.
),
т.е.
![]() затухает очень медленно.
затухает очень медленно.
|
|
5 П.П. В r – c цепи а) Включение r – c цепи на постоянное напряжение
По второму закону
Кирхгофу
![]() если учесть что,
если учесть что,
![]() то
получим дифференциальное уравнение
первого порядка:
то
получим дифференциальное уравнение
первого порядка:
![]() решение
уравнения
решение
уравнения
![]() .
.
![]() установившейся
режим.
установившейся
режим.
![]() решение
однородного дифференциального уравнения.
решение
однородного дифференциального уравнения.
|
Тогда
|
|
|
|
Ток в цепи с
конденсатором:
Величина
|
||
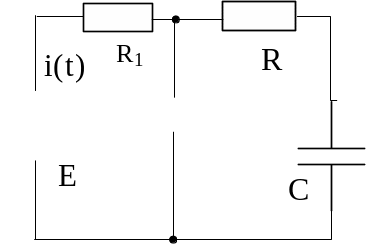
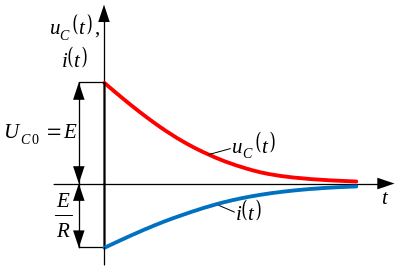
Б) Короткое замыкание r – c цепи
|
В этом случае могут быть два случая.
Предположим, что
на момент коммутации напряжение на
конденсаторе равнялось напряжению
источника питания
В соответствии со вторым законом Кирхгофа для к.з. контура
|
Решение для
напряжения будет состоять только из
свободной составляющей:
![]() где
где
![]() .
Постоянная интегрирования
.
Постоянная интегрирования
![]() из начальных
из начальных
|
условий равна:
|
В) Включение r – c цепи на синусоидальное напряжение
![]() В соответствии со
вторым законом Кирхгофа,
В соответствии со
вторым законом Кирхгофа,
![]() заменяя выражение
для тока
заменяя выражение
для тока
![]() ,
получим
,
получим
|
дифференциальное уравнение относительно напряжения на конденсаторе:
|
Принужденные составляющие тока и напряжения определяются из установившегося режима:
![]()
![]() ,
,
где
![]()
![]()
Переходное напряжение на конденсаторе будет описываться следующим образом:
![]()
Для определяем постоянную интегрирования В,
![]() ,
окончательно имеем:
,
окончательно имеем:
![]()
![]()
|
Ток через конденсатор в момент коммутации
|


 а)
а)