Классический метод расчета переходных процессов в линейных электрических цепях

1 Возникновение переходных процессов и законы коммутации

В электрических цепях могут происходить включения и отключения пассивных или активных элементов и ветвей, к.з. отдельных участков, различного рода переключения, внезапные изменения параметров и т.д. В результате таких изменений, называемых коммутационными (или просто коммутации) в цепи возникают переходные процессы, заканчивающиеся спустя некоторое время после коммутации (теоретически ). Т.е. переходным процессом (п.п.) называется процесс, протекающий в электрической цепи между двумя её устойчивыми состояниями.

Задача исследования и расчета переходного процесса заключается в том, чтобы установить:

1) по какому закону будет происходить изменение токов и напряжений на участке цепи от их установившихся значений;

2) как долго будут наблюдаться отклонения токов и напряжений от их установившихся значений (т.е. длительность п.п. )

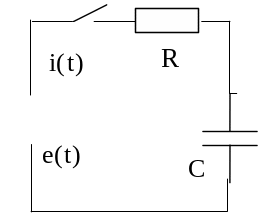
Физически п.п. представляют собой процессы перехода от энергетического состояния, соответствующего докоммутационному режиму, к энергетическому состоянию, соответствующего послекоммутационному режиму.

Во время п.п. токи в цепях и падения напряжений на участках электрической цепи определяются не только «внешними», но и «внутренними» источниками - накопителями энергии (индуктивностями и емкостями).

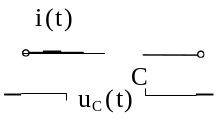
В момент коммутации, с которого начался отсчет времени п.п., начинается перераспределение энергии между внутренними накопителями (L и С), а также между L - С элементами и внешними источниками энергии.

При изменении энергии, накопленной в катушках индуктивности и конденсаторах нельзя допускать скачкообразных изменений мощности, т.к. потребовался бы источник бесконечной мощности.

Т.е. при любых п.п. соблюдают два основных положения:

Ток через индуктивность и напряжение на емкости не могут изменяться скачком.

Доказательство того, что ток через индуктивность не может измениться скачком, проведем на примере.

По второму закону Кирхгофа:

ток и ЭДС е(t) принимают конечные значения). Допустим, что ток i(t) может измениться скачком, Т.е. за бесконечно малый промежуток времени , ток изменится на конечную величину . При этом тогда , т.о., если в уравнении вместо подставить , не будет выполняться второй закон Кирхгофа.

Аналогично можно доказать и для напряжения на конденсаторе.

. Т.к. то Однако и могут изменяться скачком.

Из указанных двух основных положений следует два закона коммутации.

Первый закон. В индуктивном элементе ток (и магнитный поток) непосредственно после коммутации в момент, который и назван моментом коммутации, сохраняет значение, которое он имел непосредственно перед коммутацией и дальше начинает изменяться именно с этого значения.

коммутации.

Второй закон. На емкостном элементе напряжение (и заряд) сохраняет в момент коммутации то значение, которое оно имело непосредственно перед коммутацией, и в дальнейшем изменяется. Начиная с этого значения:

При анализе п.п. в линейных электрических цепях принимают следующие допущения:

1) Считают, что рубильники замыкаются и размыкаются мгновенно, без возникновения электрической дуги.

2) Время п.п., имеет условный предел, хотя теоретически п.п. продолжается бесконечно долго в силу асимптотического характера.

3) Установившийся режим будем рассчитывать при теоретическом условии, что п.п. уже полностью закончился.

4) Режим до коммутации будем рассчитывать из условия, что предыдущий п.п., тоже закончился.