2 Постановка задачи

Найти максимальный поток в графе (рисунок 2). Исток ­– вершина А. Сток – вершина В.

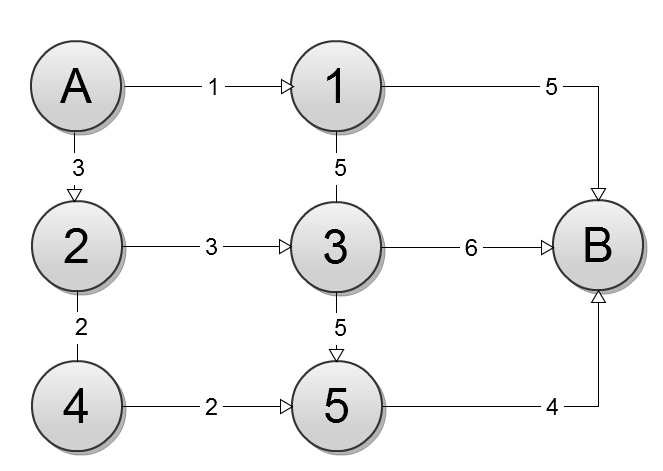
Рисунок 2 – Исходный граф

3 Решение задачи аналитическим методом

Алгоритм представляет собой несколько фаз. На каждой фазе (итерации) сначала строится остаточная сеть, затем по отношению к ней строится слоистая сеть (обходом в ширину), а в ней ищется произвольный блокирующий поток. Найденный блокирующий поток прибавляется к текущему потоку, и на этом очередная итерация заканчивается.

В первой итерации построим вспомогательную сеть (рисунок 3) такую, чтоб был достижим сток. Для этого сначала из истока обходим сеть в ширину и помечаем все вершины единицей, затем из каждой вершины обходом в ширину помечаем все последующие вершины двойкой и так, пока не достигнем стока.

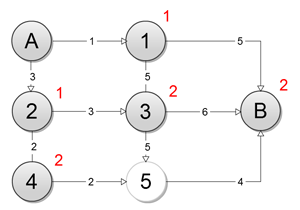
Рисунок 3 – Вспомогательная сеть

Построение вспомогательной сети завершено. Расстояние до стока в ней равно 2.

Перейдем к построению псевдо максимального потока во вспомогательной сети (рисунок 4). Псевдо максимальным или блокирующим потоком в некоторой сети, называется такой поток f, что любая цепь из истока в сток содержит дугу, полностью насыщенную потоком f. То есть этот поток нельзя увеличить, лишь изменив поток по некоторым дугам на больший.

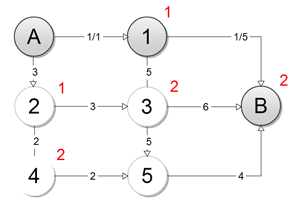
Рисунок 4 – Псевдо максимальный поток

Псевдо максимальный поток построен, его величина равна 1. Суммарный поток во всей сети равен 1. Заметим что дуга (A, 1) насыщенна, и в последующих итерациях пустить по ней поток мы уже не сможем.

Притупим ко второй итерации. Аналогично построим вспомогательную сеть, такую, что будет достижим сток (рисунок 5).

Рисунок 5 – Вспомогательная сеть

Вспомогательная сеть построена. Расстояние до стока равно 3. Перейдём к построению псевдо максимального потока (рисунок 6).

Рисунок 6 – Псевдо максимальный поток

Псевдо максимальный поток найден. Его величина равна 3. Суммарный поток в сети равен сумме всех псевдо максимальный потоков и равен 4. Заметим, что дуга (А, 2) насыщенна и исключается из сети.

В третьей итерации пытаемся построить вспомогательную сеть (рисунок 7).

Рисунок 7 – Вспомогательная сеть

Из истока выходят два ребра, но они оба насыщенны, значит, сток не достижим. На этом поиск максимального потока завершен. Максимальный поток в сети равен 4 (рисунок 8).

Рисунок 8 – Максимальный поток

4 Создание приложения для решения задачи

4.1 Описание алгоритма

Алгоритм программы представлен на рисунке 9.

S = исток

F = 0 //макс. поток

k = 0

Обход вершин из S в ширину и помечаем вершины k+1

Выделение пути из истока в сток

Максимальный поток = F

D = ребро с минимальной пропускной способностью

Увеличение потока по всем ребрам из истока в сток на величину D

F = F+D

Рисунок 9 – Блок схема

4.2 Разработка программы

Для разработки программы был выбран язык Delphi и среда разработки Borland Turbo Delphi 2006. Для ввода матрицы смежности реализован класс DrawGraph, который обеспечивает ввод, удаление, изменение и вывод вершин и ребер в окне программы, а так же генерирует матрицу смежности. Поиск максимального потока реализован методом Диница. Метод состоит из итераций, в начале каждой итерации производится обход вершин графа и их нумерация от истока к стоку, для этого реализована процедура TurboMark, принимающая один параметр - индекс источника в матрице смежности.

Функция TurboMark обходом в ширину нумерует каждую вершину графа. Истоку присваивается значение 0, вершинам смежным и стоком 1 и так далее.

После завершения работы процедуры TurboMark начинается цикл, в которым вызывается функция track.

Функция track, на основе пометок вершин графа, находит путь от стока к истоку и ребро с минимальной пропускной способностью (D) в этом пути, затем уменьшает пропускную способность ребер в этом пути на величину D и возвращает число D.

Цикл завершается если track возвращает 0.

Значения, возвращаемые функцией track, суммируются и составляют максимальный поток в графе.

Если в какой либо итерации сток будет не пронумерован (то есть его пометка равна -1) то выполнение алгоритма останавливается.