
- •4. Вычислить
- •4. Вычислить
- •4. Вычислить
- •1) (─ 4, ─ 1) 2) (─ 4, 1) 3) (4, ─ 1) 4) Нет экстремума
- •2. Пусть . Тогда частная производная функции z по переменной y равна
- •4. Вычислить
- •3. Вычислить
- •4. Вычислить
- •2. Пусть . Тогда частная производная функции z по переменной X равна
- •4. Вычислить
- •2. Пусть . Тогда частная производная функции z по переменной y равна
- •4. Вычислить
- •4. Вычислить
Вариант 1
1. Функция y
= 2x![]() − 9x
− 9x![]() − 24x
+ 61 достигает минимума в точке x
= …
− 24x
+ 61 достигает минимума в точке x
= …
1) − 1 2) 2 3) 3 4) 4
2. Пусть
![]() .
Тогда частная производная функции z
по переменной x
равна
.
Тогда частная производная функции z
по переменной x
равна
1) 0 2)
![]() 3)
3)
![]() 4)
4)
![]()
3. Множество
первообразных функции f(x)
= е![]() имеет вид…
имеет вид…
1) – 7 е
+
C
2)
![]() е
+ C
3) е
+ С 4) ─
е
+ С
е
+ C
3) е
+ С 4) ─
е
+ С
4. Вычислить
![]()
1) 0 2) 1 3) 2 4) 3
5. Объем тела,
образованный вращением вокруг оси OX
фигуры, ограниченной линиями
![]() ,
,
![]() равен
равен
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
Вариант 2
1. Абсцисса точки перегиба графика функции y = 2x + 9x − 24x – 56 равна…
1) −2,5 2) 2,5 3) −1,5 4) 1,5
2. Пусть . Тогда частная производная функции z по переменной y равна
1) 0 2)
3)
![]() 4)
4)
3. Множество первообразных функции f(x) = cos(3 – 7x) имеет вид…
1) ─ cos x + C 2) ─ sin x + C 3) 7cos (3 – 7x) + C 4) ─ sin(3 – 7x) + С
4. Вычислить
![]()
1) 2![]() 2) 3
3) 4
4) 5
2) 3
3) 4
4) 5
5. Определить
площадь фигуры, ограниченной кривыми
![]() и
и
![]() .
.
1) 4/3 2) 2/3 3) 5/3 4) 1/3
Вариант 3
1. Функция y = 2x + 9x − 24x − 56 достигает максимума в точке x = …
1) − 5 2) − 4 3) − 3 4) 1
2. Пусть
![]() .
Тогда частная производная функции z
по переменной x
равна
.
Тогда частная производная функции z
по переменной x
равна
1)![]() 2)
2)![]() 3)
3)![]() 4)
4)
![]()
3. Множество первообразных функции f(x) = sin (5x + 5) имеет вид…
1) 5 cos(5x
+ 5) + C 2) – cos(5x + 5) + C 3) ─ 5 cos(5x + 5) + C
4) ─
![]() cos(5x + 5) + С
cos(5x + 5) + С
4. Вычислить
1) 1
2) 1 −
![]() 3)
4) 1 +
3)
4) 1 +
5. Найти длину
дуги кривой
![]() от точки x
= 0 до точки x
= 8
от точки x
= 0 до точки x
= 8
1) 54/3 2) 52/3 3) 55/3 4) 61/3
Вариант 4
1. Абсцисса точки перегиба графика функции y = 2x + 15x + 36x + 32 равна…
1) 1,5 2) − 2,5 3) 0 4) − 1,5
2. Пусть . Тогда частная производная функции z по переменной y равна
1)
2)
3)![]() 4)
4)
![]()
3. Множество
первообразных функции f(x)
=
![]() имеет вид…
имеет вид…
1) ─ 6
+ C
2)
![]() + C
3)
+ C
4) 6
+ C
+ C
3)
+ C
4) 6
+ C
4. Вычислить
1) 0 2) 1 3) 1 + 4)
5. Вычислить
![]()
1) 2ln
![]() + C
2) ln
+ C
3) ln
+ C
2) ln
+ C
3) ln
![]() + C
4) 3ln
+ C
+ C
4) 3ln
+ C
Вариант 5
1. Функция y = 2x + 15x + 36x + 32 достигает максимума в точке x = …
1) 0 2) − 3 3) 3 4) − 2
2. Пусть
![]() .
Тогда частная производная функции z
по переменной x
равна
.
Тогда частная производная функции z
по переменной x
равна
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
3. Множество
первообразных функции f(x)
= 3![]() имеет вид…
имеет вид…
1)
![]() 3
+ C
2) 3
+ C
3) ─ 3
6ln3
+ C
4) ─ 3
+ С
3
+ C
2) 3
+ C
3) ─ 3
6ln3
+ C
4) ─ 3
+ С
4. Вычислить
1) 3ln3 – 2ln2 – 1 2) ln3 – 2ln2 – 1 3) 3ln3 – ln2 – 1 4) 3ln3 + ln2 – 1
5. Функция
![]() имеет экстремум в точке
имеет экстремум в точке
1) (─ 4, ─ 1) 2) (─ 4, 1) 3) (4, ─ 1) 4) Нет экстремума
Вариант 6
1. Абсцисса точки перегиба графика функции y = 2x − 15x + 24x + 4 равна…
1) 2,5 2) 0,4 3) − 2,5 4) − 0,4
2. Пусть . Тогда частная производная функции z по переменной y равна
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
3. Множество
первообразных функции f(x)
=
![]() имеет вид…
имеет вид…
1)
![]() ln
(8x + 5) + C 2) ln x + C 3) 8ln (8x + 5) + C
4)
ln
x + С
ln
(8x + 5) + C 2) ln x + C 3) 8ln (8x + 5) + C
4)
ln
x + С
4. Вычислить
1) 1 2) 0 3) 2 4) 3
5. Вычислить площадь
фигуры, ограниченной линиями, уравнения
которых
![]() и
и
![]()
1) 4/3 2) 5/3 3) 8/3 4) 16/3
Вариант 7
1. Наклонная
асимтота графика функции y
=
![]() есть…
есть…
1) y = x – 1 2) y = x +1 3) y = x 4) y = x + 2
2. Пусть
![]() .
Тогда частная производная функции z
по переменной x
равна
.
Тогда частная производная функции z
по переменной x
равна
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
3. Вычислить
1) ln
│![]() ─ 5│+ C
2) 2 ln
│
─ 5│+ C
3) ─ ln
│
- 5│+ C
4) 0,5 ln
│
─
5│+ C
─ 5│+ C
2) 2 ln
│
─ 5│+ C
3) ─ ln
│
- 5│+ C
4) 0,5 ln
│
─
5│+ C
4. Вычислить
1)
2) ─
3)
![]() 4) ─
4) ─
5. Определить
площадь фигуры, ограниченной кривыми
![]() ,
x
= ─ 2, x
= 2.
,
x
= ─ 2, x
= 2.
1) 0 2) 2 3) 8 4) 4
Вариант 8
1. Наклонная
асимтота графика функции y
=
![]() есть…
есть…
1) y = x – 2 2) y = x 3) y = 1 4) y = − x
2. Пусть . Тогда частная производная функции z по переменной y равна
1) 2) 3) 4)
3. Вычислить
![]()
1) 2ln(1
+ x
)
+ C
2)
![]() + C
3) ln
x
+ C
4) ln(1
+ x
)
+ C
+ C
3) ln
x
+ C
4) ln(1
+ x
)
+ C
4. Вычислить
![]()
1)
![]() 2)
+
2)
+
![]() 3)
3)
![]() +
4)
+ 5
+
4)
+ 5
5. Вычислить
![]()
1) ln
![]() + C
2) ln
+ C
2) ln
![]() + C
3) ln
+ C
3) ln
![]() + C
4) ln
+ C
4) ln
![]() + C
+ C
Вариант 9
1. Какой эскиз соответствует поведению функции y(x) в окрестности точки М, если
y`(M) < 0; y``(M) < 0 ?
1)
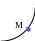 2)
2)
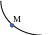 3)
3)
 4)
4)

2. Пусть
![]() .
Тогда частная производная функции z
по переменной x
равна
.
Тогда частная производная функции z
по переменной x
равна
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
3. Множество первообразных функции f(x) = ctg x имеет вид…
1) tg x + C 2) ─ ln (cos x) + C 3) ctg x + C 4) ln (sin x) + С
4.
Вычислить
![]()
1) e
2) e![]() 3) ─ e
4) ─ e
3) ─ e
4) ─ e
5.
Вычислить
![]()
1) ln
![]() + C 2) ─ ln
+ C 2) ─ ln
![]() + C 3) ln
+ C 3) ln
![]() + C 4) ln
+ C
+ C 4) ln
+ C
Вариант 10
1. Функция y = x − 6x + 9x + 5 достигает максимума в точке x = …
1) − 2 2) 2 3) − 1 4) 1
2. Пусть . Тогда частная производная функции z по переменной y равна
1)
![]() 2)
2)
![]() 3)
4)
3)
4)
3. Множество
первообразных функции f(x)
=
![]() имеет вид…
имеет вид…
1) ─![]() ln
(1─7x)
+ C
2) 4ln(1─7x)
+ C
3) ln(1─7x)
+ C
4) ─
ln
(1─7x)
+ C
2) 4ln(1─7x)
+ C
3) ln(1─7x)
+ C
4) ─
![]() ln(1─7x)+
C
ln(1─7x)+
C
4. Вычислить
![]()
1) 0 2) 1 3) 2 4) 3
5. Вычислить
![]()
1)![]() 2)
2)![]()
3)![]() 4)
4)![]()
Вариант 11
1. Функция y
=
![]() − 2x
+ 3x
− 1 достигает максимума в точке x
= …
− 2x
+ 3x
− 1 достигает максимума в точке x
= …
1) − 2 2) 2 3) − 1 4) 1
2. Пусть
![]() .
Тогда частная производная функции z
по переменной x
равна
.
Тогда частная производная функции z
по переменной x
равна
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
3. Множество
первообразных функции f(x)
=
![]() имеет вид…
имеет вид…
1)
![]() + C
2)
+ C
2)
![]() + C
3)
+ C
3)
![]() + C
4)
+ C
4)
![]() +
C
+
C
4. Вычислить
![]()
1) 0 2) 1 3) 2 4) 3
5. Функция
![]() (x
> 0, y
> 0) имеет экстремум в точке
(x
> 0, y
> 0) имеет экстремум в точке
1) (3, ─ 2) 2) (─ 3, 2) 3) нет экстремума 4) (3, ─ 2)
Вариант 12
1. Какой эскиз соответствует поведению функции y(x) в окрестности точки М, если
y`(M) < 0; y``(M) > 0 ?
1)
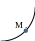 2)
2)
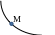 3)
3)
 4)
4)
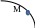
2. Пусть . Тогда частная производная функции z по переменной y равна
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
3. Множество
первообразных функции f(x)
=
![]() имеет вид…
имеет вид…
1)
![]() + C
2)
+ C
2)
![]() +
C
3)
+
C
3)
![]() +
C
4)
+
C
4)
![]() +
C
+
C
4. Вычислить
![]()
1) 1 2) 2 3) 3 4) 4
5. Вычислить площадь
фигуры, ограниченной линиями, уравнения
которых
![]() ,
,
x = 2, x = 8
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
Вариант 13
5. Функция y
=
![]() достигает максимума в точке x
= …
достигает максимума в точке x
= …
1) 1 2) 2 3) 3 4) 4
