24. Ошибки измерений. Равноточные и неравноточные измерения.

Когда многократные измерения какой либо величины производит один наблюдатель, одним и тем же инструментом, методом и при одинаковых условиях окруж среды то такие измерения называют равноточными. Если измерения произведены в различных условиях различными наблюдателями и методом, то их называют неравноточные

Ошибки результатов измерения:

Грубые; систематические; случайные; постоянные; переменные; элементарные ошибки( объекта, субъекта, прибора, метода, среды)

Грубые – ошибки превосходят по абсолютным величинам некоторых установленных при данных условиях изменения предела, они получаются при невнимательных исполнениях для выявления грубых ошибок, происходит в не бытное измерение, грубые ошибки проходят и изменяют новыми.

Систематические – это ошибки которые при многократной изменение либо остаются без изменения либо изменяются по опред. Законную

Постоянные – результаты входят в каждый результат измерения незменными как по закону так и по величине.

Переменные – изменяет свою величину от изменения к другому по определенному закону.

Систематические ошибки должны быть изучены и исключены путем введения соотв. Поправок.

Случайные – возникновение их не удается подчинить определению аналитическим закономерностям, они подчиняются закономерностям массовыми случайными явлениями.

25. Сущность геодезических разбивочных работ

Разбивочные работы представляют собой один из наиболее частых видов инженерно-геодезических изысканий. Они выполняются с целью определить на местности высотное и плановое положение характерных плоскостей и точек возводимого сооружения. Проект сооружения составляют при этом на крупномасштабных топографических планах.

Разбивочные работы подразумевают определение расположения проектируемого здания относительно сторон света и окружающих его объектов. Помимо этого, топографический план призван определить систему координат, которая задает расположение характерных точек проектируемой конструкции относительно данной системы. Вынесение проекта в натуру является работой по нахождению на местности точек конструкции по указанным в проекте координатам.

Разбивочные геодезические работы являются взаимосвязанным комплексным процессом, который представляет собой неотъемлемую часть монтажно-строительного производства. По этой причине технология и организация разбивочных работ напрямую зависят от строительных этапов. Компоновку сооружения определяют геометрией конструкции, которую задают осями. В рабочих чертежах указывается местоположение каждого элемента относительно осей.

Данные работы, в особенности когда речь идет о детальной разбивке, очень сложны. Их необходимо доверять исключительно профессионалам. Только опытный специалист сможет максимально точно определить и обозначить все координаты. Без разбивочных геодезических работ постройка здания или любого другого объекта невозможна, а некачественное выполнение их может привести к печальным последствиям.

26. Построение проектного горизонтального угла

В горизонтальной плоскости проектный (расчетный) угол Р можно построить двумя способами.

Способ первый. Теодолит устанавливают в точке В исходного направления (АВ), визируют на точку А и берут отсчет а по горизонтальному кругу. Вычисляют отсчет с = а р. Устанавливают отсчет с на горизонтальном круге и по сетке нитей трубы фиксируют точку С1. Аналогично строят угол р при другом положении вертикального круга и фиксируют точку С2. Отрезок С1С2 делят пополам и фиксируют точку С, полученный < АВС принимают за проектный (рис. 15). Предельная погрешность < АВС при таком построении близка к удвоенной точности отсчетного приспособления теодолита, т. е. ∆β ≈ ±2t. Для контроля < АВС измеряют и сличают с проектным.

Способ второй (точный). В точке В при одном положении вертикального круга откладывают проектный угол и фиксируют точку С3. Предварительно отложенный угол < АВС3 измеряют с погрешностью, вдвое меньшей расчетной погрешности построения проектного угла (рис. 16).

По разнице β — βи находят поправку ε, на которую необходимо исправить предварительно отложенный угол.

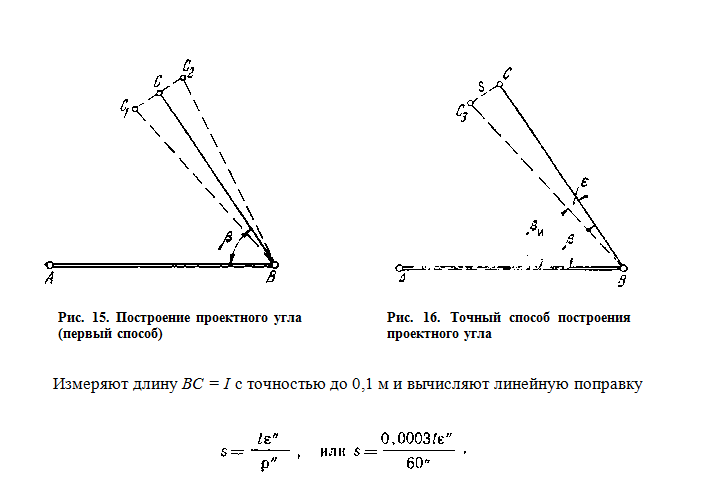
Последней формулой часто пользуются на практике. Здесь 0,0003 — значение тангенса угла, равного одной минуте (tg 1 = 0,0003).

От точки С3 рулеткой откладывают s и фиксируют точку С. Угол ∆АВС будет соответствовать проектному в границах заданной погрешности.

Погрешности построения горизонтального угла. Наибольшее влияние на точность построения угла оказывают инструментальные погрешности, погрешности центрирования теодолита и сигналов. Линейная величина погрешности центрирования sц в зависимости от вида центрировочного приспособления, его юстировки, высоты теодолита над вершиной угла. Линейная погрешность фиксации угла яф в зависимости от способа закрепления точки на различных поверхностях.

В практике для определения необходимой точности построения угла исходят из предельной погрешности АС положения точки С. Абсолютную линейную величину этой погрешности принимают равной 3—5 м в зависимости от типа и назначения сооружения. Определение положения точки С полярным способом производят при единичных измерениях угла, когда свойства случайных погрешностей могут не проявляться вовсе, поэтому все расчеты делают по предельным погрешностям.

Предварительный расчет точности построения угла по всем источ¬никам погрешностей сложен и на практике применяется только для высокоточных (прецизионных) работ.

Для того чтобы не завышать точность геодезических измерений при разбивочных работах и в то же время учитывать влияние основных погрешностей на положение точки С, при расчетах применяют принцип пропорционального изменения погрешностей. Коэффициент пропорциональности принимают равным двум.

Расчет погрешности построения угла Р выполняют следующим образом.

Определяют линейную погрешность δβ положения точки С, зависящую от погрешности построения угла 0:

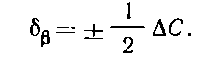
Затем определяют допустимую погрешность построения угла без учета погрешности центрирования инструмента