5Геодезическая задача

Геодезическая задача – математического вида задача, связаная с определением взаимного положения точек земной поверхности и подразделяется на прямую и обратную задачу.

П рямой геодезической задачей (ПГЗ) называют вычисление геодезических координат - широты и долготы некоторой точки, лежащей на земном эллипсоиде, по координатам другой точки и по известным длине идирекционному углу данного направления, соединяющей эти точки.

Обратная геодезическая задача (ОГЗ) заключается в определении по геодезическим координатам двух точек на земном эллипсоиде длины и дирекционного угла направления между этими точками.

В зависимости от длины геодезической линии, соединяющей рассматриваемые точки, применяются различные методы и формулы, разработанные в геодезии. По размерам принятого земного эллипсоида (см. Эллипсоид Красовского) составляются таблицы, облегчающие решение геодезических задач и рассчитанные на использование определённой системы формул.

В обратной геодезической задаче находят дирекционный угол и расстояние:

1) Вычисляют румб по формуле:

2) Находят дирекционный угол в зависимости от четверти угла:

четверти:	Первая четверть	Вторая четверть	Третья четверть	Четвертая четверть
знак приращения	+X, +Y	-X, +Y	-X, -Y	+X, -Y
диреционный угол	a = r	a = 180 - r	a = 180 + r	a = 360 - r

3) Определяют расстояние между точками:

  

Геодезическая задача в том и другом виде возникает при обработке полигонометрии и триангуляции, а также во всех тех случаях, когда необходимо определить взаимное положение двух точек по длине и направлению соединяющей их линии или же расстояние и направление между этими точками по их геодезическим координатам. В ряде случаев геодезические задачи решают в пространственных прямоугольных координатах по формулам аналитической геометрии в пространстве. В этих случаях вместо длины и дирекционного угла, соединяющей две точки, используют длину и пространственные компоненты направления прямой линии между этими точками.

 

6Способы съемки ситуации

Съемка ситуации – геодезические измерения на местности для последующего нанесения на план ситуации (контуров и предметов местности).

Выбор способа съемки зависит от характера и вида снимаемого объекта, рельефа местности и масштаба, в котором должен быть составлен план .

Съемку ситуации производят следующими способами: перпендикуляров; полярным; угловых засечек; линейных засечек; створов (рис. 60).

 Способы съемки ситуации:

1) способ перпендикуляров;

2) полярный способ;

3) способ угловых засечек;

4) способ линейных засечек;

5) способ створов.

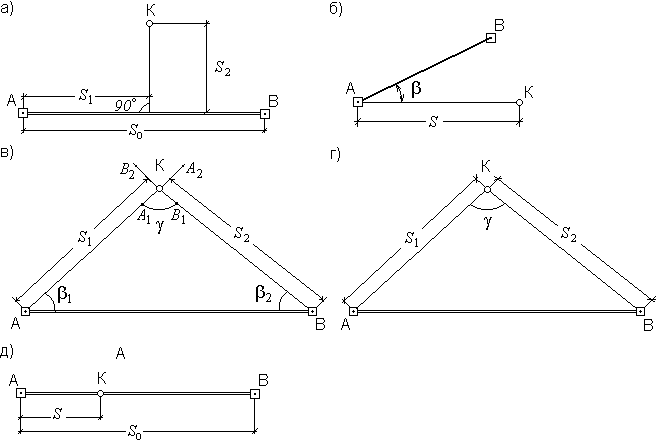
Рис. 60. Способы съемки ситуации:

 а – перпендикуляров, б – полярный, в – угловых засечек, г – линейных засечек, д – створов.

Способ перпендикуляров (способ прямоугольных координат) – применяется обычно при съемке вытянутых в длину контуров, расположенных вдоль и вблизи линий теодолитного хода, проложенных по границе снимаемого участка. Из характерной точки К (рис. 60, а) опускают на линию хода А – В перпендикуляр, длину которого S₂ измеряют рулеткой. Расстояние S₁ от начала линии хода до основания перпендикуляра отсчитывают по ленте.

Полярный способ (способ полярных координат) – состоит в том, что одну из станций теодолитного хода (рис.60, б) принимают за полюс, например, станцию А, а положение точки К определяют расстоянием S от полюса до данной точки и полярным углом β между направлением на точку и линией А – В. Полярный угол измеряют теодолитом, а расстояние дальномером. Для упрощения получения углов, теодолит ориентируют по стороне хода.

 При способе засечек (биполярных координат) положение точек местности определяют относительно пунктов съемочного обоснования путем измерения углов β₁ и β₂ (рис.60, в) – угловая засечка, или расстояний S₁ и S₂ (рис.60, г) – линейная засечка.

Угловую засечку применяют для съемки удаленных или труднодоступных объектов.

Линейную засечку – для съемки объектов, расположенных вблизи пунктов съемочного обоснования. При этом необходимо чтобы угол γ, который получают между направлениями при засечке был не менее 30° и не более 150°.

Способ створов (промеров). Этим способом определяют плановое положение точек лентой или рулеткой.(рис. 60, д). Способ створов применяется при съемке точек, расположенных в створе опорных линий, либо в створе линий, опирающихся на стороны теодолитного хода. Способ применяется при видимости крайних точек линии. Результат съемки контуров заносят вабрис. Абрис называют схематический чертеж, который  составляется четко и аккуратно.

7методы нивелирования

Нивелирование – определение высот точек земной поверхности относительно исходной точки («нуля высот») или над уровнем моря.

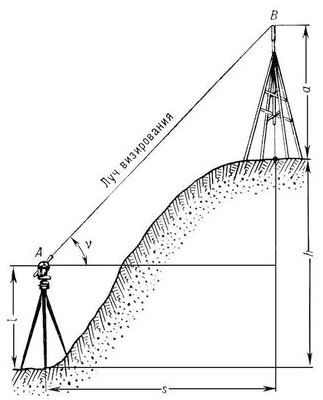
Нивелирование – один из видов геодезических измерений, которые производятся для создания высотнойопорной геодезической сети (т. е. нивелирной сети) и при топографической съёмке (см. топография), а также в целях проектирования, строительства и эксплуатации инженерных сооружений, железных и шоссейных дорог и т.д. Результаты нивелирования используются в научных исследованиях по изучению фигуры Земли, колебаний уровней морей и океанов, вертикальных движений земной коры и т.п.

По точности выполнения нивелирование делят на I, II, III, IV классы точности. I и II классы относят к высокоточному нивелированию, III и IV классы – к точному. Также в строительных работах применют менее точное – техническое нивелирование, которые ниже точности IV класса. Для каждого класса точности существует определенная методика выполнения работ.

По методу выполнения нивелирование различают: геометрическое, тригонометрическое, барометрическое, механическое игидростатическое нивелирование. При изучении фигуры Земли высоты точек земной поверхности определяют не над уровнем моря, а относительно поверхности референц-эллипсоида и применяют методы астрономического или астрономо-гравиметрического нивелирования.

Нивелирование возникло в глубокой древности в связи со строительством оросительных каналов, водопроводов и т.п. Первые сведения о водяном нивелире связывают с именами римского архитектора Марка Витрувия (1 в. до н. э.) и древнегреческого учёного Герона Александрийского (1 в. н. э.). Дальнейшее развитие методов нивелирования связано с изобретением зрительной трубы (конец 16 в.), барометра – Э. Торричелли (1648 г.), сетки нитей в зрительных трубах – Ж. Пикаром (1669 г.), цилиндрического уровня – английским оптиком Дж. Рамсденом (1768 г.).

8 способы геометрического нивелирования

 Способы геометрического нивелирования.

Геометрическое нивелирование выполняется горизонтальным лучом визирования. Перед нивелированием точки на местности закрепляют колышками, костылями,  башмаками,  на которые устанавливают вертикально нивелирные рейки. Место установки нивелира для работы называют станцией, а расстояние от нивелира до рейки - плечом нивелирования.

Различают два способа геометрического нивелирования: из середины и вперед. При нивелировании из середины (рис.30а) нивелир устанавливается примерно на равных расстояниях от реек,  поставленных на точки А  и В, а превышение вычисляют по формуле:

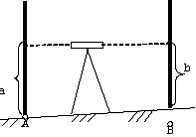
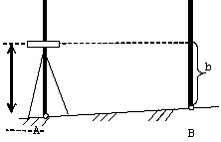
Рис.30. Способы геометрического нивелирования:

а - из середины;  б – вперед

h = a - b,

где а  и b - отсчеты в мм по рейкам,  установленным соответственно на задней по ходу движения при нивелировании и передней точках.

Знак превышения h получится положительным,  если а больше b, и отрицательным, если а меньше b. Если известна высота НА задней точки А, то высота передней точки В

НВ = НА + h.

При нивелировании вперед нивелир ставят так,  чтобы его окуляр находился над точкой А, измеряют высоту прибора i, затем визируя на рейку, отвесно поставленную в точке В, берут отсчет b. В этом случае:

h = i - b.

При нивелировании нескольких точек для вычисления их высот используют горизонт прибора,  которым называют высоту  горизонтальной  линии визирования, т.е.  горизонт прибора равен высоте точки, на которой установлена рейка, плюс отсчет по рейке. Из рис. 30 б следует:

ГП = HA + i;  НB = ГП - b.

Последовательное нивелирование применяется для измерения  превышений  между  точками  А и D,  разделенными значительным расстоянием или превышениями.