Аппроксимация

Пусть задана область G переменных x = (x₁,x₂,…,x_p) с границей  и поставлена корректная задача решения уравнения с граничными условиями:

Au(x)  f(x) = 0, x  G; (51)

Ru(x)  (x) = 0, x  . (52)

Введем в области G +  сетку с шагом h, которая содержит регулярные (внутренние) узлы _h и нерегулярные (граничные) узлы _h.

Перейдем в (51), (52) к соответствующим разностным аналогам

A_hy_h(x)  _h(x) = 0, x  _h; (51)

R_hy_h(x)  _h(x) = 0, x  _h. (52)

Близость разностной схемы (51), (52) к исходной задаче (51), (52) определяется величинами невязок:

;

.

Разностная схема (51), (52) аппроксимирует задачу (51), (52), когда

,

аппроксимация имеет p-й порядок, когда

.

Дадим некоторые комментарии к выбору норм. Для простоты будем рассматривать одномерный случай, т.е. G = [a,b].

Можно использовать чебышевскую или локальную норму

,

или гильбертову, среднеквадратическую:

.

Часто строят ассоциированные или связанные с оператором A энергетические нормы. Например,

.

Выбор нормы регулируется двумя противоположными соображениями. С одной стороны, желательно, чтобы разностное решение y было близко к точному решению в наиболее сильной^ норме. Например, в задачах на разрушение конструкций малость деформаций в не гарантирует целостность конструкций, а малость в норме — гарантирует. С другой стороны, чем слабее норма , тем легче разностную схему построить и доказать ее сходимость.

Функции y_h, _h, _h, входящие в (51), (52), определены на сетке, поэтому для них необходимо определить соответствующие сеточные нормы , и . Обычно их вводят так, чтобы они переходили в выбранные нормы , и при h  0. В качестве разностных аналогов чебышевской и гильбертовых норм выбирают выражения

или близкие аналоги.

Устойчивость

Под устойчивостью (неустойчивостью) разностной схемы понимается то, что малые ошибки, возникающие в процессе счета (или внесенные с входными данными), при последующих расчетах уменьшаются (возрастают).

Рассмотрим пример неустойчивой разностной схемы для задачи Коши дифференциального уравнения u =  u. Выберем следующее однопараметрическое семейство разностных схем:

. (53)

Исследуем рост ошибки y_n начальных данных уравнения (53). Поскольку уравнение (53) линейно, постольку ошибка y_n удовлетворяет тому же уравнению (53). Изучим специальный вид ошибки y_n = ⁿ. Подставим это представление в (53), тогда

. (54)

Решение квадратного уравнения (54) при h  0 дает следующие оценки корней

. (55)

Из оценок корней в (55) следует, что при  < ½ второй корень |₂| > 1, т.е. за один шаг ошибка возрастает в несколько раз. Проверим это.

На листинге_№5 приведен код программы, иллюстрирующей расчет по неустойчивой при  = 0,25 схеме (53) и по устойчивой схеме при  = 0,75. В начальных данных выбирались малые возмущения. Далее проводились серии расчетов с уменьшающимся значением шага сетки h. На рис.11 приведены итоговые графики зависимости значения возмущения в начальных данных на правом конце отрезка интегрирования в зависимости от шага сетки. Отчетливо видно сколь разительно отличаются друг от друга расчеты по неустойчивой и устойчивой схемам. Используя данную программу можно убедиться в пороговом значении параметра  = 0,5: при  < 0,5 схема неустойчива, при   0,5 — устойчива.

Листинг_№5

%Программа расчета по неустойчивой схеме при

%sigma=0,25 и по устойчивой схеме при sigma=0,75

%очищаем рабочее пространство

clear all

%определяем константу уравнения u'=alpha*u

alpha=1;

%определяем значения sigma=0,25; 0,75

sigm=0.25:0.5:0.75;

for s=1:length(sigm)

sigma=sigm(s);

%определяем начальное значение шага сетки

h=0.5;

for i=1:8

h=h/2;

x=0:h:1; N=length(x);

%определяем возмущения начальных данных

dy(1)=1e-6; dy(2)=1e-6;

%осуществляем расчет возмущения начальных

%данных на правом конце отрезка интегрирования

for n=2:(N-1)

dy(n+1)=(2+(alpha*h-1)/sigma)*dy(n)+...

(1/sigma-1)*dy(n-1);

end

%запоминаем возмущение на правом конце и

%шаг сетки

deltay(i)=dy(N);

step(i)=h;

end

%рисуем график зависимости возмущения на

%правой границе от шага сетки

plot(step,deltay);

hold on

end

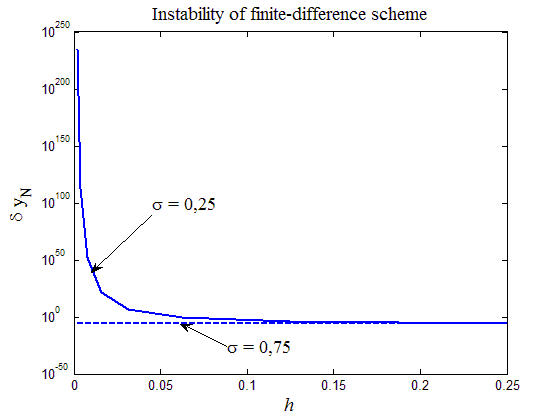
Рис.11. Графики зависимости возмущения при расчете по схеме (53) на правой границе от шага сетки h

Разностная схема (51), (52) устойчива⁴, если решение системы разностных уравнений непрерывно зависит от входных данных ,  и эта зависимость равномерна относительно шага сетки. Уточним непрерывную зависимость. Это означает, что для любого  > 0 найдется такое (), не зависящее от h, что

, (56)

когда

. (57)

Если разностная схема (51), (52) линейна, то разностное решение линейно зависит от входных данных. В этом случае можно положить, что () =  /(M + M₁), где M, M₁ — некоторые неотрицательные величины, независящие от h. В итоге условие устойчивости для линейных разностных схем можно записать в виде:

. (58)

Непрерывную зависимость разностного решения от  называют устойчивостью по правой части, а от  — устойчивостью по граничным данным.

В дальнейшем будем рассматривать двуслойные разностные схемы, т.е. такие схемы которые содержат один известный и один новый, неизвестный слой.

Двуслойная разностная схема называется равномерно устойчивой по начальным данным, если при выборе начальных данных с любого слоя t_* (t₀  t_* < T) разностная схема устойчива по ним, причем устойчивость равномерна по t_*. Для линейных схем условие равномерной устойчивости можно записать в виде

, (59)

где константа K не зависит от t_* и h, — решения разностной схемы A_hy =  с начальными данными и с одной и той же правой частью.

Достаточный признак равномерной устойчивости. Для равномерной устойчивости по начальным данным достаточно, чтобы при всех m выполнялось

. (60)

Доказательство. Условие (60) означает, что если на некотором слое возникла ошибка y, то при переходе на следующий слой норма возмущения ||y|| возрастает не более чем в (1 + С)  e^C раз. Согласно (59), при переходе со слоя t_* на слой t требуется m = (t  t_*)/ шагов по времени, т.е. ошибка возрастает не более чем в . В итоге имеем

,

что, согласно определению в (59), означает равномерную устойчивость по начальным данным.

Теорема. Пусть двухслойная разностная схема A_hy =  равномерно устойчива по начальным данным и такова, что если два разностных решения A_hy^k = ^k равны на некотором слое, т.е. , то на следующем слое выполняется соотношение

, (61)

где  = const. Тогда разностная схема устойчива по правой части.

Доказательство. Помимо решения y рассмотрим решение , соответствующее возмущенной правой части . В дальнейшем будем считать, что . Это можно предположить, т.к. исследуется устойчивость по правой части.

Определим последовательность сеточных функций w_m(t) при t  t_m 1 согласно условиям:

(62)

Функции w_m, m = 0,1,2,… определены так, что w₀(t)  y(t) и при . Функции w_m(t) и w_m+1(t) на слое t_m совпадают по определению в (62). С учетом (61), (62) имеем

.

При t  t_m +1 функции w_m(t) и w_m+1(t) удовлетворяют разностной схеме с одной и той же правой частью , но с разными начальными данными на слое t_m +1. В силу равномерной устойчивости исходной разностной схемы по начальным данным можно сделать следующую оценку на последнем временном слое t_M:

.

Далее воспользуемся неравенством треугольника

Последняя цепочка неравенств доказывает утверждение теоремы об устойчивости по правой части.

В теории разностных схем рассматривается несколько способов исследования устойчивости:

• принцип максимума;

• метод разделения переменных;

• метод операторных неравенств

и некоторые другие.

Начнем с принципа максимума. Запишем двуслойную схему в следующем виде:

, (63)

где суммирование на каждом слое производится в пределах шаблона около n-го узла. Считаем, что коэффициенты _k таковы, что . В этом случае:

1. схема равномерно устойчива по начальным данным, когда

, C = const > 0; (64)

2. схема устойчива по правой части, если верно (64) и

,  = const > 0. (65)

Доказательство. Докажем первую часть утверждения a). Фиксируем правую часть _n в (63) и возмущаем решение y на исходном слое. В этом случае ошибка на следующем слое удовлетворяет уравнению

,

т.е.

.

Последнее неравенство рассмотрим применительно к узлу , в котором достигает своего максимума, при этом в правой части заменим и их максимальными значениями, что только усилит неравенство. В итоге получим

,

или в другой форме

. (66)

Согласно (64), имеем

. (67)

Комбинируя (66), (67), получаем

,

что соответствует обеспечению достаточного признака устойчивости по начальным данным (60). Первая часть утверждения доказана.

Докажем вторую часть утверждения b). Возмутим в (63) правую часть, оставляя неизменным решение на нижнем слое, тогда

.

Из последнего равенства можно записать следующее неравенство

.

Аналогично предыдущей части доказательства, выберем узел , в котором возмущение на следующем шаге максимально и заменим соответствующие величины своими максимумами, тогда

.

Учитывая теперь (65), получаем

,

что, согласно (61), означает устойчивость по правой части. Вторая часть утверждения доказана.

Рассмотрим пример решения нестационарной краевой задачи для уравнения теплопроводности с постоянным коэффициентом теплопроводности:

(68)

Запишем неявную разностную схему (24) для задачи (68) на равномерной сетке:

(69)

Если переписать (69) в форме (63), то

(70)

Остальные коэффициенты в (70) равны нулю. Непосредственно можно проверить, что при любых соотношениях шагов  и h условие (65) выполнено во всех регулярных узлах, а условие (64) — во всех узлах сетки. Это означает, что схема (69) безусловно устойчива по начальным данным, правой части и краевым условиям.