Размещено на http://www.allbest.ru/

Министерство образования и науки Российской Федерации

Алтайский государственный технический университет

им. И.И. Ползунова

Кафедра «Высшей математики»

Типовой расчет по математической статистике

Вариант задания-7

Барнаул 2009

1. Содержание задания

гистограмма эмпирический корреляционный статистика

В качестве исходных данных предлагаются результаты опроса людей об их весе. X (в килограммах) и росте Y (в сантиметрах). Данные приводятся в приложении: таблица П4 содержит результаты опроса 100 человек, проживающих в Европе.

Для обработки этих данных в типовом расчёте требуется выполнить следующую работу:

1. Из предложенной генеральной совокупности объёма N = 100 сформировать выборку объёма п = 50 с помощью таблицы П6 случайных чисел.

2. Для величин X и F составить группированные ряды. На основании этих рядов построить полигоны, гистограммы относительных частот и графики эмпирических функций распределения для X и Y.

3. Вычислить точечные оценки: выборочные средние х^ср и у^ср; несмещённые выборочные средние квадратичные отклонения s_x и s_y

4. Проверить гипотезы о нормальном законе распределения случайных величин Х и Y при уровне значимости α = 0,05.

5. Найти доверительные интервалы для М[Х], M[Y], D[X], D[Y] с надёжностью γ= 0,95.

6. Составить корреляционную таблицу. Вычислить выборочный коэффициент корреляции r_в и проверить гипотезу об отсутствии корреляционной связи между X иY (о незначимости отклонения r_в от нуля).

7. Найти выборочные уравнения прямых линий регрессии Y на X и X на Y. Построить графики этих прямых на одном рисунке с наблюдаемыми точками (x_i y_i), i= 1,..., п и эмпирическими линиями регрессии.

2. Выполнение типового расчёта

1. Сформируем выборку объёма п= 50 из генеральной совокупности (X, Y) , представленной в таблице П4 приложения.

Для этого воспользуемся таблицей из 50-ти случайных чисел, полученных с помощью датчика случайных чисел. Эти числа указывают номера элементов, которые будут взяты из генеральной совокупности:

Таблица 1(случайные величины), Вариант 7

6	27	73	92	78	48	81	80	1	23
35	55	88	76	14	35	43	13	16	88
44	94	64	99	10	38	29	3	79	14
77	7	84	67	11	18	37	91	2	17
100	49	87	41	45	52	82	28	46	32

Выборочная совокупность приводится в таблице 2:

Таблица 2(выборочная совокупность)

xi	yi	xi	yi	xi	yi	xi	yi	xi	yi
63,6	164	83,4	178	77	181	63	162	74,8	181
76,5	174	85	175	90,3	188	86,8	187	70,6	178
62,7	152	76,7	178	80,7	177	75,5	177	73,3	160
79,1	173	87,9	185	62,2	165	89,9	186	80,7	180
79,4	176	76	179	66,6	166	81,7	185	78,1	172
81,9	190	64,8	165	88,7	190	75,3	174	75,9	182
62,7	168	78	175	75,6	168	69,9	168	71,6	165
65,9	166	63,7	155	92	194	82	175	91,4	197
84,5	188	82,8	188	89,2	184	74,9	190	76,2	181
77,6	174	76,7	178	76	179	72,7	174	87,4	184

Величина x_i - вес (в килограммах), a y_i - рост (в сантиметрах) i-ro человека.

2. Составим группированный ряд для величины X. Для этого определим наибольшее

x_max =92

x_min =62,2

и наименьшее значения величины X, встречающееся в выборке. Вычислим размах:

R_x= х_тах - x_min= 92-62,2=29,8

Весь промежуток [62,2; 92] изменения выборочных данных величины X , разобьём на r = 7 интервалов (следуя рекомендации (30.2), модуль 30, при п = 50).

Тогда шаг разбиения

h_x = R_x / r =29,8/7=4,26

Для того, чтобы шаг разбиения был удобным, возьмём его равным h_x =5. Тогда расширение промежутка разбиения составит (5 -4,257) • 7 = 5,2.

Определения границ интервалов [a_i-1, a_i) , i — 1, ... , 7, границы определяются так:

ai=а_i-1+h_х, i — 1, ...,7.

Затем для каждого i-ro интервала [a_i-1, a_i) определяется его середина х_i* по формуле:

х_i*= (a_i-1+ a_i)/2

С помощью таблицы 2 находятся частоты n_i - количество выборочных значений X, попавших в i-й интервал.

Результаты группировки выборочных значений для X сведём в таблицу 3:

Таблица 3

Номер интервала i	Интервалы [ai-1;ai)	Середины интервалов xi*	Частоты ni	Относительные частоты ni/n	Накопленные относительные частоты i∑j=1(ni/n)	ni/nhx
1	[60;65)	62,5	7	0,14	0,14	0,03
2	[65;70)	67,5	3	0,06	0,20	0,01
3	[70;75)	72,5	6	0,12	0,32	0,03
4	[75;80)	77,5	16	0,32	0,64	0,08
5	[80;85)	82,5	8	0,16	0,80	0,04
6	[85;90)	87,5	7	0,14	0,94	0,03
7	[90;95]	92,5	3	0,06	1,00	0,01
		n=	50

Используя полученные результаты для х_i* и n_i/n (столбец 3-й и 5-й), строим полигон относительных частот (рисунок 1);

используя столбец 2-й и 7-й, строим гистограмму относительных частот (рисунок 2);

используя столбец 3-й и 6-й, строим график эмпирической функции распределения (рисунок 3).

Рисунок 1

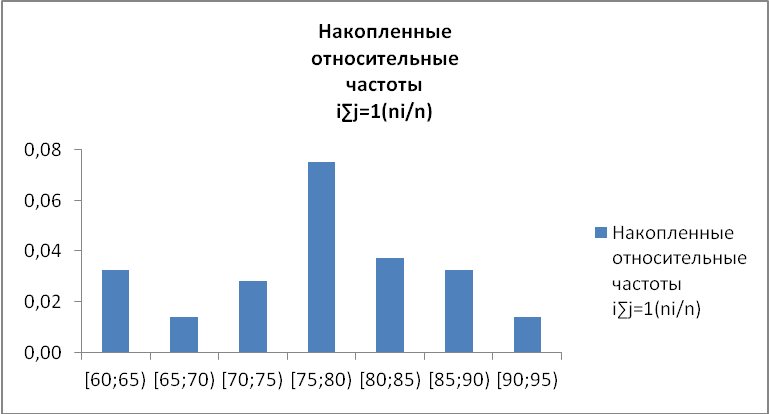
Рисунок 2

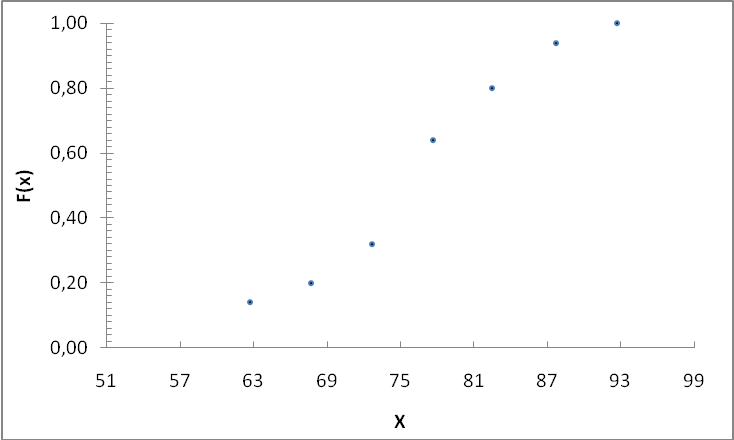
Рисунок 3

Для величины Y аналогичные результаты укажем в окончательном виде.

y_max=197

y_min=152

R_y=45

h_y=6,47=7

Результаты группировки выборочных значений для Y:

Таблица 4

Номер интервала i	Интервалы [bi-1;bi)	Середины интервалов yi*	Частоты mi	Относительные частоты mi/m	Накопленные относительные частоты i∑j=1(mi/m)	mi/mhy
1	[150;157)	153,5	2	0,04	0,04	0,01
2	[157;164)	160,5	2	0,04	0,08	0,01
3	[164;171)	167,5	9	0,18	0,26	0,03
4	[171;178)	174,5	12	0,24	0,50	0,04
5	[178;185)	181,5	13	0,26	0,76	0,04
6	[185;192)	188,5	9	0,18	0,94	0,03
7	[192;199]	195,5	3	0,06	1,00	0,01
		m=	50

На рисунках 4 - 6 изображены полигон, гистограмма относительных частот и график эмпирической функции распределения для величины Y:

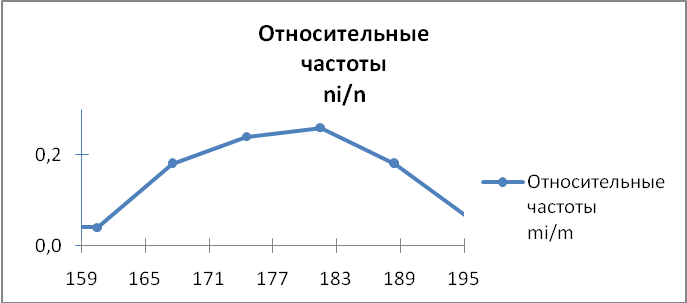
Рисунок 4

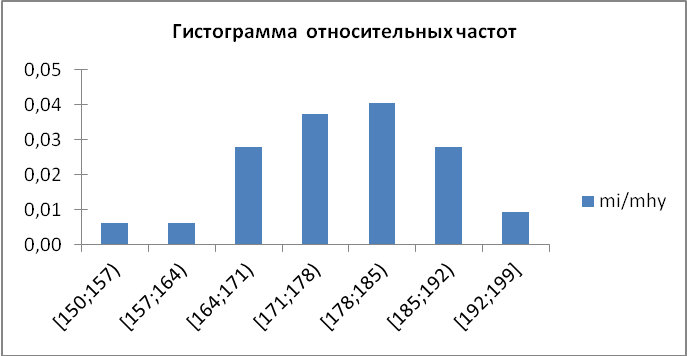
Рисунок 5

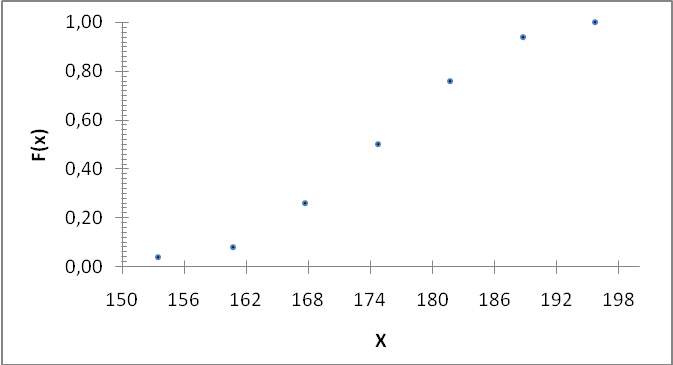
Рисунок 6

3. Точечные оценки х , у , sx , sy вычислим по группированным данным (см.Таблицы 3 и 4).

Составим таблицу 5:

Таблица 5

Номер интервала i	xi*	ni	xi*ni	xi*2ni	yi*	mi	yi*mi	yi*2mi
1	62,5	7	437,5	27343,75	153,5	2	307	47124,5
2	67,5	3	202,5	13668,75	160,5	2	321	51520,5
3	72,5	6	435	31537,5	167,5	9	1507,5	252506,3
4	77,5	16	1240	96100	174,5	12	2094	365403
5	82,5	8	660	54450	181,5	13	2359,5	428249,3
6	87,5	7	612,5	53593,75	188,5	9	1696,5	319790,3
7	92,5	3	277,5	25668,75	195,5	3	586,5	114660,8
∑	-	50	3865	302362,5	-	50	8872	1579254,5

Искомые оценки:

xср	77,3		yср	177,44
s2x	73,43		s2y	102,18
sx	8,57		sy	10,11

4. Проверим с помощью критерия χ2 гипотезу Но: распределение генеральной совокупности X имеет нормальный закон n(mx σx).

Здесь k = 2 неизвестных параметра m_x и σ_x (математическое ожидание и среднее квадратичное отклонение) заменяются соответствующими оценками x_ср =77,3 и s_x = 8,57

В качестве интервалов возьмём вначале интервалы [a_i-1, a_i), i = 1, ... ,7 (см. таблицу 3), приняв a₀= - ∞ , a₇=+∞ .

Результаты расчётов выборочной величины χ_В² приведём в таблице 6:

Таблица 6

[ai-1;ai)	ni	zi=(ai- xcp)/sx	Ф(zi)	pi=Ф(zi)-Ф(zi-1)	npi	(ni-npi)2/npi
(-∞;65)	7	-2,02	-0,478	0,022	1,10	0,1152
[65;70)	3	-1,32	-0,407	0,071	3,55
[70;75)	6	-0,62	-0,232	0,175	8,75	0,8643
[75;80)	16	0,08	0,032	0,264	13,20	2,2139
[80;85)	8	0,78	0,282	0,250	12,50
[85;90)	7	1,48	0,430	0,148	7,40	0,0931
[90;+∞)	3	∞	0,500	0,070	3,50
				1,000	50	3,29

Пришлось произвести объединение первых двух интервалов, 4 и 5, 6 и 7 из-за малости теоретических частот и для удовлетворения условия np_i> 5.

В итоге число интервалов т = 4, поэтому число степеней свободы для χ² распределения равно

т —k—1=4 —2 — 1 =1.

По таблице П2 приложения находим

j χ²_0,95(1) = 3,84.

Вывод: так как χ²_В= 3,29< χ²_0,95(1) = 3,84, то гипотеза Н_о о нормальном распределении величины X не противоречит выборочным данным.

Аналогично проверяем гипотезу Н_о: распределение генеральной совокупности Y имеет нормальный закон N(m_y σ_y).

Параметры т_у и σ_y заменяем соответственно оценками y^ср = 177,44 и s_y = 10,11.

Используя интервалы [b_i-1;b_i) и частоты m_i = 1,...,7 из таблицы 4, проведём вычисление χ²_В, оформив таблицу 7

Таблица 7

i	[bi-1;bi)	mi	zi=(bi- ycp)/sy	Ф(zi)	pi=Ф(zi)-Ф(zi-1)	mpi	(mi-mpi)2/mpi
1	(-∞;157)	2	-1,53	-0,437	0,063	3,15	0,42
2	[157;164)	2	-0,93	-0,324	0,113	5,65	2,778
3	[164;171)	9	-0,34	-0,133	0,191	9,55
4	[171;178)	12	0,25	0,099	0,232	11,60	0,814
5	[178;185)	13	0,85	0,302	0,203	10,15
6	[185;192)	9	1,44	0,425	0,123	6,15	1,471
7	[192;+∞)	3	∞	0,500	0,075	3,75
					1,000	50	5,48

Здесь объединены 2 и 3, 4 и 5, 6 и 7 интервалы, из-за малости теоретических частот.

В итоге число интервалов т = 4, поэтому число степеней свободы для χ² распределения равно

т —k—1=4 —2 — 1 =1.

По таблице П2 приложения находим

j χ²_0,95(2) = 5,99.

Вывод: так как χ²_В= 5,48< χ²_0,95(2) = 5,99, то гипотеза Н_о о нормальном распределении величины Y не противоречит выборочным данным.