Решение:

Преподаватель: Харасахал Л.А.  Специальность: 080100.62 - Экономика  Группа: 101 10  Дисциплина: Линейная алгебра  Идентификатор студента: 6) Иванова Арина Андреевна  Логин: 01ps1018498  Начало тестирования: 2013-04-23 17:14:26  Завершение тестирования: 2013-04-23 17:37:37  Продолжительность тестирования: 23 мин.  Заданий в тесте: 8  Кол-во правильно выполненных заданий: 3  Процент правильно выполненных заданий: 37 %

  ЗАДАНИЕ N 1 отправить сообщение разработчикам Тема: Прямоугольные координаты в пространстве В треугольнике с вершинами     и   проведена медиана AM, длина которой равна …

			7
			49

Решение: Точка M является серединой отрезка BC. Координаты середины отрезка определяются по формулам       Подставляя в эти формулы координаты точек   и   получим координаты точки M:       Расстояние между точками A и M можно найти по формуле  то есть 

  ЗАДАНИЕ N 2 отправить сообщение разработчикам Тема: Плоскость в пространстве, Общее уравнение плоскости, проходящей через точку   перпендикулярно прямой   имеет вид …

Решение: Уравнение плоскости, проходящей через точку   с нормальным вектором   имеет вид  Так как эта плоскость перпендикулярна прямой   то в качестве нормального вектора плоскости можно использовать направляющий вектор этой прямой, то есть   Тогда  или 

  ЗАДАНИЕ N 3 отправить сообщение разработчикам Тема: Прямая линия в пространстве В треугольнике с вершинами     и   проведена медиана AM. Тогда уравнение медианы может иметь вид …

Решение: Точка   является серединой отрезка   Координаты середины отрезка определяются по формулам       Подставляя в эти формулы координаты точек   и   получим координаты точки          Уравнение  прямой, проходящей через точки   и   имеет вид   Тогда уравнение медианы AM имеет вид 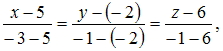  или 

 ЗАДАНИЕ N 4 отправить сообщение разработчикам Тема: Поверхности второго порядка Линия пересечения поверхности   и плоскости   представляет собой …

			параболу
			эллипс
			гиперболу
			окружность

 ЗАДАНИЕ N 5 отправить сообщение разработчикам Тема: Определение линейного пространства Для элементов линейного пространства операции сложения и умножения на действительное число обладают свойством …

 ЗАДАНИЕ N 6 отправить сообщение разработчикам Тема: Базис и размерность линейного пространства Совокупность векторов       не может являться базисом трехмерного линейного пространства, если   равно …

			1
			4
			2
			3

  ЗАДАНИЕ N 7 отправить сообщение разработчикам Тема: Линейные отображения Прообразом вектора   при линейном преобразовании, заданном матрицей   является вектор …

Решение: Так как   то 

  ЗАДАНИЕ N 8 отправить сообщение разработчикам Тема: Линейные операторы Пусть   – базис пространства   Операторы f и g этого пространства заданы матрицами     Тогда матрица оператора   равна …