Решение:

Преподаватель: Харасахал Л.А.  Специальность: 080100.62 - Экономика  Группа: 101 10  Дисциплина: Линейная алгебра  Идентификатор студента: 22) Попова Александра Олеговна  Логин: 01ps1018514  Начало тестирования: 2013-04-21 16:58:04  Завершение тестирования: 2013-04-21 17:33:24  Продолжительность тестирования: 35 мин.  Заданий в тесте: 8  Кол-во правильно выполненных заданий: 6  Процент правильно выполненных заданий: 75 %

 ЗАДАНИЕ N 1 отправить сообщение разработчикам Тема: Прямоугольные координаты в пространстве Даны точки   и   Тогда координаты точки  , симметричной точке B относительно точки A, равны …

 ЗАДАНИЕ N 2 отправить сообщение разработчикам Тема: Плоскость в пространстве, Расстояние от точки   до плоскости   равно …

			2,5
			6
			2
			3,1

 ЗАДАНИЕ N 3 отправить сообщение разработчикам Тема: Прямая линия в пространстве Точка пересечения прямой   и плоскости   имеет координаты …

  ЗАДАНИЕ N 4 отправить сообщение разработчикам Тема: Поверхности второго порядка Центр поверхности   …

			лежит в плоскости
			лежит в плоскости
			лежит в плоскости
			не лежит ни в одной из координатных плоскостей

Решение: Преобразуем данное уравнение поверхности. Для этого дополним до полных квадратов члены, содержащие   то есть перепишем уравнение в виде Тогда  или   Разделив обе части последнего уравнения на 36, получаем уравнение   которое определяет эллипсоид с центром в точке с координатами   то есть центр поверхности лежит в плоскости 

 ЗАДАНИЕ N 5 отправить сообщение разработчикам Тема: Определение линейного пространства Среди представленных множеств линейное пространство образует множество …

			всех векторов, принадлежащих пространству
			всех векторов пространства   образующих острый угол с положительным направлением оси ординат
			натуральных чисел
			всех отрицательных вещественных чисел

 ЗАДАНИЕ N 6 отправить сообщение разработчикам Тема: Базис и размерность линейного пространства Вектор   является линейной комбинацией векторов   и   Если   то   равно …

			2
			3
			– 2
			– 3

  ЗАДАНИЕ N 7 отправить сообщение разработчикам Тема: Линейные отображения Дано линейное преобразование векторов на плоскости Oxy, которое каждый вектор переводит в сонаправленный вектор, в два раза длиннее исходного. Тогда матрица Aэтого преобразования имеет вид …

			2

Решение: Так как   и   то матрица такого линейного преобразования имеет вид 

 ЗАДАНИЕ N 8 отправить сообщение разработчикам Тема: Линейные операторы Из заданных операторов пространства   – пространства двумерных векторов, линейным является оператор …

Преподаватель: Харасахал Л.А.  Специальность: 080100.62 - Экономика  Группа: 101 10  Дисциплина: Линейная алгебра  Идентификатор студента: 22) Попова Александра Олеговна  Логин: 01ps1018514  Начало тестирования: 2013-04-21 16:58:04  Завершение тестирования: 2013-04-21 17:33:24  Продолжительность тестирования: 35 мин.  Заданий в тесте: 8  Кол-во правильно выполненных заданий: 6  Процент правильно выполненных заданий: 75 %

 ЗАДАНИЕ N 1 отправить сообщение разработчикам Тема: Прямоугольные координаты в пространстве Даны точки   и   Тогда координаты точки  , симметричной точке B относительно точки A, равны …

 ЗАДАНИЕ N 2 отправить сообщение разработчикам Тема: Плоскость в пространстве, Расстояние от точки   до плоскости   равно …

			2,5
			6
			2
			3,1

 ЗАДАНИЕ N 3 отправить сообщение разработчикам Тема: Прямая линия в пространстве Точка пересечения прямой   и плоскости   имеет координаты …

  ЗАДАНИЕ N 4 отправить сообщение разработчикам Тема: Поверхности второго порядка Центр поверхности   …

			лежит в плоскости
			лежит в плоскости
			лежит в плоскости
			не лежит ни в одной из координатных плоскостей

Решение: Преобразуем данное уравнение поверхности. Для этого дополним до полных квадратов члены, содержащие   то есть перепишем уравнение в виде Тогда  или   Разделив обе части последнего уравнения на 36, получаем уравнение   которое определяет эллипсоид с центром в точке с координатами   то есть центр поверхности лежит в плоскости 

 ЗАДАНИЕ N 5 отправить сообщение разработчикам Тема: Определение линейного пространства Среди представленных множеств линейное пространство образует множество …

			всех векторов, принадлежащих пространству
			всех векторов пространства   образующих острый угол с положительным направлением оси ординат
			натуральных чисел
			всех отрицательных вещественных чисел

 ЗАДАНИЕ N 6 отправить сообщение разработчикам Тема: Базис и размерность линейного пространства Вектор   является линейной комбинацией векторов   и   Если   то   равно …

			2
			3
			– 2
			– 3

  ЗАДАНИЕ N 7 отправить сообщение разработчикам Тема: Линейные отображения Дано линейное преобразование векторов на плоскости Oxy, которое каждый вектор переводит в сонаправленный вектор, в два раза длиннее исходного. Тогда матрица Aэтого преобразования имеет вид …

			2

Решение: Так как   и   то матрица такого линейного преобразования имеет вид 

 ЗАДАНИЕ N 8 отправить сообщение разработчикам Тема: Линейные операторы Из заданных операторов пространства   – пространства двумерных векторов, линейным является оператор …

Преподаватель: Харасахал Л.А.  Специальность: 080100.62 - Экономика  Группа: 101 10  Дисциплина: Линейная алгебра  Идентификатор студента: 27) Солодухина Ольга Дмитриевна  Логин: 01ps1018519  Начало тестирования: 2013-04-17 14:17:49  Завершение тестирования: 2013-04-23 16:53:29  Продолжительность тестирования: 8795 мин.  Заданий в тесте: 8  Кол-во правильно выполненных заданий: 1  Процент правильно выполненных заданий: 12 %

  ЗАДАНИЕ N 1 отправить сообщение разработчикам Тема: Прямоугольные координаты в пространстве Точка   расстояние которой от точки  равно 12, лежит на оси абсцисс. Тогда отрицательные координаты точки M равны …

Решение: Так как точка   лежит на оси   то ее ордината   и аппликата   Расстояние от точки   до   равно 12. Тогда   или     то есть   

  ЗАДАНИЕ N 2 отправить сообщение разработчикам Тема: Плоскость в пространстве, Общее уравнение плоскости, проходящей через точку   перпендикулярно прямой   имеет вид …

Решение: Уравнение плоскости, проходящей через точку   с нормальным вектором   имеет вид  Так как эта плоскость перпендикулярна прямой   то в качестве нормального вектора плоскости можно использовать направляющий вектор этой прямой, то есть   Тогда  или 

  ЗАДАНИЕ N 3 отправить сообщение разработчикам Тема: Прямая линия в пространстве Параметрические уравнения прямой, параллельной оси Oy и проходящей через точку   имеют вид …

Решение: Параметрические уравнения прямой, проходящей через точку   с направляющим вектором   имеют вид  За направляющий вектор прямой можно взять  Тогда   или 

  ЗАДАНИЕ N 4 отправить сообщение разработчикам Тема: Поверхности второго порядка Каноническое уравнение линии пересечения однополостного гиперболоида   и плоскости   имеет вид …

Решение: Уравнение кривой пересечения однополостного гиперболоида и плоскости получим, решив систему   то есть   или  Полученное уравнение есть каноническое уравнение гиперболы.

 ЗАДАНИЕ N 5 отправить сообщение разработчикам Тема: Определение линейного пространства Линейное пространство L не обладает свойством …

			для любого   может существовать несколько противоположных элементов
			для любого
			для любого
			нейтральный элемент   является единственным

  ЗАДАНИЕ N 6 отправить сообщение разработчикам Тема: Базис и размерность линейного пространства Совокупность векторов       можно принять за базис трехмерного линейного пространства, если   равно …

			5
			–1
			3
			–2

Решение: Совокупность линейно независимых векторов называется базисом линейного этого пространства. Значит, совокупность трех векторов является базисом, если векторы линейно независимы, то есть определитель, составленный из координат этих векторов,  не равен нулю. Тогда

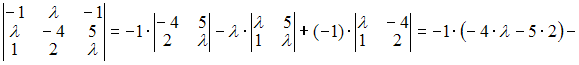
  ЗАДАНИЕ N 7 отправить сообщение разработчикам Тема: Линейные отображения Дано линейное преобразование векторов на плоскости Oxy, которое каждый вектор переводит в вектор той же длины, но противоположно направленный исходному. Тогда матрица A этого преобразования имеет вид …

			–1

Решение: Так как   и   то матрица такого линейного преобразования имеет вид 

  ЗАДАНИЕ N 8 отправить сообщение разработчикам Тема: Линейные операторы Линейный оператор f отображает базис   в векторы      Тогда матрица оператора   в этом базисе имеет вид …