Преподаватель: Харасахал Л.А.  Специальность: 080100.62 - Экономика  Группа: 103 10  Дисциплина: Линейная алгебра  Идентификатор студента: 11) Воржева Екатерина Михайловна  Логин: 01ps1018568  Начало тестирования: 2013-04-21 11:06:56  Завершение тестирования: 2013-04-21 11:14:42  Продолжительность тестирования: 7 мин.  Заданий в тесте: 8  Кол-во правильно выполненных заданий: 2  Процент правильно выполненных заданий: 25 %

  ЗАДАНИЕ N 1 отправить сообщение разработчикам Тема: Прямоугольные координаты в пространстве Точки   и   лежат симметрично относительно плоскости XOY. Расстояние между ними равно 6. Тогда точки A и B могут иметь координаты …

Решение: Так как точки   и   симметричны относительно плоскости XOY, то они имеют координаты   и     то есть   Этому условию удовлетворяют координаты точек   и 

  ЗАДАНИЕ N 2 отправить сообщение разработчикам Тема: Плоскость в пространстве, Плоскости   и   …

			перпендикулярны
			параллельны
			пересекаются под острым углом
			совпадают

Решение: Найдем угол между этими плоскостями. Угол, образованный двумя плоскостями   и   определяется из соотношения  Тогда   или   то есть плоскости перпендикулярны.

 ЗАДАНИЕ N 3 отправить сообщение разработчикам Тема: Прямая линия в пространстве Параметрические уравнения прямой, параллельной оси Oy и проходящей через точку   имеют вид …

 ЗАДАНИЕ N 4 отправить сообщение разработчикам Тема: Поверхности второго порядка Уравнение поверхности второго порядка   определяет …

			эллипсоид
			параболоид
			конус
			однополостный гиперболоид

  ЗАДАНИЕ N 5 отправить сообщение разработчикам Тема: Определение линейного пространства Элементы линейного пространства   удовлетворяющие свойству   называются …

			противоположными
			нейтральными
			обратными
			ортогональными

Решение: Линейное пространство обладает свойством: для любого   противоположный элемент   является единственным.

  ЗАДАНИЕ N 6 отправить сообщение разработчикам Тема: Базис и размерность линейного пространства За базис трехмерного векторного пространства можно принять совокупность векторов …

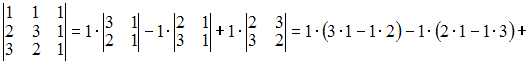
Решение: Если в линейном пространстве есть   линейно независимых векторов, а любые   векторы линейно зависимы, то пространство называется n-мерным, а совокупность линейно независимых векторов называется базисом линейного этого пространства. Значит, совокупность трех векторов должна быть линейно независимой, то есть определитель, составленный из координат этих векторов, не равен нулю. Тогда  Следовательно, совокупность векторов   можно принять за базис трехмерного пространства. Остальные совокупности векторов нельзя принять за базис трехмерного пространства, так как определители, составленные из координат этих векторов, равны нулю, то есть эти векторы линейно зависимы.

  ЗАДАНИЕ N 7 отправить сообщение разработчикам Тема: Линейные отображения Дано линейное преобразование векторов на плоскости Oxy, которое каждый вектор переводит в сонаправленный вектор, в два раза длиннее исходного. Тогда матрица Aэтого преобразования имеет вид …

			2

Решение: Так как   и   то матрица такого линейного преобразования имеет вид 

  ЗАДАНИЕ N 8 отправить сообщение разработчикам Тема: Линейные операторы Линейный оператор   отображает базис   в векторы      Тогда матрица оператора f в этом базисе имеет вид …

Решение:

Преподаватель: Харасахал Л.А.  Специальность: 080100.62 - Экономика  Группа: 101 10  Дисциплина: Линейная алгебра  Идентификатор студента: 4) Гузев Максим Владимирович  Логин: 01ps1018496  Начало тестирования: 2013-04-22 20:51:15  Завершение тестирования: 2013-04-22 20:55:10  Продолжительность тестирования: 3 мин.  Заданий в тесте: 8  Кол-во правильно выполненных заданий: 4  Процент правильно выполненных заданий: 50 %

 ЗАДАНИЕ N 1 отправить сообщение разработчикам Тема: Прямоугольные координаты в пространстве Даны точки   и  . Тогда координаты середины отрезка AB равны …

 ЗАДАНИЕ N 2 отправить сообщение разработчикам Тема: Плоскость в пространстве, Площадь треугольника, отсекаемого плоскостью   от координатного угла   равна …

			7,5
			2,5
			30
			15

 ЗАДАНИЕ N 3 отправить сообщение разработчикам Тема: Прямая линия в пространстве Направляющий вектор прямой   имеет вид …

  ЗАДАНИЕ N 4 отправить сообщение разработчикам Тема: Поверхности второго порядка Даны уравнения поверхностей второго порядка: А)  B)  C)  D)  Тогда эллипсоид задается уравнением …

			С
			В
			A
			D

Решение: Так как каноническое уравнение эллипсоида имеет вид   то искомое уравнение может иметь вид 

  ЗАДАНИЕ N 5 отправить сообщение разработчикам Тема: Определение линейного пространства Свойством линейного пространства L является …

Решение: Множество   образует линейное пространство, если для любых двух его элементов   определены операции сложения   и умножения на действительное число     со свойствами: 1.  2.  3.  4.  5.  6. 

 ЗАДАНИЕ N 6 отправить сообщение разработчикам Тема: Базис и размерность линейного пространства Совокупность векторов       не может являться базисом трехмерного линейного пространства, если   равно …

			1
			4
			2
			3

  ЗАДАНИЕ N 7 отправить сообщение разработчикам Тема: Линейные отображения Дано линейное преобразование векторов на плоскости Oxy, которое каждый вектор переводит в вектор той же длины, но противоположно направленный исходному. Тогда матрица A этого преобразования имеет вид …

			–1

Решение: Так как   и   то матрица такого линейного преобразования имеет вид 

  ЗАДАНИЕ N 8 отправить сообщение разработчикам Тема: Линейные операторы Линейный оператор   отображает базис   в векторы      Тогда матрица оператора f в этом базисе имеет вид …