3.3 Изгиб

Задача 3.1 Для балки с консольным защемлением, работающей на изгиб, требуется:

1. определить величины поперечной силы 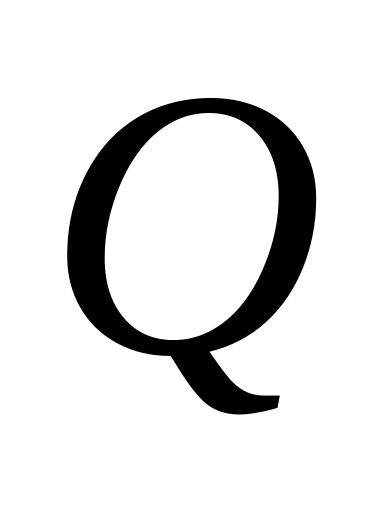и изгибающего момента 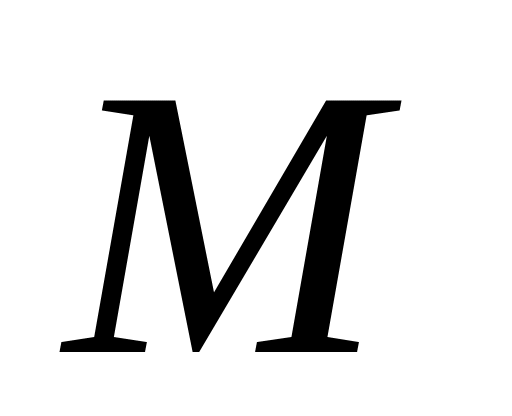на всех участках балки; построить эпюры соответствующих внутренних силовых факторов;

2. подобрать размеры поперечного сечения стальной балки для случаев: двутавровой; прямоугольного поперечного сечения; круглого поперечного сечения; кольцевого поперечного сечения; выбрать рациональное сечение, в зависимости от соотношения расходов материала на единицу длины балки;

3. выполнить чертежи всех вариантов поперечного сечения балки;

4. вычислить нормальные и касательные напряжения в характерных точках двутаврового сечения балки, построить эпюры соответствующих напряжений;

5. проверить балку двутаврового сечения по 3-й теории прочности.

Дано:

1. допускаемые напряжения для стали: нормальное напряжение 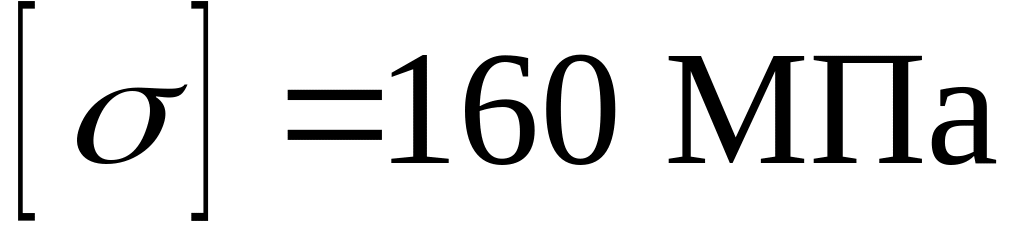; касательное напряжение ;

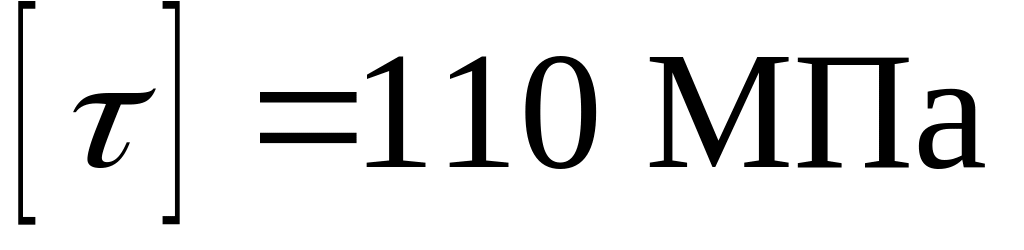2. внешние усилия ; ; ;

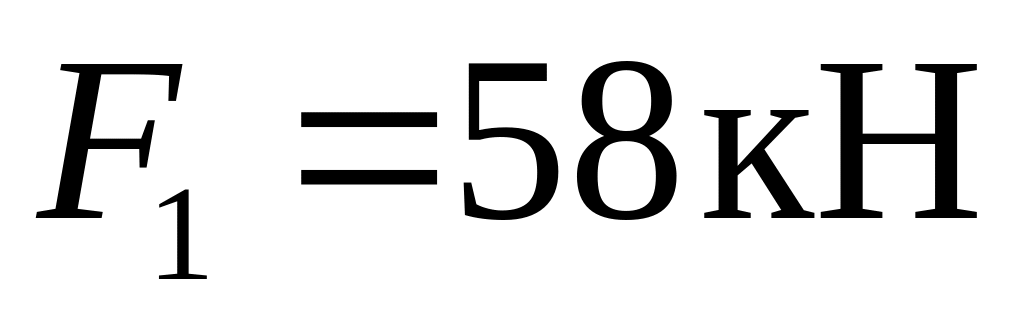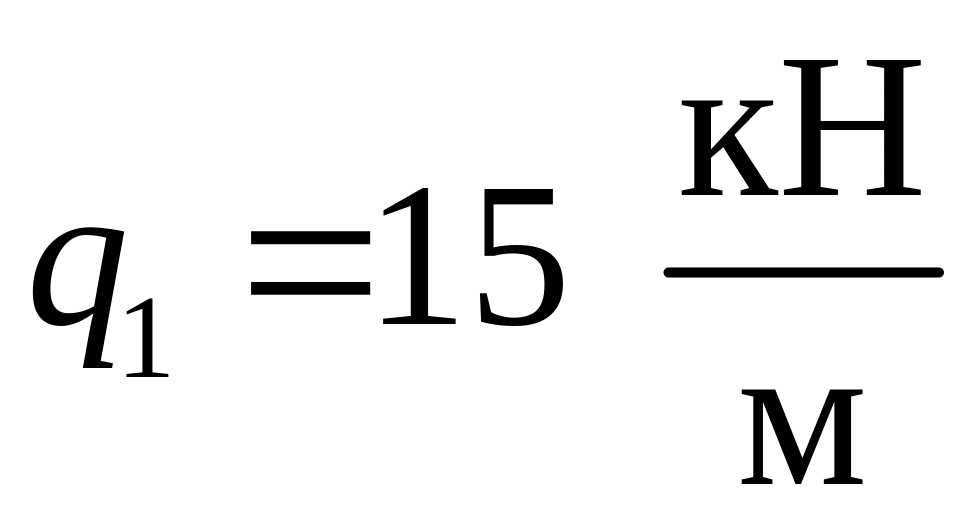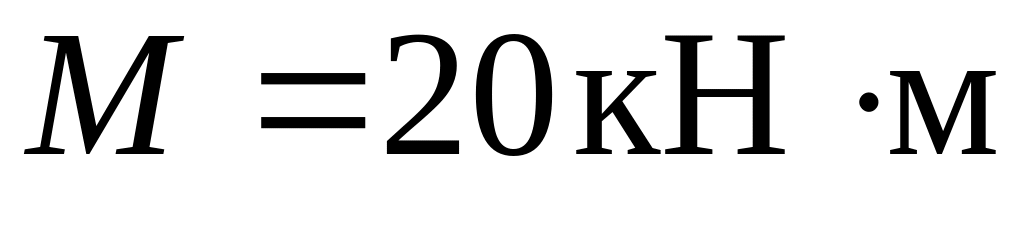3. длины участков ; ; ;

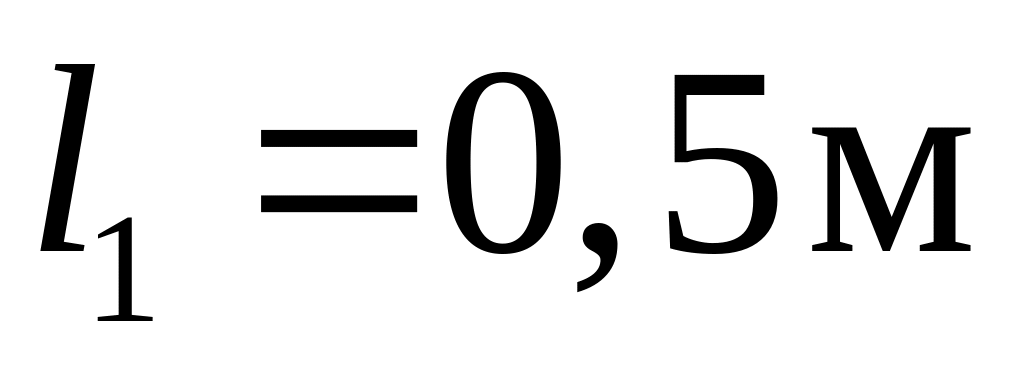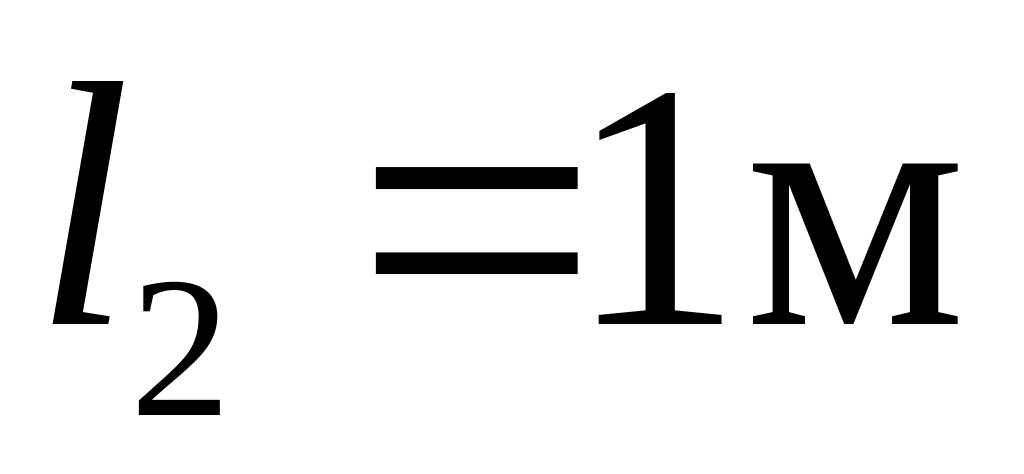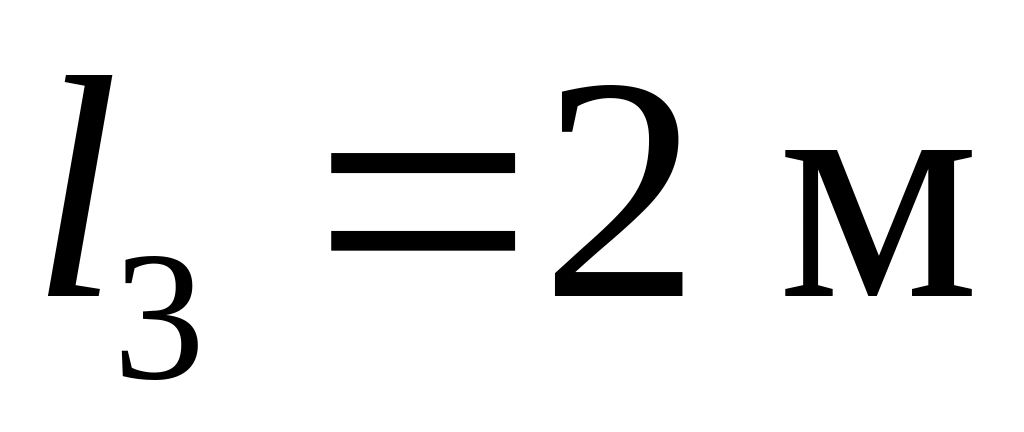4. отношение большей стороны 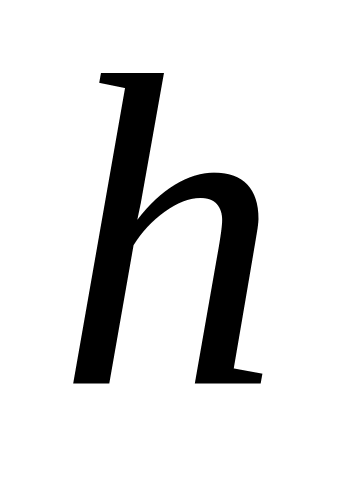к меньшей 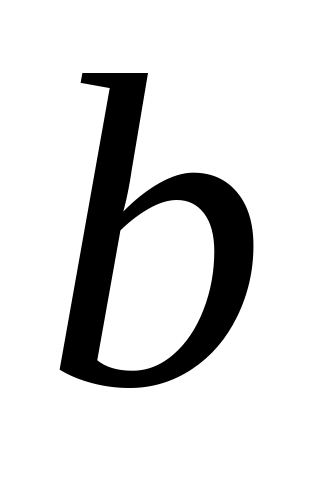прямоугольного сечения взять равным ;

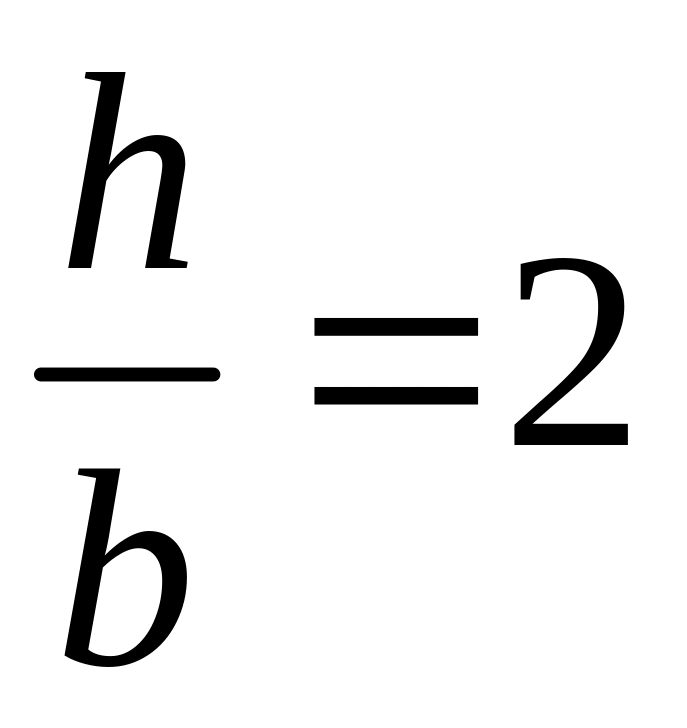5. в кольцевом сечении, соотношение внутреннего диаметра к наружному взять равным .

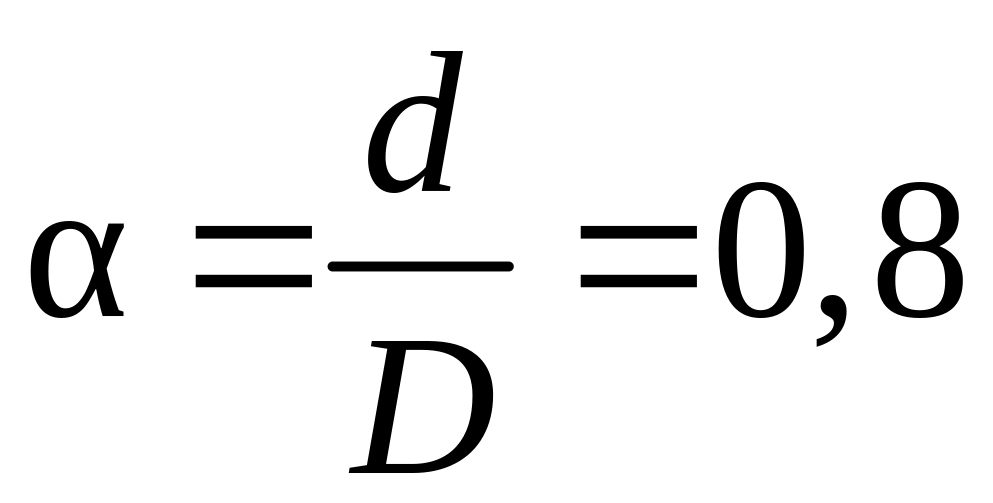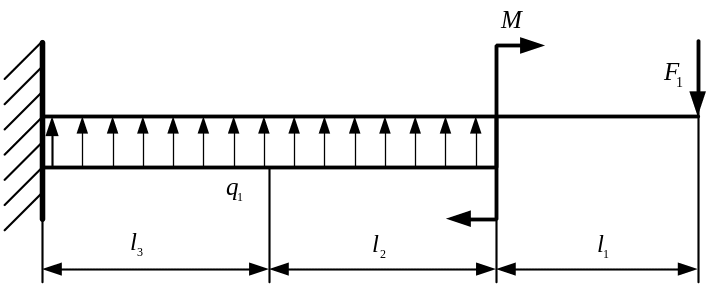
Рис. 3.1. Схема нагружения балки

Решение. 1. Для определения внутренних силовых факторов Q и M выполним сечения (рис. 3.) на участках балки начиная со свободного её конца в сторону жёсткого защемления.

Рассмотрим первый участок I-I (рис. 3.2). Его длина изменяется в пределе .

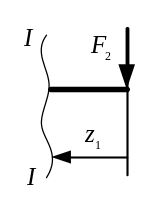
Рис. 3.2. Первый отсечённый участок

Поперечная сила определится по формуле:

.

Изгибающий момент будет равен:

.

Уравнение включает в себя переменную первой степени ( ). Следовательно, изгибающий момент будет переменным на первом участке. Определим его величину на границах участка:

при

при .

Рассмотрим второй участок II-II (рис. 3.2). Его длина изменяется в пределе .

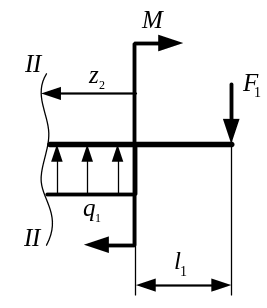
Рис. 3.3. Второй отсечённый участок

Поперечная сила определится по формуле:

.

Уравнение является уравнением первой степени. Определим поперечную силу на границах второго участка:

при ;

при .

Изгибающий момент на втором участке определится по уравнению:

.

Уравнение является уравнением второй степени, графиком которой является парабола. Следовательно, определим величину изгибающего момента на данном участке в трёх точках (в середине участка и на его границах), получим:

при

при

при .

Рассмотрим третий участок III-III (рис. 3.4). Его длина изменяется в пределе .

Поперечная сила определится по формуле:

.

Уравнение является уравнением первой степени. Определим поперечную силу на границах третьего участка:

при ;

при .

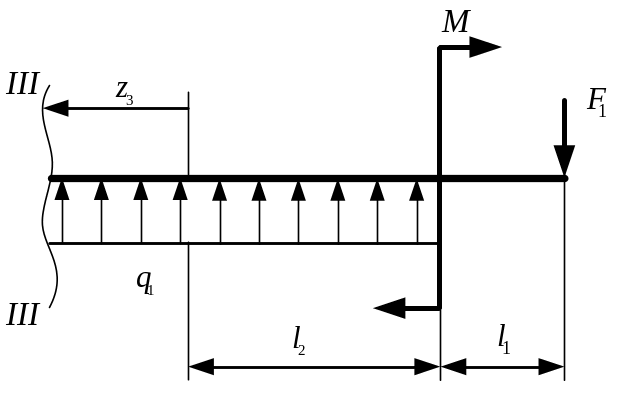
Рис. 3.4. Третий отсечённый участок

Изгибающий момент на третьем участке определится по уравнению:

.

Определим величину изгибающего момента в трёх точках (в середине участка и на его границах), получим:

при ;

при

при

По найденным величинам поперечной силы и изгибающего момента на участках балки, строим соответствующие эпюры (рис. 3.5) в выбранном масштабе.

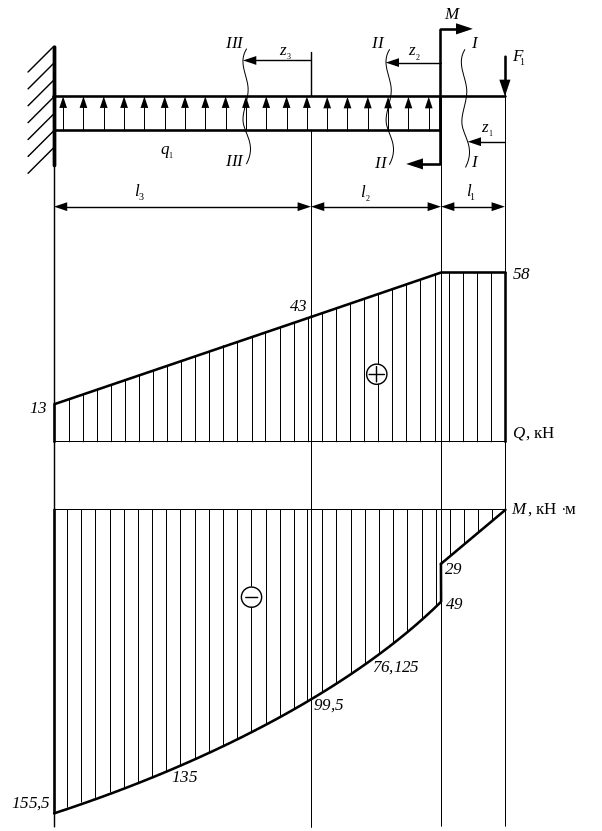
Рис. 3.4. Схема нагружения балки с эпюрами

2. Для определения размеров поперечного сечения балки различных профилей, воспользуемся условием прочности при изгибе, которое выглядит следующим образом:

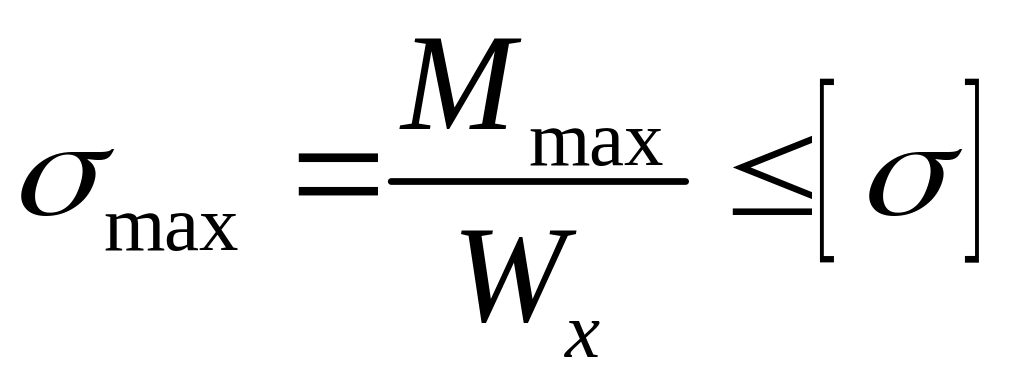, (3.1)

где   момент сопротивления сечения;   максимальное расчётное нормальное напряжение;   максимальный изгибающий момент.

В нашем примере максимальный изгибающий момент действует на третьем участке при .

Используя условие прочности (3.1), определим величину момента сопротивления сечения

.

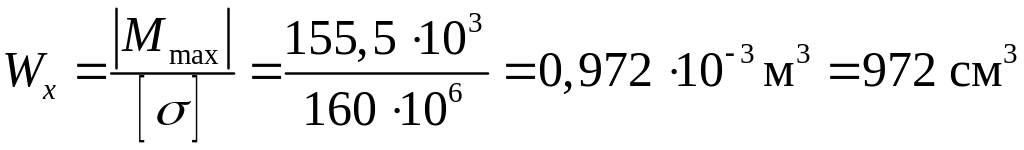Двутавровое сечение балки подбираем из таблиц сортамента прокатной стали (ГОСТ 8239-89). Полученной величине соответствует ближайшее значение , которое в свою очередь, соответствует двутавру №40, с площадью поперечного сечения .

Так как момент сопротивления принятого двутавра меньше чем расчетный, то необходимо определить перенапряжение, которое не должно превышать 5%.

Расчетное максимальное напряжение для выбранного двутавра будет равно:

.

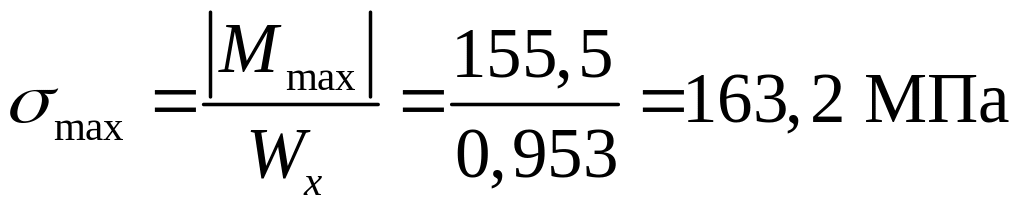Перенапряжение в данном случае составляет:

.

Так как перенапряжение не превышает допускаемую величину, выбранное сечение двутавра принимаем для дальнейших расчётов.

Для круглого поперечного сечения момент сопротивления определяется по зависимости:

(3.2)

Выразим из (3.2) диаметр сечения, получим:

.

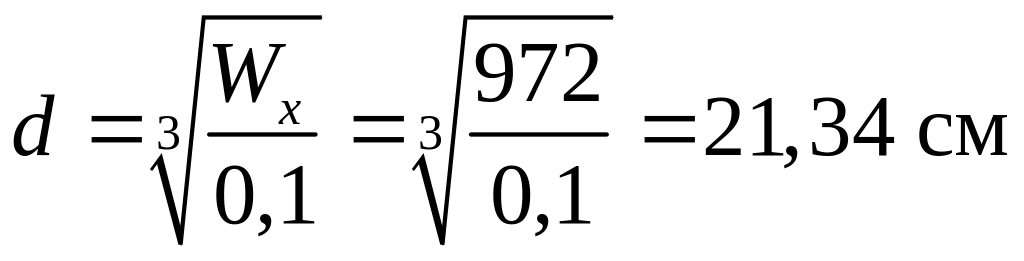Соответственно, площадь сечения будет равна:

.

Для кольцевого сечения момент сопротивления сечения определяется по формуле:

.

Тогда, наружный диаметр сечения определится по формуле:

.

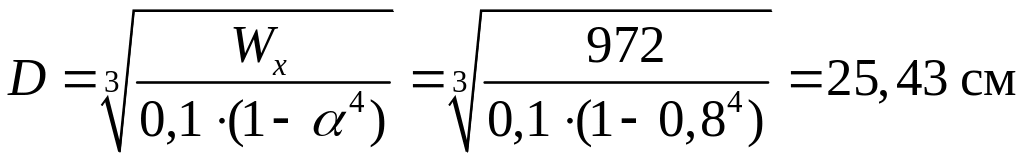Внутренний диаметр кольцевого сечения будет равен:

.

Зная величины наружного и внутреннего диаметров, определим площадь сечения:

Момент сопротивления прямоугольного сечения определяется по формуле:

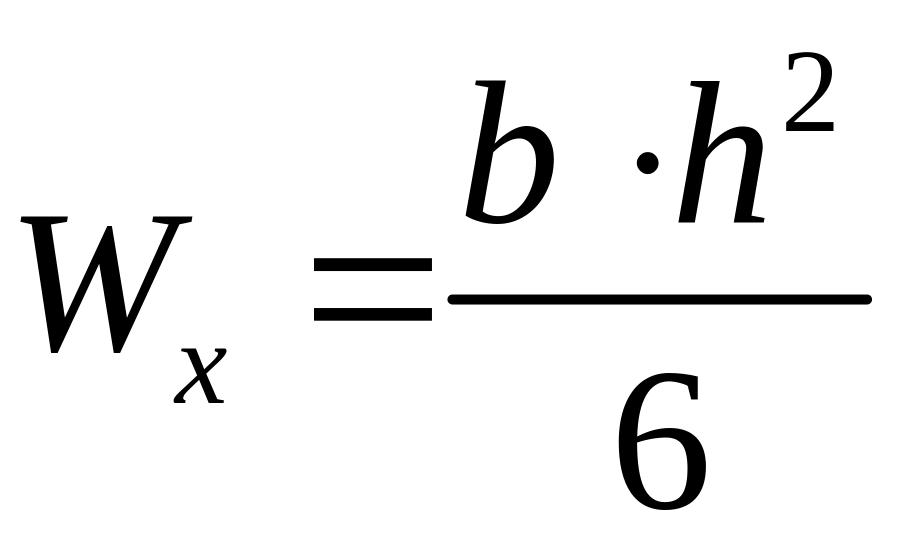. (3.3)

Зная величину соотношения сторон сечения ( ) выразим из формулы (3.3) ширину прямоугольника :

.

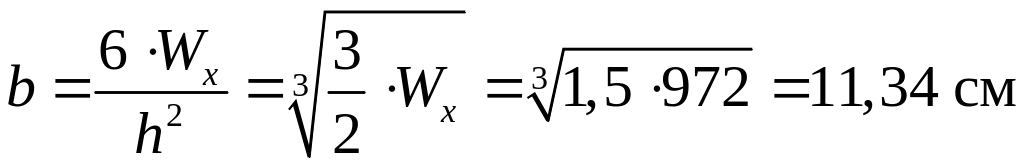Высота прямоугольника равна:

.

Зная геометрические параметры прямоугольного сечения, определим его площадь:

.

Наиболее рациональным сечением в зависимости от соотношения расходов материала на единицу длины балки будет являться сечение с минимальной площадью. Сравнивая значения площадей рассматриваемых сечений получаем, что наиболее рациональным является двутавровое ( ). Данное утверждение наглядно доказывается соотношением площадей. Приняв площадь двутавра за единицу площади, получаем следующие соотношения:

Наиболее нерациональным является круглое поперечное сечение.

3. По найденным геометрическим параметрам выполняем чертежи рассматриваемых сечений (рис. 3.5 а, б, в, г).

4. При прямом поперечном изгибе нормальные напряжения в произвольной точке поперечного сечения определяются по формуле:

,

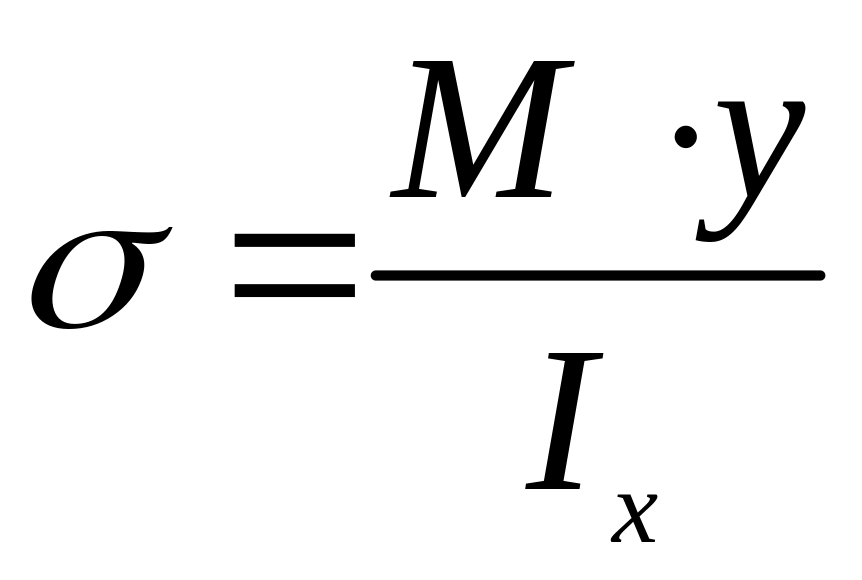где   изгибающий момент в рассматриваемом сечении; y  расстояние от нейтральной оси до точки, в которой определяется напряжение; I_x  осевой момент инерции сечения относительно нейтральной оси.

Запишем геометрические характеристики выбранного нами двутавра №40:

высота двутавра ; ширина полки ; толщина стенки ; средняя толщина полки ; площадь поперечного сечения  ; момент инерции ; моменты сопротивления , ; статический момент полусечения  ; радиус инерции .

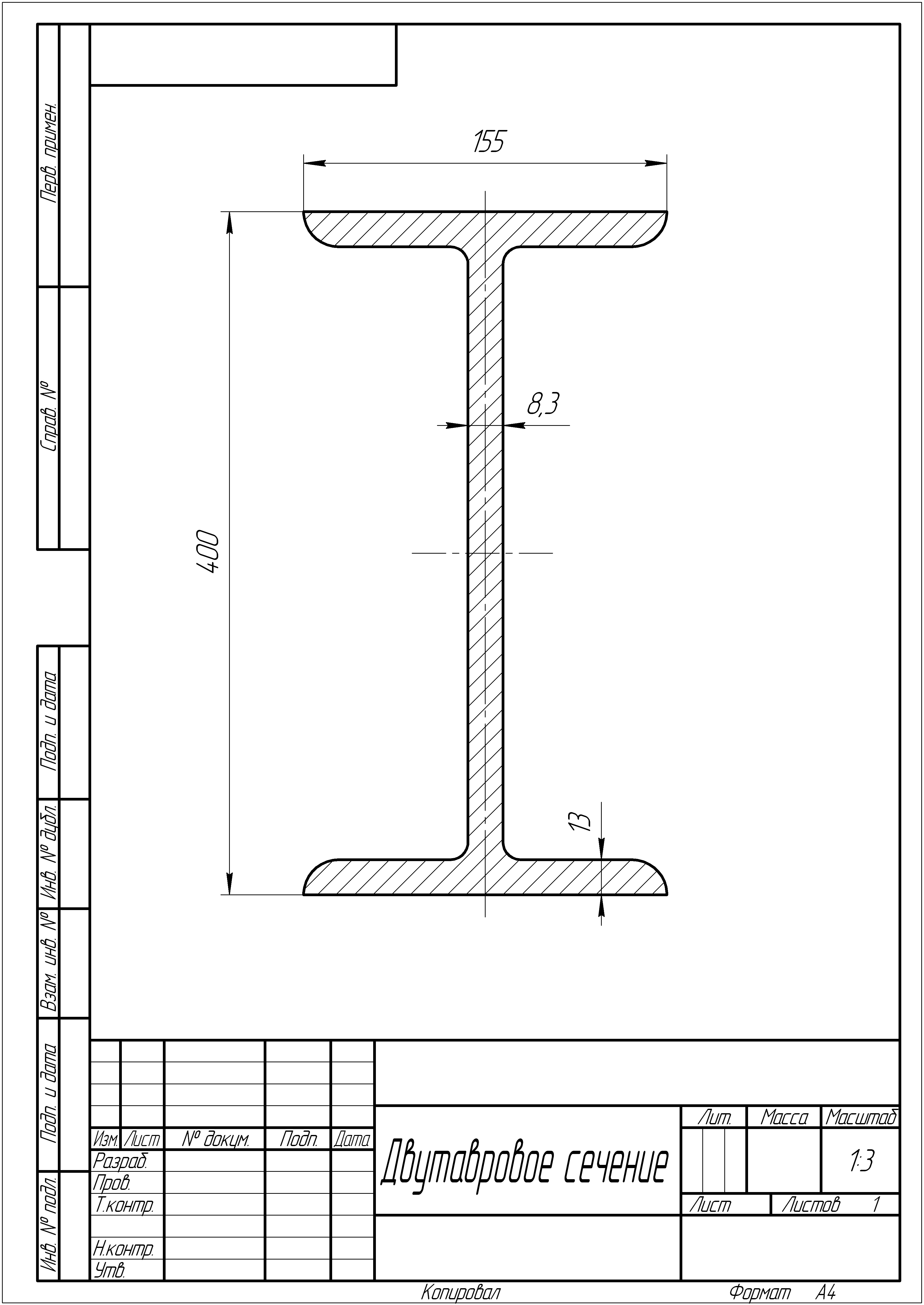
Рис. 3.5 а. Чертёж двутаврового сечения

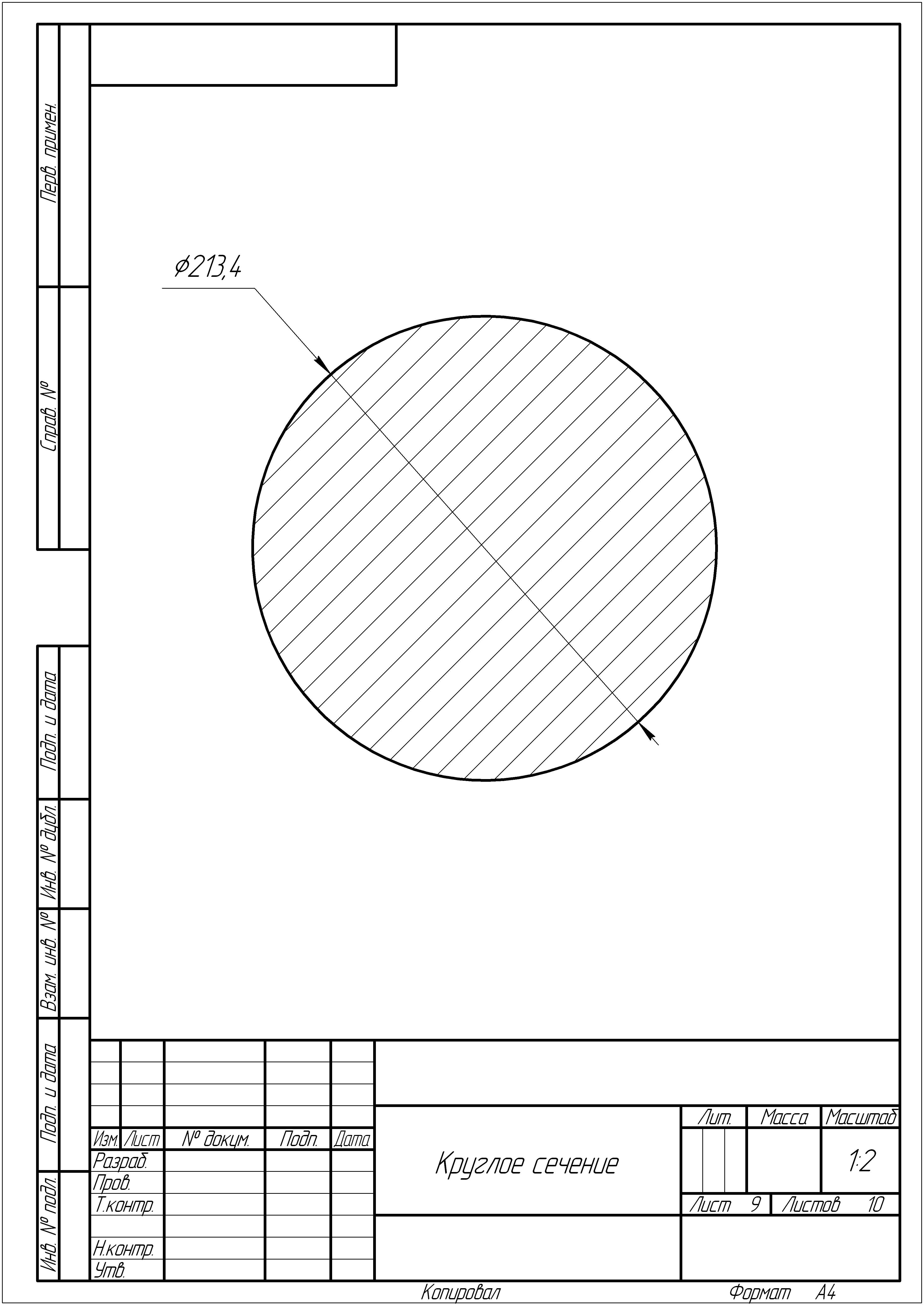
Рис. 3.5 б. Чертёж круглого поперечного сечения

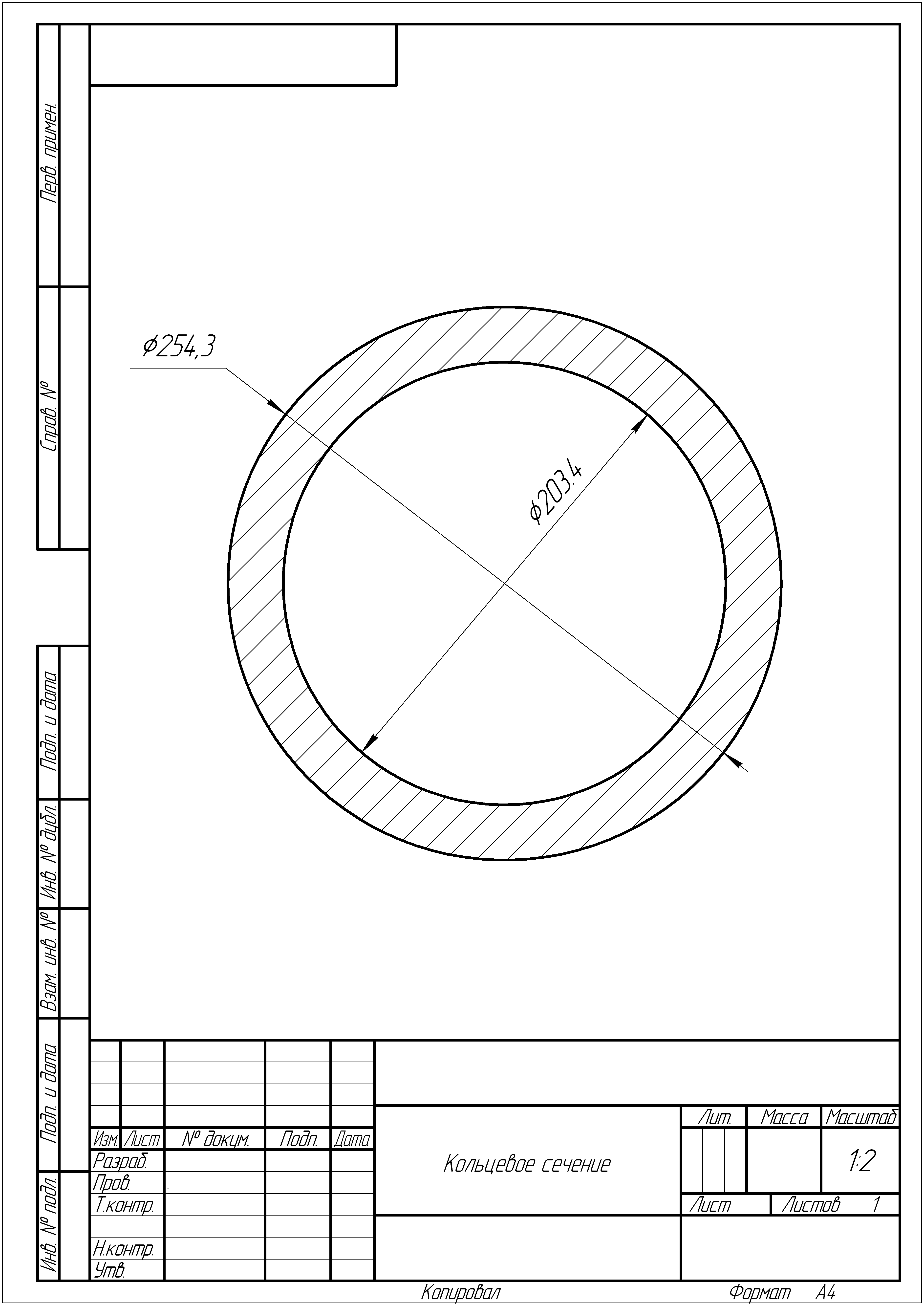
Рис. 3.5 а. Чертёж кольцевого сечения

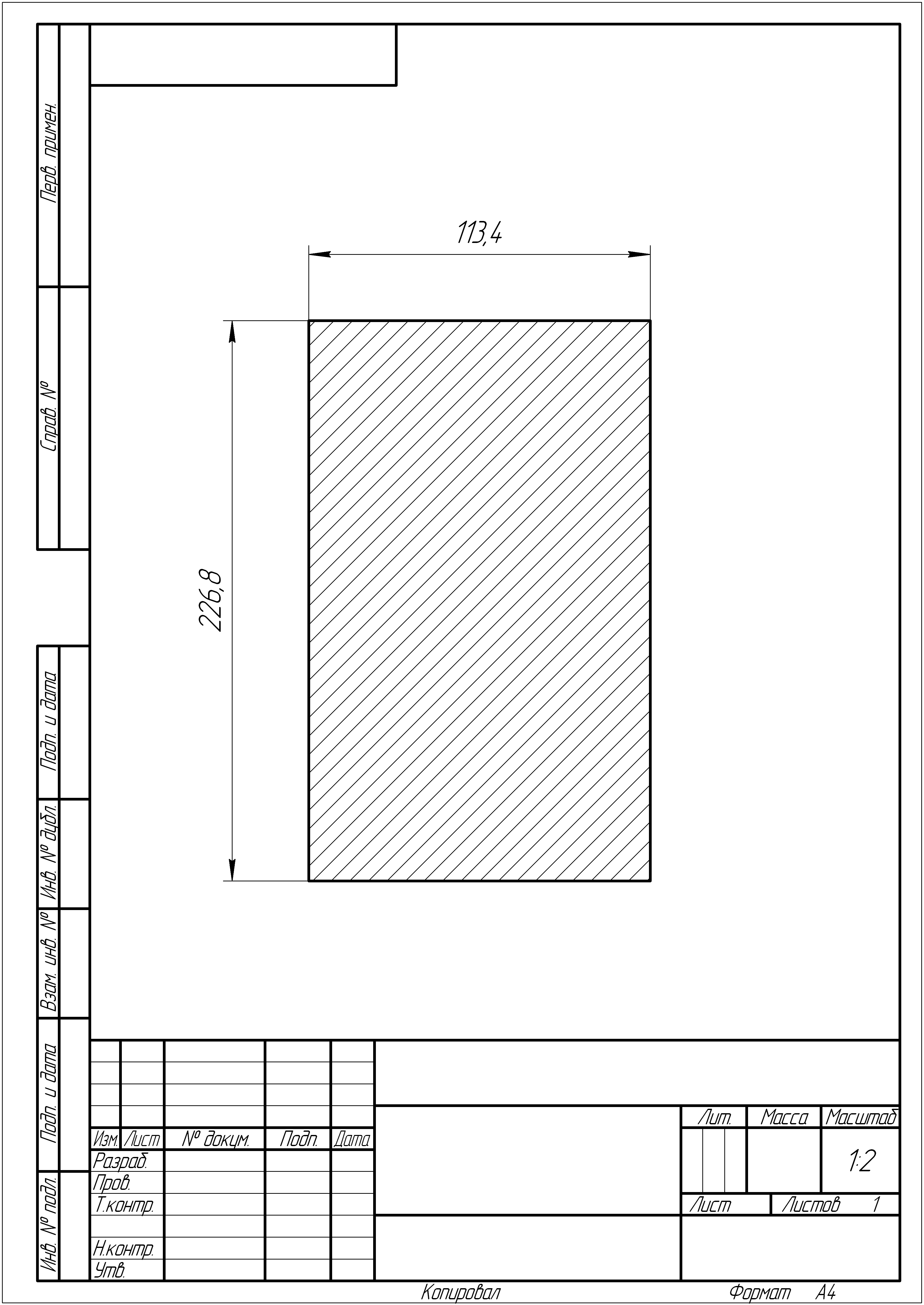
Рис. 3.5 а. Чертёж прямоугольного сечения

Расчёт нормальных и касательных напряжений будем проводить для сечений балки в которых имеется максимальные значения изгибающего момента и поперечной силы. В нашем случае ; .

Обозначим характерные точки по высоте двутаврового сечения, для которых будем определять величины напряжений (рис. 3.6).

В точке 1 ( ) нормальное напряжение будет равно:

.

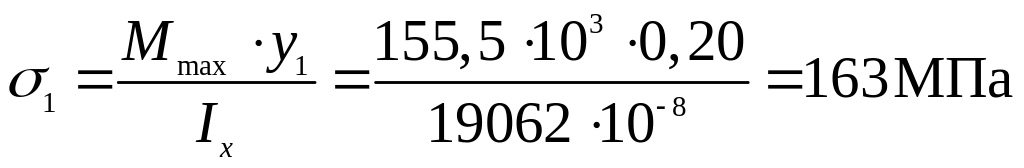Так как изгибающий момент в опасном сечении отрицательный, то точки 1 и 2 лежат в растянутой зоне, следовательно, напряжение в данных точках положительно.

Для точки 2 расстояние равно:

.

Определим величину напряжения в точке 2:

.

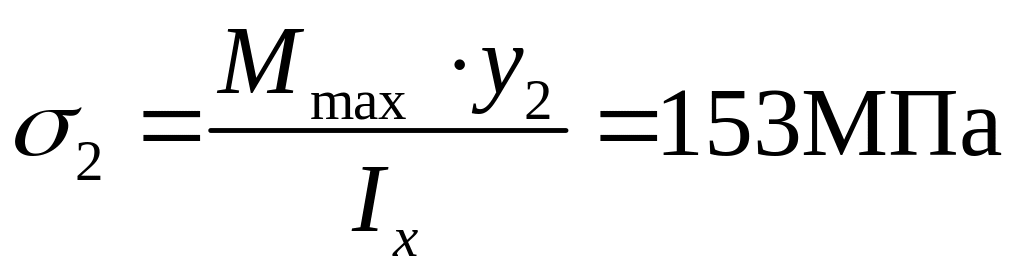Точка 3 лежит на нейтральной оси, поэтому расстояние , следовательно, нормальное напряжение тоже равно нулю ( ).

Точки 4 и 5 лежат в сжатой зоне сечения, поэтому напряжения в данных точках будет отрицательное, а их величины будут теми же самыми, что и в точках 2 и 1:

для точки 4 ;

для точки 5 .

Касательные напряжения при изгибе определяются по формуле:

,

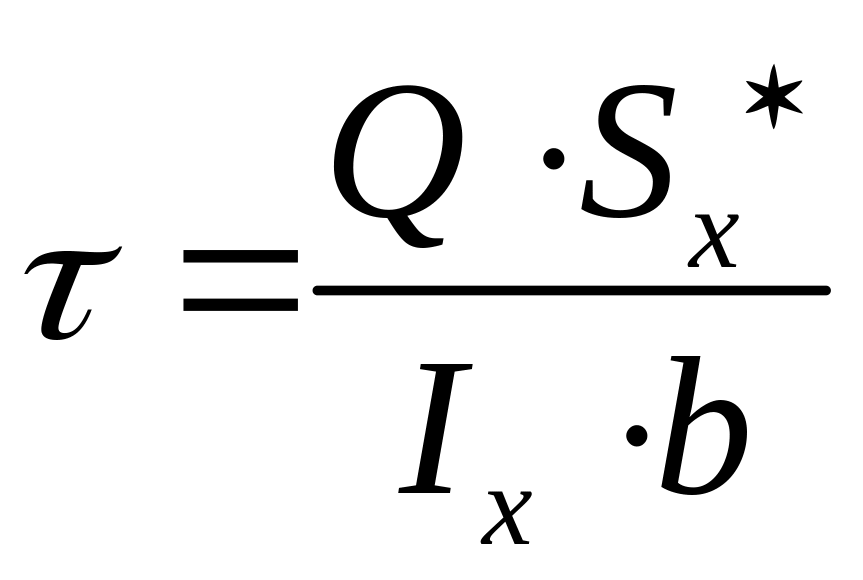где   поперечная сила в рассматриваемом сечении;   статический момент отсеченной части относительно нейтральной оси;   момент инерции всего сечения относительно нейтральной оси; b – ширина поперечного сечения на уровне рассматриваемой точки.

В свою очередь, статический момент отсеченной части площади сечения относительно нейтральной оси определяется по формуле:

,

где   площадь отсеченной часть сечения;    координата центра тяжести отсеченной площади.

Величина касательных напряжений в двутавровом сечении изменяется скачкообразно, так как ширина волокна переменна. А резкое изменение ширины сечения вызывает местное распределение напряжений.

Знак касательных напряжений совпадают со знаком поперечной силы.

В точках 1 и 5 статический момент равен нулю, так как нет площади отсечённой части. Следовательно, и напряжения в данных точках будут равняться нулю, т. е. .

В точках 2 и 4 отсечённые площади сечения одинаковы. Статический момент для них будет равен:

.

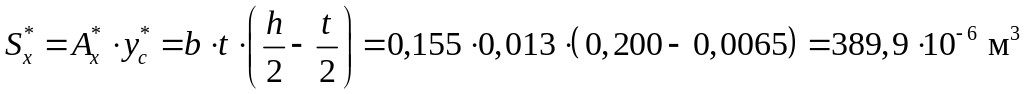Зная величину определим значения касательных напряжений:

при ;

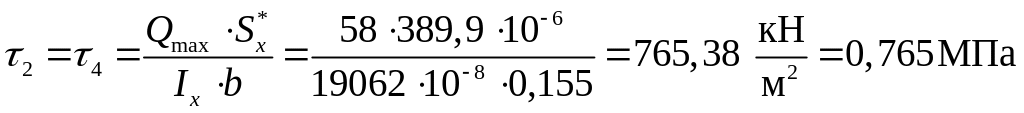при .

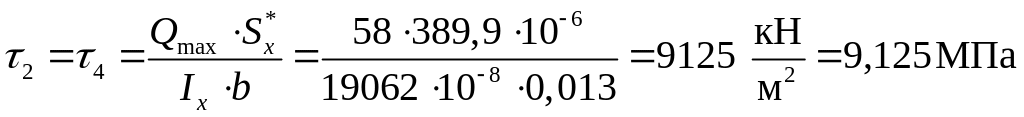В точке 3 значение статического момента берётся из справочника , а ширина поперечного сечения равна . Тогда касательное напряжение в этой точке будет равно:

.

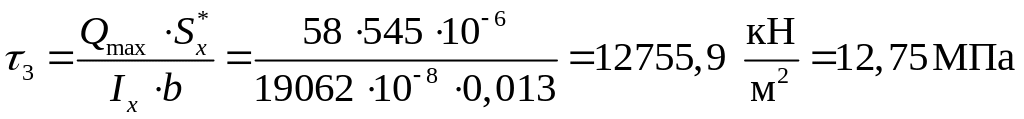По найденным величинам нормальных и касательных напряжений строим эпюры и (рис. 3.6).

Рис. 3.6. Эпюры напряжений.

Анализируя эпюры видно, что максимальное касательное напряжение имеет место на нейтральной линии ( ), максимальное нормальное напряжение  на границах двутаврового сечения ( ), т. е. в точках 1 и 5.

5. Условие прочности при изгибе по касательным напряжениям имеет вид:

. (3.4)

Для стальных балок по 3-й теории прочности допускаемое касательное напряжение принимаем равным:

.

В нашем случае, для балки двутаврового сечения будем иметь:

Следовательно, условие прочности выполняется.

Задание 3.1 Для балки с консольным защемлением, работающей на изгиб, требуется:

1. определить величины поперечной силы и изгибающего момента на всех участках балки; построить эпюры соответствующих внутренних силовых факторов;

2. подобрать размеры поперечного сечения стальной балки для случаев: двутавровой; прямоугольного поперечного сечения; круглого поперечного сечения; кольцевого поперечного сечения; выбрать рациональное сечение, в зависимости от соотношения расходов материала на единицу длины балки;

3. выполнить чертежи всех вариантов поперечного сечения балки;

4. вычислить нормальные и касательные напряжения в характерных точках двутаврового сечения балки, построить эпюры соответствующих напряжений;

5. проверить балку двутаврового сечения по 3-й теории прочности.

Схемы нагружения консольной балки взять на рис. 3.7, исходные данные к схемам взять в таблице 3.1.

Задача 3.2 Для двухопорной балки с консолью, работающей на изгиб, требуется:

1. определить величины опорных реакций; выполнить проверку правильности определения данных реакций;

2. определить величины поперечной силы и изгибающего момента на всех участках балки; построить эпюры соответствующих внутренних силовых факторов;

3. подобрать размеры поперечного сечения стальной балки для случаев: двутавровой; прямоугольного поперечного сечения; круглого поперечного сечения; кольцевого поперечного сечения; выбрать рациональное сечение, в зависимости от соотношения расходов материала на единицу длины балки;

4. вычислить нормальные и касательные напряжения в характерных точках двутаврового сечения балки, построить эпюры соответствующих напряжений;

5. проверить балку двутаврового сечения по 3-й теории прочности.

Дано:

1. допускаемые напряжения для стали: нормальное напряжение ; касательное напряжение ;

2. внешние усилия ; ; ;

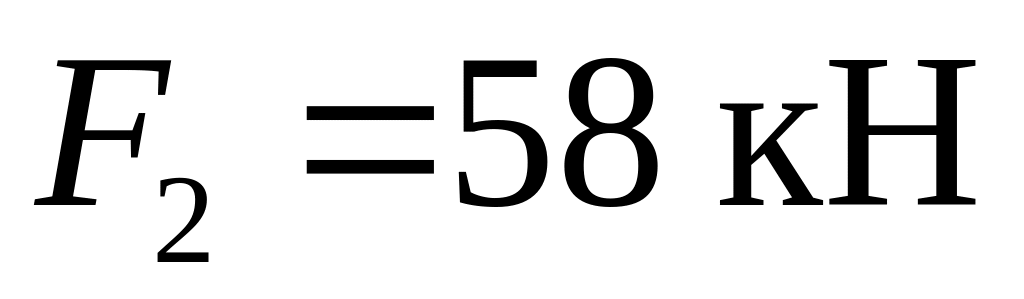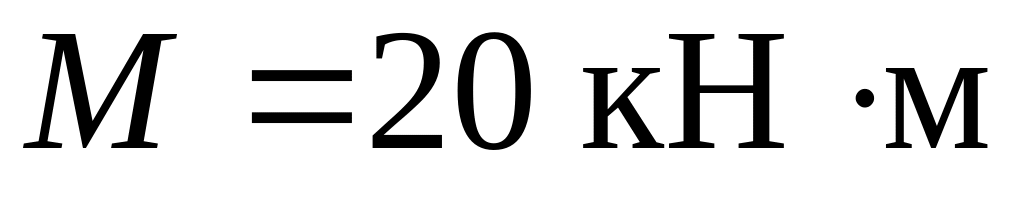3. длины участков ; ; ;

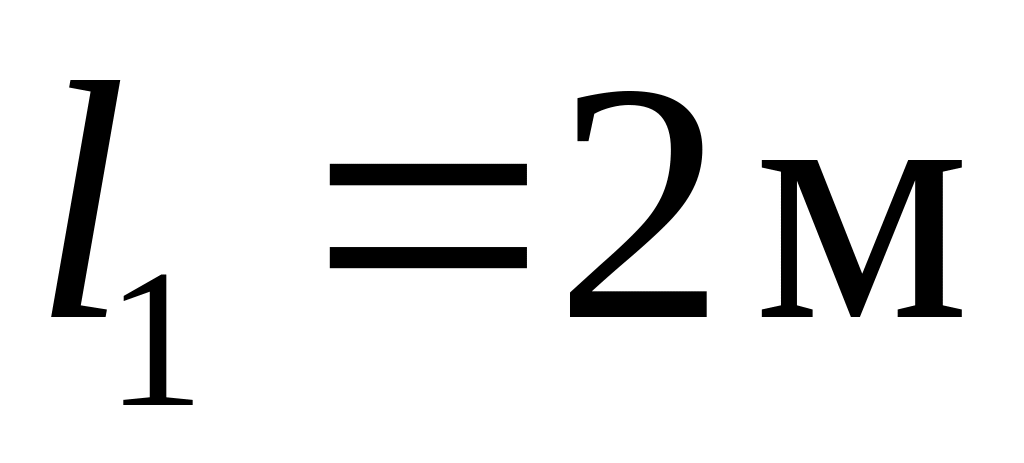4. отношение большей стороны к меньшей прямоугольного сечения взять равным ;

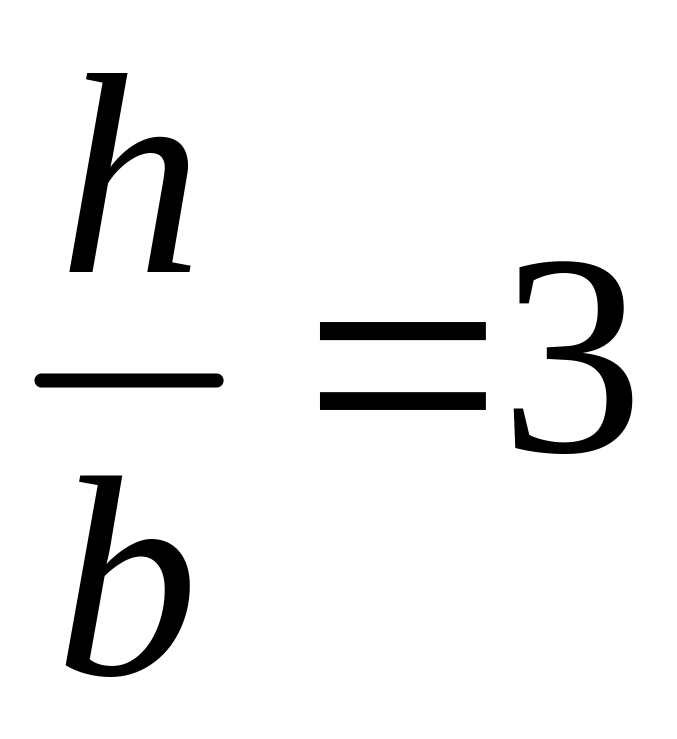5. в кольцевом сечении, соотношение внутреннего диаметра к наружному взять равным .

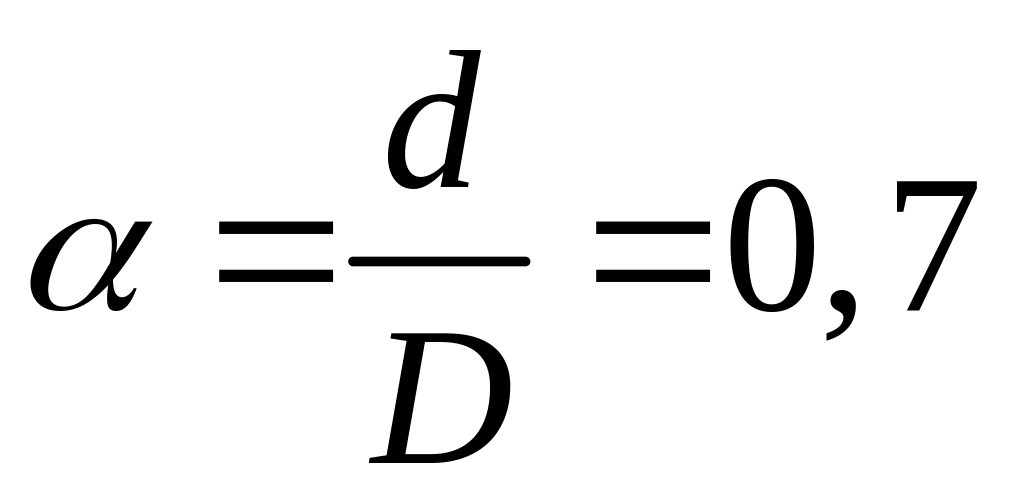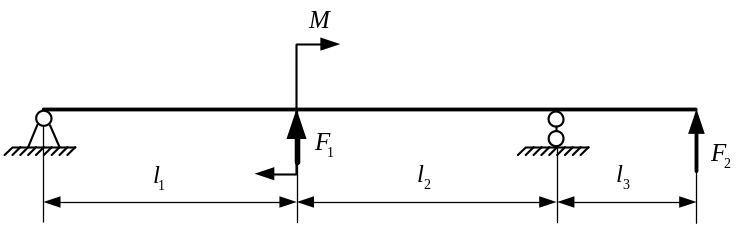
Рис. 3.8. Схема нагружения двухопорной балки с консолью

Решение 1. Заменим действие опор на балку реактивными силами. Действие левой шарнирно-неподвижной опоры  реакцией , а правой шарнирно-подвижной опоры  реакцией (рис. 3.12). Для определения опорных реакций воспользуемся уравнениями равновесия .

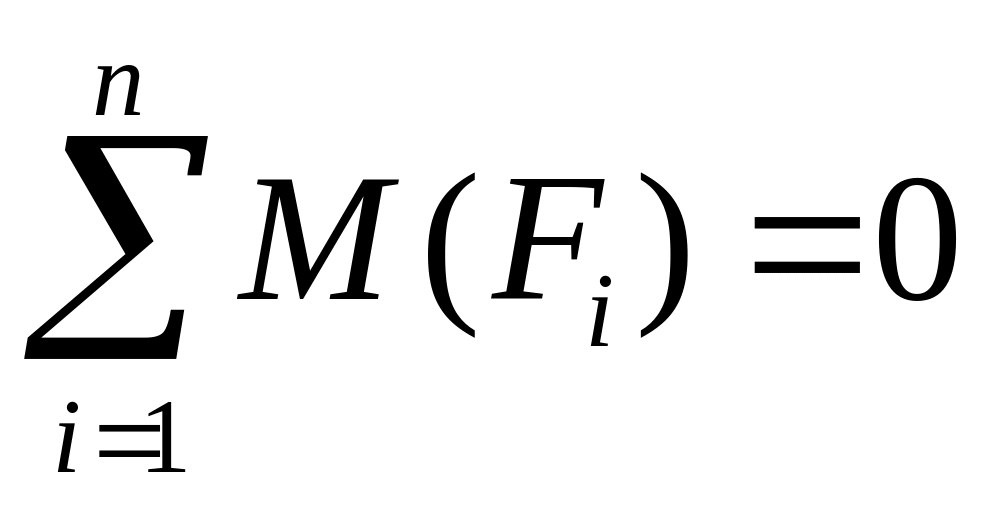Распишем уравнение равновесия 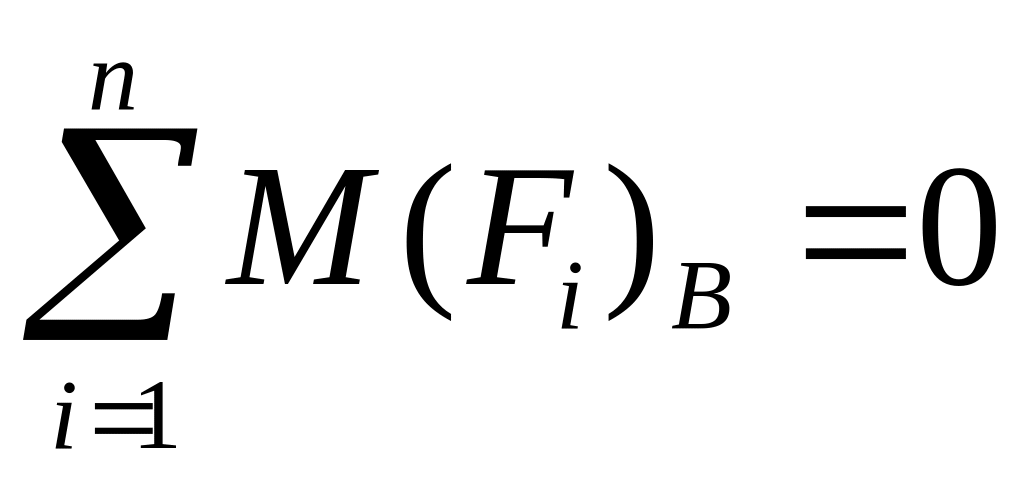для определения реакции в левой опоре:

.

Выразим величину из данного уравнения:

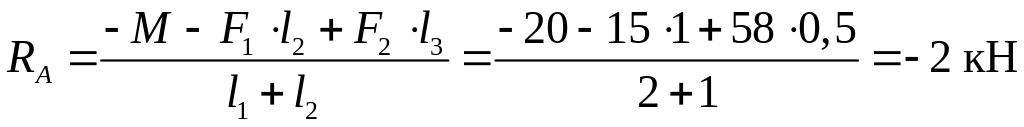
Знак минус у полученной величины реакции означает, что она направлена в противоположную сторону.

Распишем уравнение равновесия для определения реакции в правой опоре:

.

Выразим величину из данного уравнения:

.

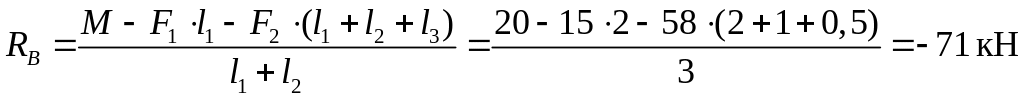Знак минус у полученной величины реакции означает, что она направлена в противоположную сторону.

Перенаправим и в действительные стороны (рис. 3.12)

Выполним проверку правильности определения реактивных сил по уравнению равновесия , получим:

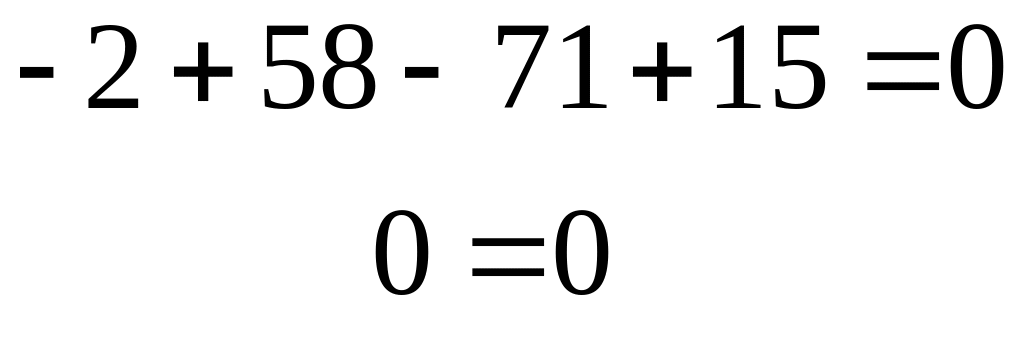
Проверка выполняется, значит опорные реакции найдены верно.

2. Для определения величин поперечной силы и изгибающего момента выполним сечения (рис. 3.12) на участках балки. При этом, первое сечение обязательно должно быть на консольном участке со свободного её конца в сторону опоры.

Рассмотрим первое сечение I-I (рис. 3.9). Его длина изменяется в пределе .

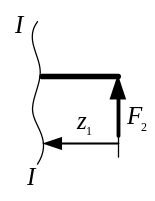
Рис. 3.9. Первый отсечённый участок

Поперечная сила определится по формуле:

.

Изгибающий момент будет равен:

.

Уравнение является уравнением первой степени, так как включает в себя переменную в первой степени. Определим величину момента на границах участка:

при

при .

Рассмотрим второе сечение II-II (рис. 3.10). Его длина изменяется в пределе .

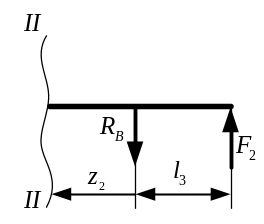
Рис. 3.10. Второй отсечённый участок

Поперечная сила определится по формуле:

.

Изгибающий момент на втором участке определится по уравнению:

.

Уравнение является уравнением первой степени, поэтому изгибающий момент на втором участке будет изменяться линейно. Определим его величину на границах участка:

при

при .

Рассмотрим третий участок III-III (рис. 3.11). Его длина изменяется в пределе .

Поперечная сила определится по формуле:

.

Изгибающий момент на третьем участке определится по следующему уравнению:

.

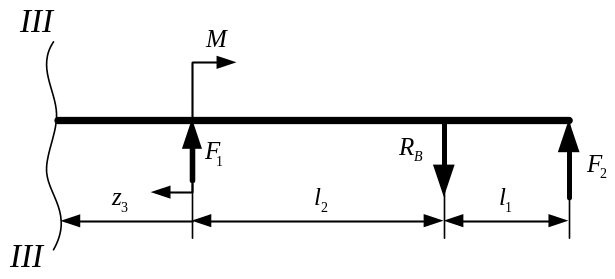
Рис. 3.11. Третий отсечённый участок

Уравнение является уравнением первой степени, поэтому изгибающий момент на третьем участке будет изменяться линейно. Определим его величину на границах данного участка:

при ;

при

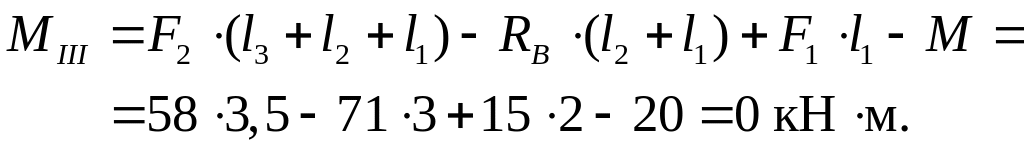
По найденным величинам поперечной силы и изгибающего момента на участках балки, строим соответствующие эпюры (рис. 3.12) в выбранном масштабе.

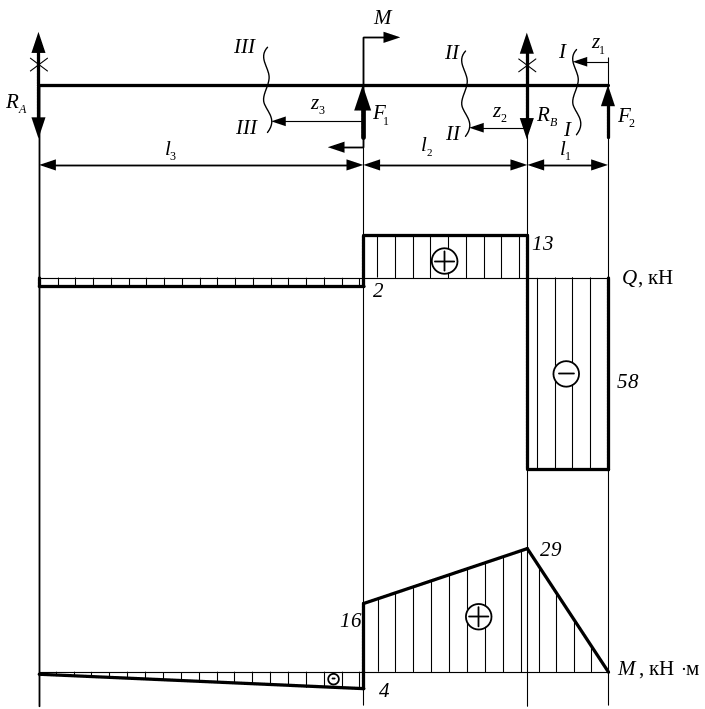
Рис. 3.12. Схема нагружения пространственной балки с эпюрами

3. Для определения размеров поперечного сечения балки различных профилей, преобразуем условием прочности при изгибе (3.1) и выразим момент сопротивления сечения

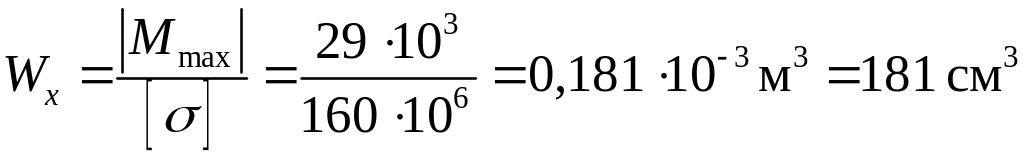
По найденной величине подберём двутавровое сечение балки (ГОСТ 8239-89). Ближайшее значение соответствует двутавру №20, с площадью поперечного сечения .

Выразим из формулы (3.2) диаметр круглого поперечного сечения, получим:

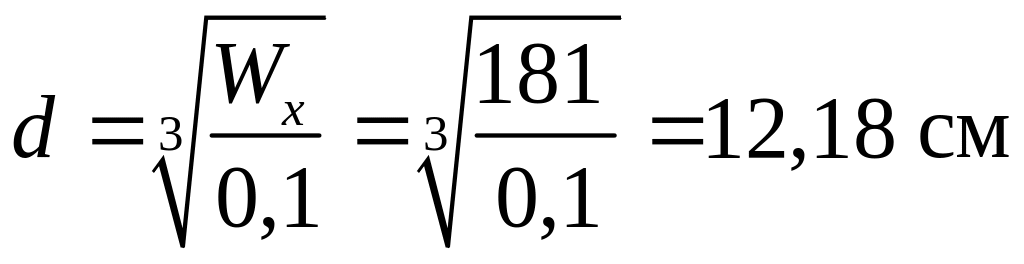
Соответственно, площадь сечения будет равна:

.

Наружный диаметр кольцевого сечения определится по формуле:

.

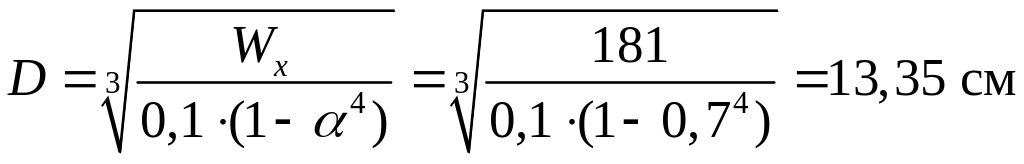Внутренний диаметр кольцевого сечения будет равен:

.

Зная величины наружного и внутреннего диаметров, определим площадь сечения:

Зная величину соотношения сторон сечения ( ) выразим из формулы (3.3) ширину прямоугольника :

.

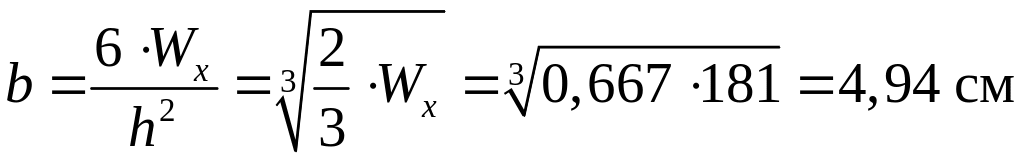Высота прямоугольника равна:

.

Зная геометрические параметры прямоугольного сечения, определим его площадь:

.

Наиболее рациональным сечением в зависимости от соотношения расходов материала на единицу длины балки будет являться сечение с минимальной площадью. Сравнивая значения площадей рассматриваемых сечений, получаем, что наиболее рациональным является двутавровое ( ). Данное утверждение наглядно доказывается соотношением площадей. Приняв площадь двутавра за единицу площади, получаем следующие соотношения:

.

Наиболее нерациональным является круглое поперечное сечение.

4. Запишем геометрические характеристики выбранного нами двутавра №20:

высота двутавра ; ширина полки ; толщина стенки ; средняя толщина полки ; площадь поперечного сечения  ; момент инерции ; моменты сопротивления , ; статический момент полусечения  ; радиус инерции .

Расчёт нормальных и касательных напряжений будем проводить для сечений балки, в которых имеется максимальные значения изгибающего момента и поперечной силы. В нашем случае ; .

Обозначим характерные точки по высоте двутаврового сечения, для которых будем определять величины напряжений (рис. 3.13).

В точке 1 ( ) нормальное напряжение будет равно:

.

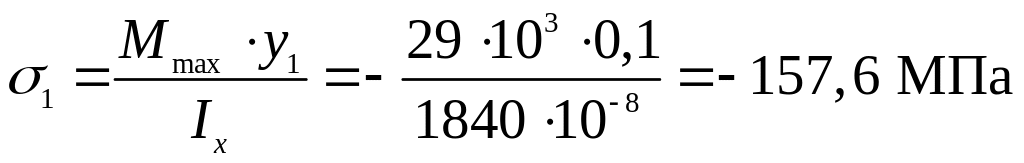Так как изгибающий момент в опасном сечении имеет положительный знак, то точки 1 и 2 лежат в сжатой зоне, следовательно, напряжение в данных точках отрицательно.

Для точки 2 расстояние равно:

.

Определим величину напряжения в точке 2:

.

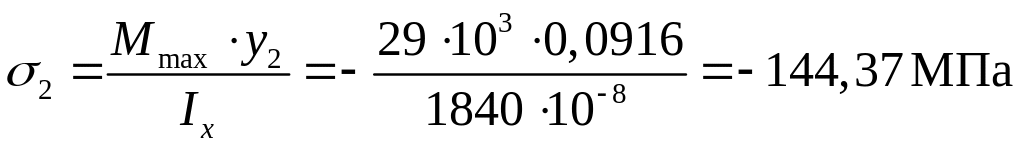Точка 3 лежит на нейтральной оси, поэтому расстояние , следовательно, нормальное напряжение тоже равно нулю ( ).

Точки 4 и 5 лежат в растянутой зоне сечения, поэтому напряжения в данных точках будет положительное, а их величины будут теми же самыми, что и в точках 2 и 1:

для точки 4 ;

для точки 5 .

Величина касательных напряжений в двутавровом сечении изменяется скачкообразно, так как ширина волокна переменна. А резкое изменение ширины сечения вызывает местное распределение напряжений.

Знак касательных напряжений совпадают со знаком поперечной силы.

В точках 1 и 5 статический момент равен нулю, так как нет площади отсечённой части. Следовательно, и напряжения в данных точках будут равняться нулю, т. е. .

Для точек 2 и 4 отсечённые ими площади сечения одинаковы. Статический момент для них будет равен:

.

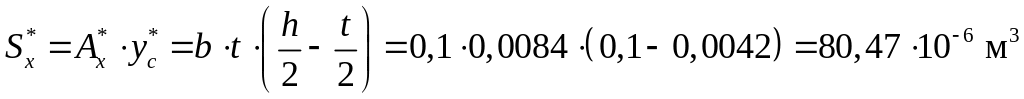Зная величину определим значения касательных напряжений:

при ;

при .

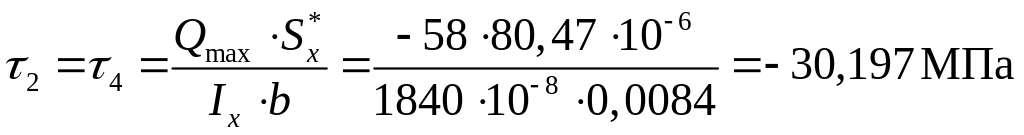В точке 3 значение статического момента берётся из справочника , а ширина поперечного сечения принимается . Тогда касательное напряжение в этой точке будет равно:

.

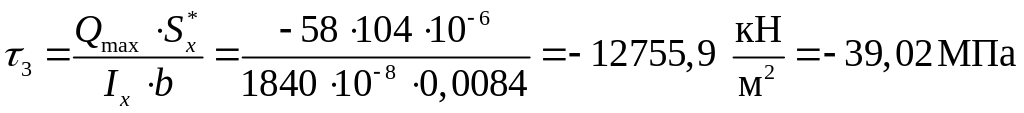По найденным величинам нормальных и касательных напряжений строим эпюры и (рис. 3.6).

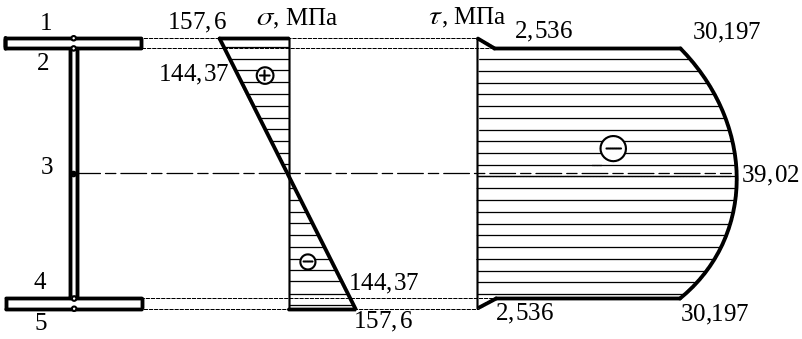
Рис. 3.13. Эпюры напряжений.

Анализируя эпюры видно, что максимальное касательное напряжение имеет место на нейтральной линии ( ), максимальное нормальное напряжение  на границах двутаврового сечения ( ), т. е. в точках 1 и 5.

5. Проверим балку двутаврового сечения по условию прочности при изгибе по касательным напряжениям (3.4).

Для стальных балок по 3-й теории прочности допускаемое касательное напряжение будет равно:

.

В нашем случае, для балки двутаврового сечения будем иметь:

Следовательно, условие прочности выполняется.

Задание 3.2 Для двухопорной балки с консолью, работающей на изгиб, требуется:

1. определить величины опорных реакций; выполнить проверку правильности определения данных реакций;

2. определить величины поперечной силы и изгибающего момента на всех участках балки; построить эпюры соответствующих внутренних силовых факторов;

3. подобрать размеры поперечного сечения стальной балки для случаев: двутавровой; прямоугольного поперечного сечения; круглого поперечного сечения; кольцевого поперечного сечения; выбрать рациональное сечение, в зависимости от соотношения расходов материала на единицу длины балки;

4. выполнить чертежи всех вариантов поперечного сечения балки;

5. вычислить нормальные и касательные напряжения в характерных точках двутаврового сечения балки, построить эпюры соответствующих напряжений;

6. проверить балку двутаврового сечения по 3-й теории прочности.

Допускаемые напряжения для стали взять равными: нормальное напряжение ; касательное напряжение .

Схемы нагружения двухопорной балки представлены на рис. 3.14, исходные данные к схемам указаны в таблице 3.1.

Таблица 3.1

Номер варианта
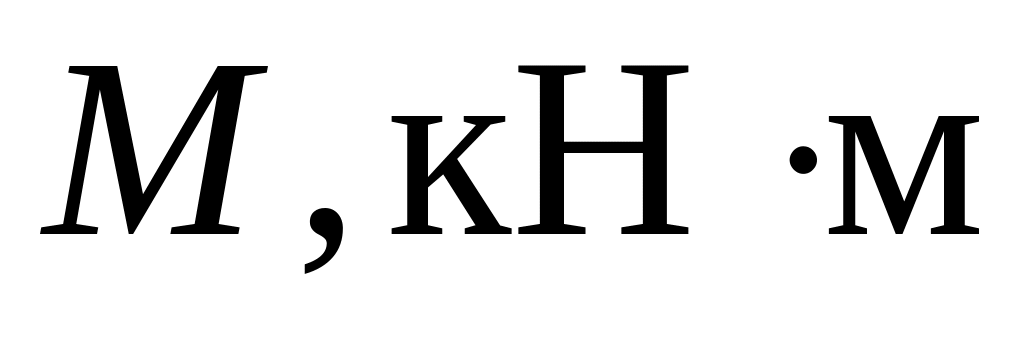
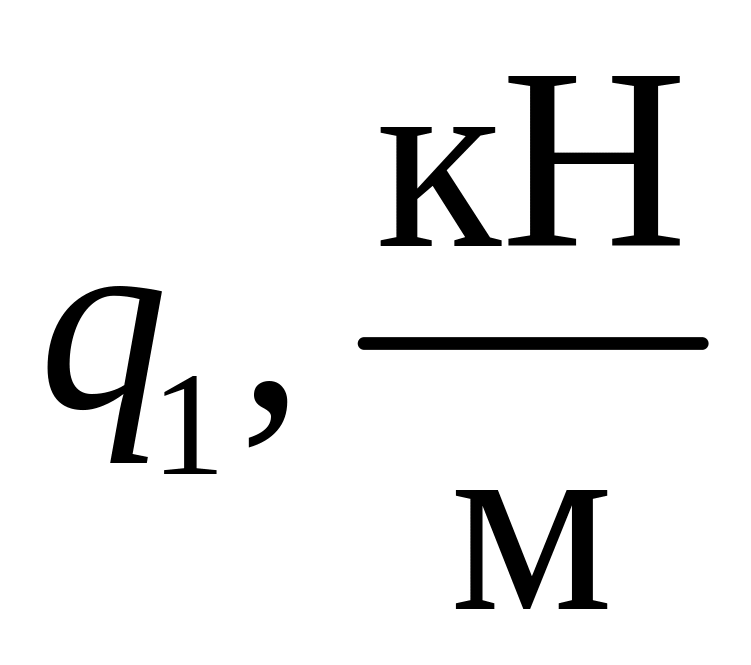
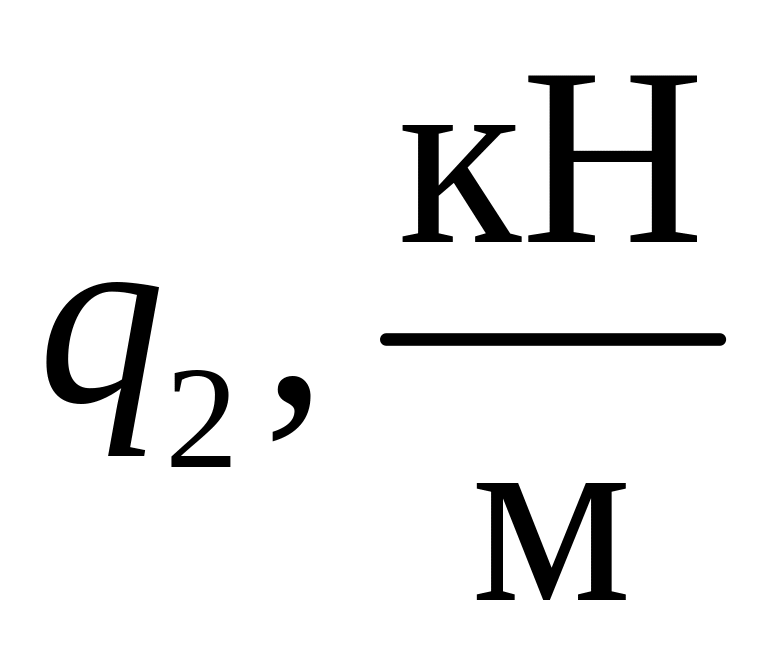
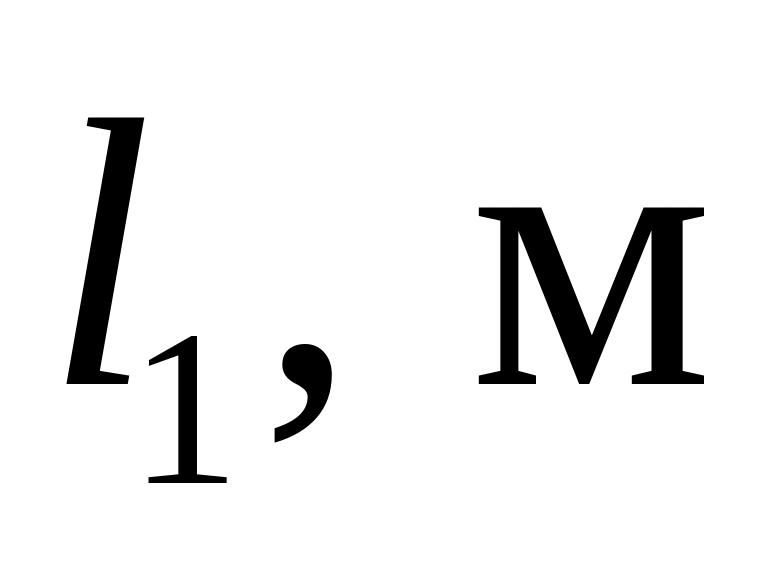
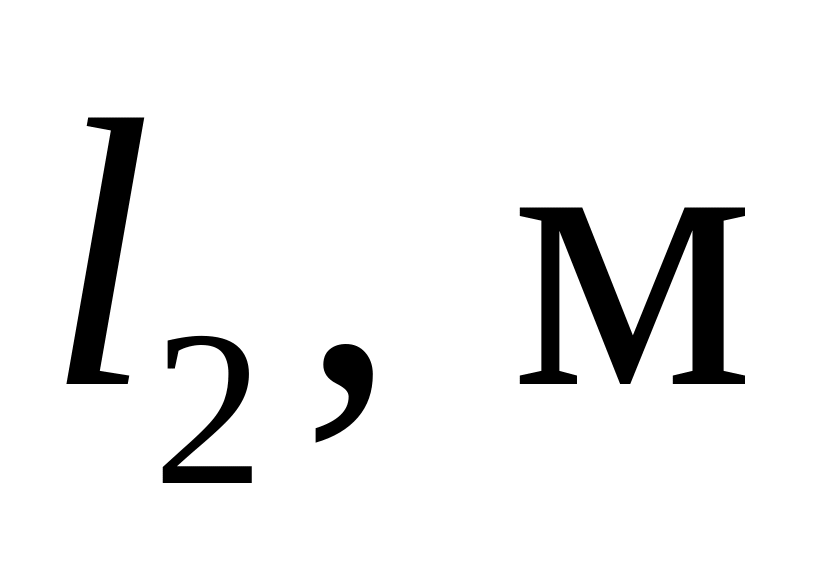
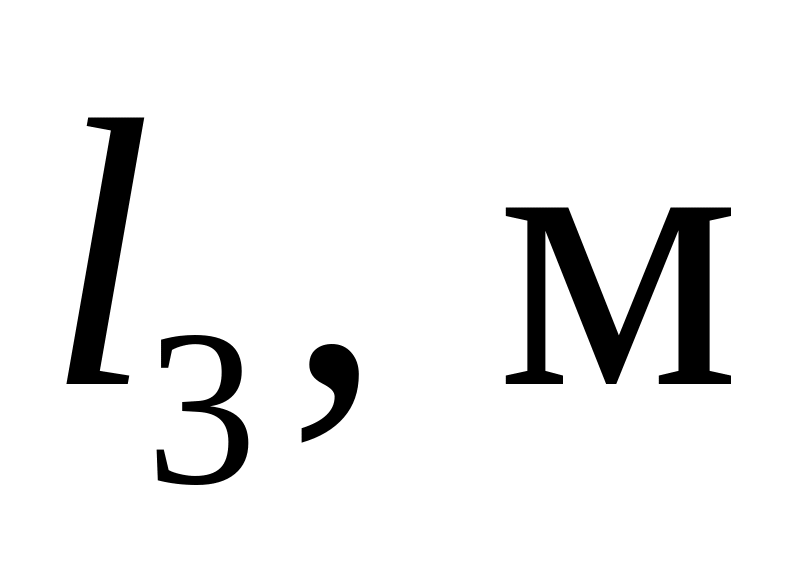
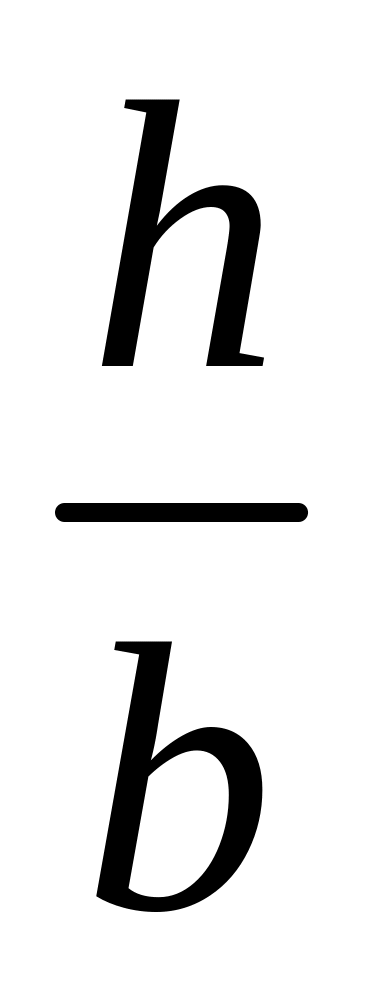
1	30	50	20	40	20	1,1	0,5	2	2	0,6
2	45	35	25	55	15	1,4	2	1,5	3	0,8
3	50	25	40	20	10	1	0,8	1,7	4	0,9
4	25	54	55	15	15	2	1,3	1,6	5	0,7
5	30	40	60	20	30	1,4	0,6	0,5	3	0,75
6	35	42	45	20	10	0,6	1,3	1,5	2	0,65
7	25	20	50	15	25	0,8	2	1,2	4	0,85
8	35	15	45	10	20	1	1,5	2	3	0,7
9	80	100	40	150	200	2	1,5	1	5	0,8
10	55	35	45	60	75	1,3	0,7	1,5	5	0,9
11	30	20	25	35	40	2	1,8	0,8	4	0,6
12	15	30	45	25	16	0,8	1,4	1,5	3	0,85
13	44	34	24	12	12	1,8	1,2	2	2	0,85
14	58	26	48	88	96	1,4	0,5	1	4	0,75
15	22	28	45	6	15	1,3	0,4	0,8	3	0,8
16	30	40	55	85	90	1,2	2,2	0,9	5	0,65
17	40	75	50	30	40	0,6	1	2	3	0,75
18	50	20	60	100	15	1,5	0,7	1,4	4	0,85
19	60	45	15	60	55	2	1	0,5	2	0,65
20	35	50	15	30	25	1,5	0,5	0,5	2	0,9

Рис. 3.14

Рис. 3.15

Рис. 3.16