1.4. Типові алгоритми бцу

На базі ЗОТ можливо реалізувати складні та ефективні закони управління та регулювання. При побудові алгоритмів управління технологічними процесами на базі ЗОТ виходять з принципів дії добре досліджених пропорційного (П), інтегрального (І), пропорційно-інтегрального (ПІ), пропорційно-інтегрально-диференційного (ПІД) регуляторів.

Закон управління аналогового ПІД-регулятора можна представити рівнянням:

(1.6)

де - управляючий вплив;

e(t) - відхилення регулюючої величини від завдання регулятора;

К_р - коефіцієнт підсилення;

Т_Д - постійна часу диференціювання;

Т_і - постійна часу інтегрування.

Замінимо неперервні функції , e(t) решітчатими функціями:

(1.7)

Для представлення дискретних ПІД законів управління застосовують такі алгоритми.

Позиційний алгоритм оснований на розрахунку повної величини управляючого впливу:

(1.8)

де .

Розглянемо алгоритм роботи цифрового ПІД-регулятора, проаналізувавши кожну з його складових окремо.

Пропорційна складова на n-му періоді квантування може розглядатись автономно в алгоритмі позиційного управління:

(1.10)

22

Інтегральна складова в позиційному алгоритмі, виходячи з трапецеїдального правила для числового інтегрування:

(1.11)

Застосовуючи інший спосіб представлення інтегральної складової:

(1.12)

Сигнал на виході ідеальної диференційної ланки для позиційного алгоритму в дискретній формі має вигляд:

(1.13)

Згідно вищезгаданого управляючий вплив при позиційному алгоритмі приймає вигляд:

(1.13)

Віднімемо з обох частин рівняння (1.13.) величину U_n-1 в результаті чого отримаємо:

(1.14)

яке можна перетворити до вигляду:

Після введення позначень:

, (1.16)

, (1.17)

, (1.18)

23

Основне рівняння позиційного регулювання має вигляд:

(1.19)

яке наведено в формі зручній для програмування. Оцінка коефіцієнтів А₀, А₁, А₂ еквівалентна оцінці величин k_p, T_i, T_Д при постійному T₀.

На підставі отриманих виразів для конкретних умов праці розраховується повна величина управляючого впливу на заданому T₀ і

передається на ЦАП і далі на виконуючий пристрій.

Швидкісний алгоритм відрізняється тим, що вихідний сигнал являє собою похідну або швидкість дії управляючого впливу, і є наслідком диференціювання позиційного алгоритму і реалізується за допомогою спільної роботи цифрового регулятора та виконавчого механізму. Інтегрування здійснюється виконавчим механізмом (наприклад, інтегральним операційним підсилювачем з цифровим виходом). В цьому випадку не потрібний спеціальний ЦАП.

При швидкісному алгоритмі на кожному періоді квантування визначається приріст управляючого впливу.

(1.20)

Аналогічно позиційному алгоритму пропорційна складова управляючого впливу має вигляд:

(1.21)

На основі рівняння (1.11) знаходимо вираз для приросту інтегральної складової:

(1.22)

Сигнал на виході інтегральної диференційної ланки для швидкісного алгоритму на основі виразу (1.13) отримаємо в слідуючому вигляді:

(1.23)

Для цифрових систем характерна постійність завдання впливу регулятора G=const на певному проміжку часу. Приймаючи до

24

уваги е_п =G_n -Y_n, надамо швидкісний алгоритм в слідуючому виді:

(1.24)

з якого видно, що завдання впливу регулятора G присутнє тільки в прирості інтегральної складової. Якщо інтегральну складову виключити, то неможливо запобігти дрейфові регулятора.

В реальних умовах в наслідок дії завад диференційна складова управляючого впливу на виході системи приймає більше значення за рахунок скачкоподібних приростів похибки неузгоджненості е_n = G_n -Y_n.

Для зменшення впливу високочастотних завад застосовуються різні способи фільтрації диференційної складової.

Першим способом фільтрації є застосування реальної диференційної ланки з постійною часу T_ф = (10-100)T₀. Сигнал на виході такої ланки в аналоговій формі можна надати у вигляді:

(1.25)

В дискретній формі при позиційному алгоритмі він прийме вид:

(1.26)

а при швидкісному алгоритмі:

(1.27)

Крім введення постійної часу фільтра для зменшення впливу завад розроблено інший спосіб диференціювання в дискретній формі по чотирьом точкам. Нехай середня величина вихідної змінної, що регулюється, за чотири опитування дорівнює:

(1.28)

Тоді,

25

. (1.29)

Вплив завад знижується шляхом опосередкування змінної, що управляється, у при обчислені диференційної складової в дискретній формі на основі врахування передісторії вимірювань у.

Беручи до уваги (1.29.), швидкісний алгоритм управління надамо у вигляді:

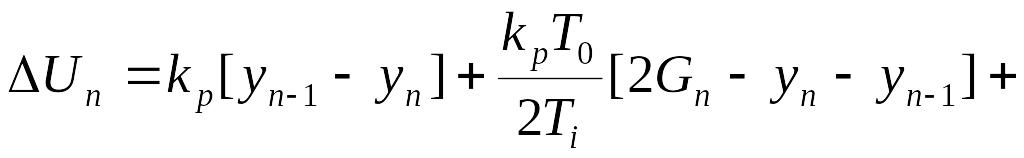
(1.30)

Питання для самоконтролю

1. Які існують категорії систем управління?

2. Які апаратні засоби складають систему управління?

3. Функції та варіації структури підсистеми аналогового введення.