4. Синтез систем логічного управління

Серед різновиду систем управління важливе місце займають системи логічного управління (СЛУ). Характерним признаком цих систем є застосування двійкових датчиків та виконавчих механізмів у вигляді джерел вхідних і приймачів вихідних сигналів. При проектуванні СЛУ широко використовуються типові СІС та БІС, що дозволяють реалізувати апаратним (схемотехнічним) шляхом складні функції й алгоритми. До числа таких СІС відносяться арифметико-логічні, регістрові, рахувальні та тригерні пристрої, суматори множники, мультиплексори, шифратори, компаратори та ін. Менш відомі в практиці проектування такі СІС, як мультиплексори (MX), щo являють собою логічний пристрій, що містить g-управляючих входів U₁, U₂, ..., U_g; 2^g інформаційних входів D0, D1, ..., D2^g-1, стробуючий вхід та вихід. При подачі на управляючі входи деякої комбінації двійкових сигналів і відповідного сигналу на вхід стробування до виходу Y мультиплексора підключається той інформаційний вхід, порядковий номер якого відповідає вазі двійкової комбінації управляючих сигналів.

Побудова логічних схем на мультиплексорах проводиться у вигляді структур, що відрізняються способами функціонального розділення і розкладення булевих функцій (БФ). Найбільш часто на практиці застосовується розкладання БФ по способу Шеннона:

де - залишкові функції розкладання, що одержуються із функції шляхом підстановки констант 0 і 1 замість змінних множини

для маємо

для маємо

для _l маємо

Наприклад, булева функція має вид:

97

Для компактності представлення заданої булевої функції використовують десяткову форму запису з позначенням нею окремих термів (кон'юнкцій), представивши її у вигляді множини :

З урахуванням специфіки роботи мультиплексорів і конструктивних особливостей їх реалізації з числом управляючих входів g=2,3,4 та інформаційних входів, рівним 2^g (4,8,16), розкладання заданої БФ можна вести за двома, трьома або чотирма змінними. Тоді при побудові логічної схеми на мультиплексорах змінні повинні підключатись до управляючих входів а залишкові функції (ЗФ) розкладання - до інформаційних входів відповідного MX. Якщо утворені в результаті першого кроку ЗФ мають нетривіальний вид, то процедура розкладання кожної, що одержуємо на черговому кроці залишкові функції, повинна повторюватись до моменту перетворення їх у тривіальні, а саме:

0 (відсутня)

Залишкові функції розкладання Q_t по останнім двом , трьом , чотирьом змінним з булевої функції можуть бути обчислені за формулами:

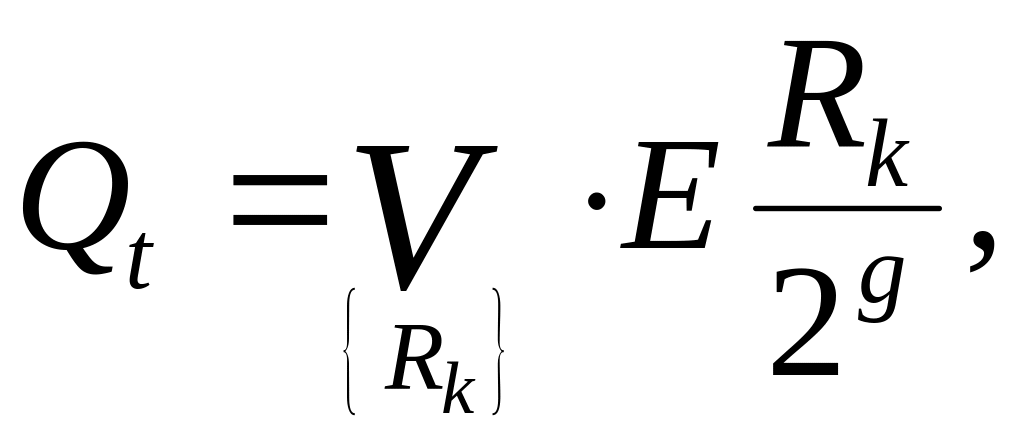
де t=0,1,...,2^g-1;

- ціла частина від ділення ;

- залишок частина від ділення ;

- множина термів БФ;

g - число змінних, по яким розкладається БФ.

98

При побудові логічної схеми на MX, що реалізує задану БФ, можливі два випадки: a) n<=g; б) n>g.

В першому випадку БФ реалізується схемою, що складається з одного мультиплексора, в якому g змінних підключається до управляючих входів MX, а на інформаційні входи подаються константи 0 (якщо данний терм у функції відсутній) або 1 (якщо він присутній).

В другому випадку процес побудови логічної схеми проводиться за результатами розкладання заданої БФ. Внаслідок першого кроку розкладання вихідної БФ по по g змінним одержуємо сукупність ОФ, що залежать вже тільки від n-g змінних. Наступні кроки розкладання зменшують кожний раз число змінних в ЗФ на g, аж до одержання в процесі розкладання ЗФ тривіального виду. Таким чином, число кроків розкладання БФ відповідає числу каскадів схеми на мультиплексорах з підключенням на управляючі входи MX тих змінних, по яких здійснювалось розкладання; на інформаційні входи MX останнього каскаду подаються окремі змінні або , а також сигнали логічного 0 чи логічної 1, виходячи з виду отриманих ЗФ:

Ǿ

Згідно з приведеним вище алгоритмом здійснимо розкладання заданої БФ по двом, трьом та чотирьом змінним, зводячи результати розрахунків у таблиці.

Варіант розкладання БФ по двом змінним наведені у

99

табл.4.1.

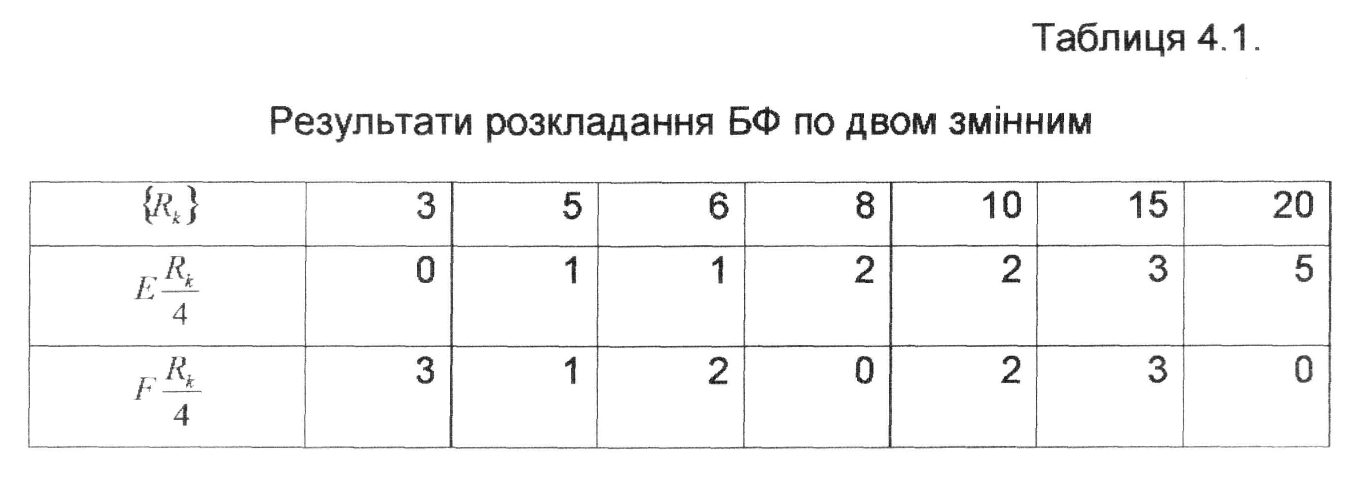
Таким чином, на першому кроці розкладання БФ одержуємо слідуючі ЗФ:

Розкладання БФ продовжимо, так як не всі ЗФ мають тривіальний вид.

На другому кроці у вигляді вихідних даних розглядаються складові кожної з одержаних на першому кроці розкладання залишкові функції Q_t (табл.4.2.).

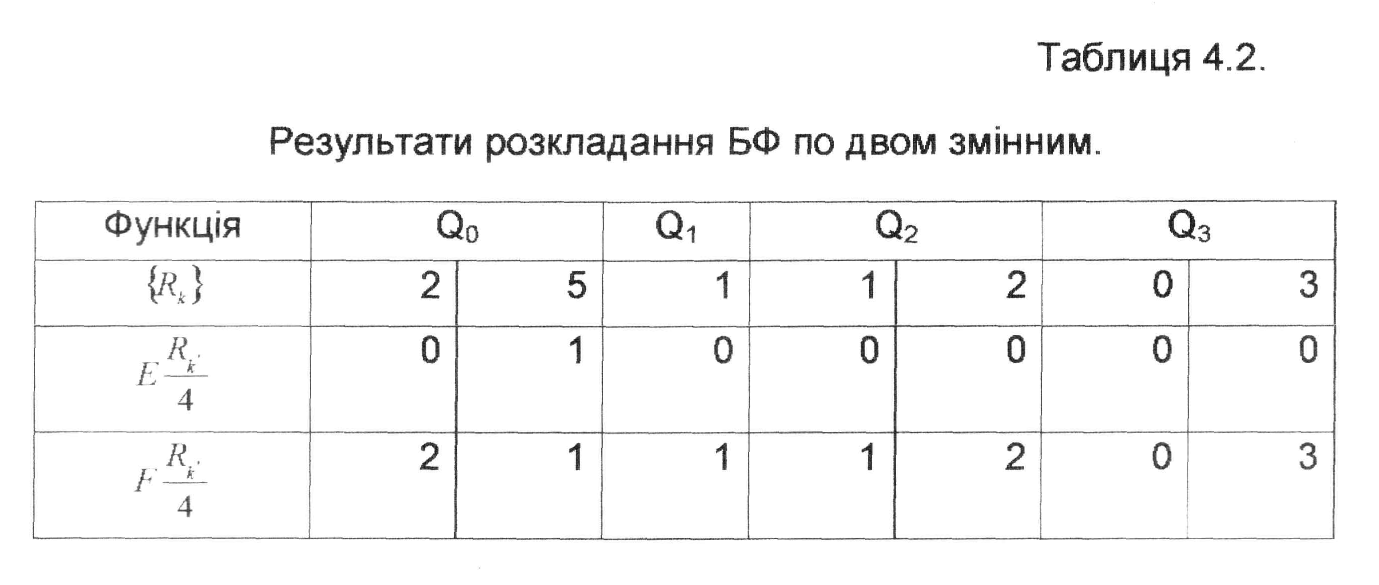
На другому кроці розкладання БФ маємо слідуючи ЗФ:

для Ǿ;

для Ǿ; Ǿ; Ǿ;

для Ǿ; Ǿ;

для Ǿ; Ǿ;

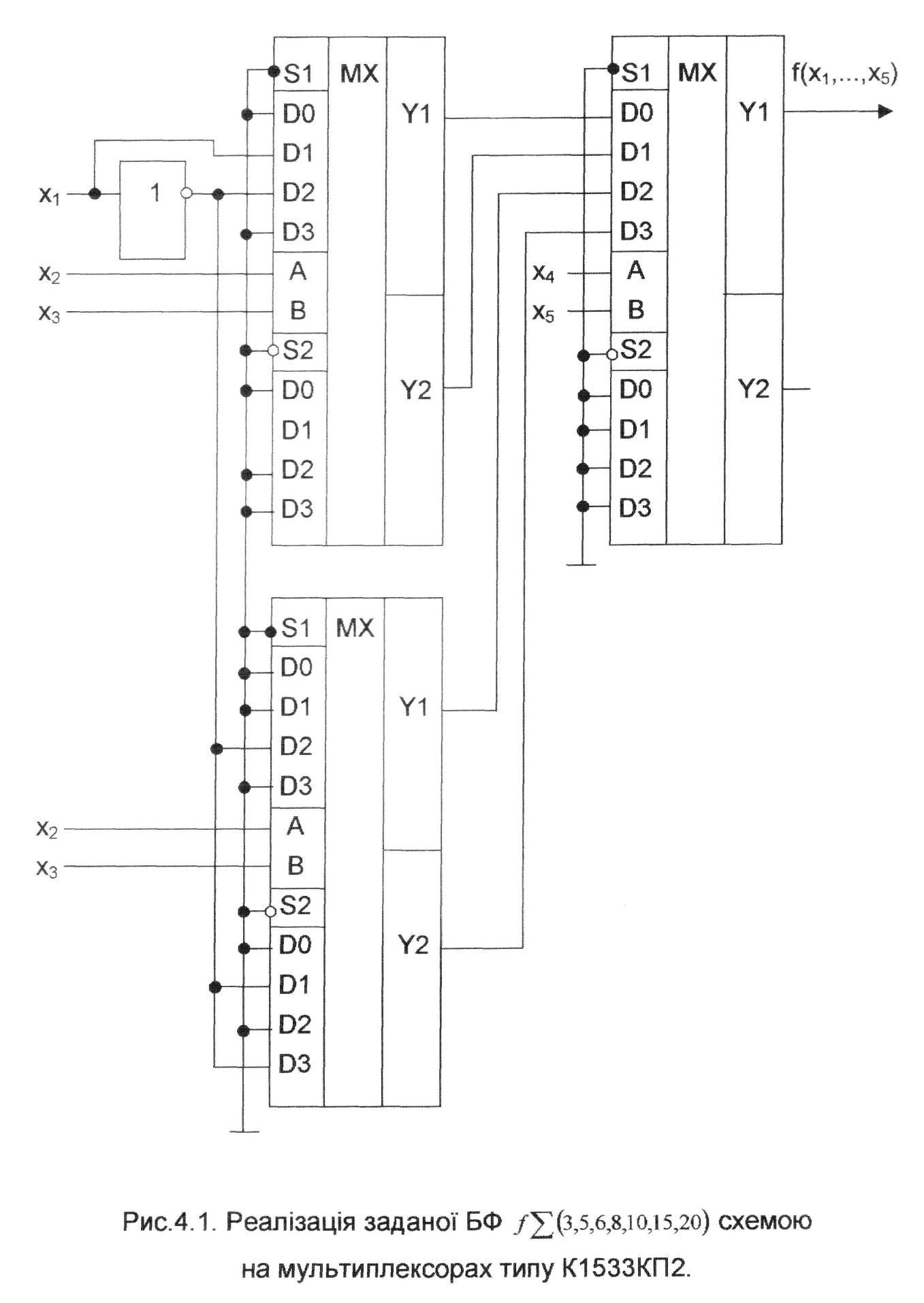
Так як ЗФ, отримані на другому кроці розкладання, є тривіальні, перевіримо до практичної реалізації двокаскадної схеми на MX з g=2. Схемна реалізація БФ на MX типу К1533КП2 наведена на рис.4.1.

Варіант розкладання БФ по трьом змінним наведено в табл.4.3.

100

101

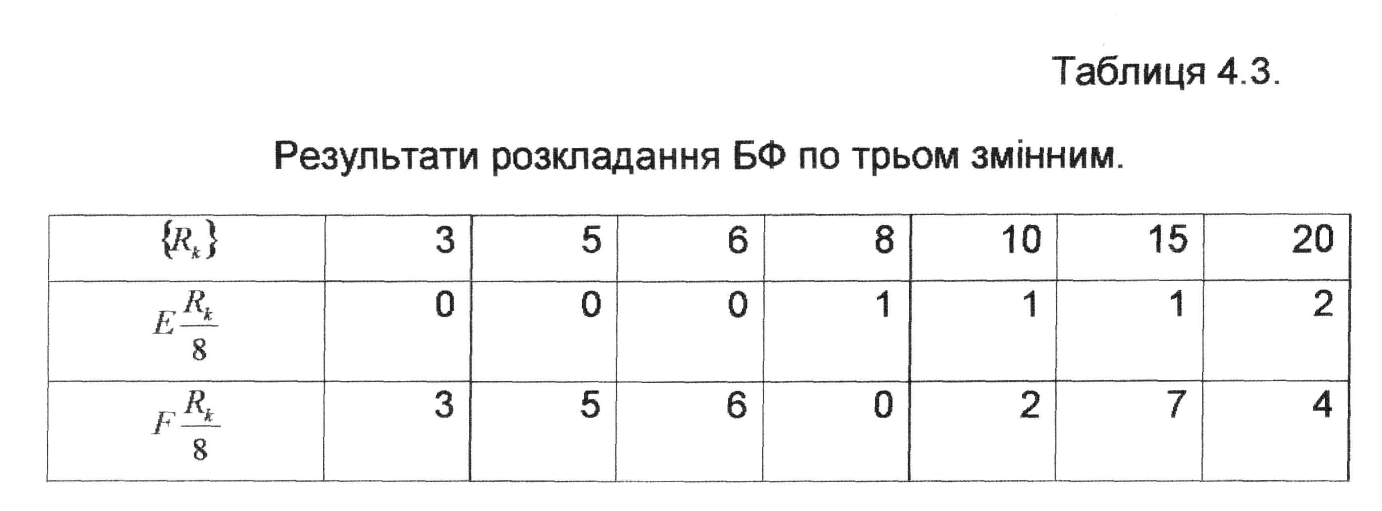
Таким чином, після першого розкладання по трьом змінним отримано наступні ЗФ:

Ǿ;

Оскільки одну частину ЗФ отримали тривіальною (Q₀÷Q₁,Q₅÷Q₇), a іншу (Q₄) - нетривіальною, це свідчить про недоцільність подальшого розкладання БФ та її схемної реалізації (для остаточної реалізації БФ при такому підході потрібно вісім мультиплексорів).

Варіант розкладання БФ по чотирьом змінним наведено в табл.4.4.

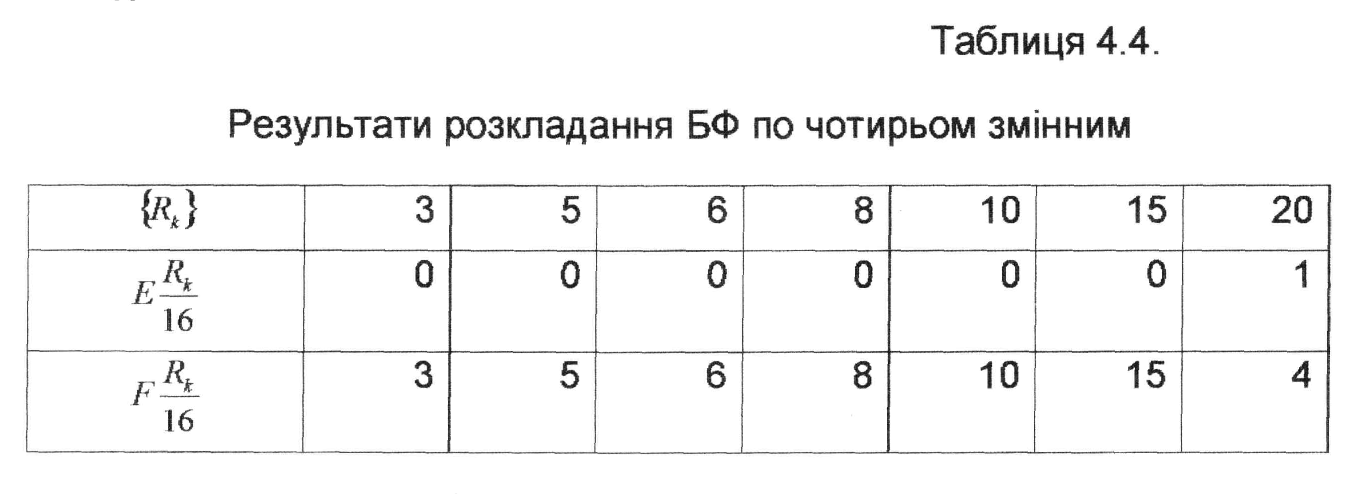
Таким чином, після першого кроку розкладання БФ по чотирьом змінним отримано слідуючі ЗФ:

Q₀=Q₁=Q₂=Q₇=Q₉=Q₁₂=Q₁₃=Q₁₄=Ǿ; Q₃=Q₅=Q₆=Q₈=Q₁₀=Q₁₅= Ǿ;

Q₀=1.

102

103

Оскільки всі ЗФ тривіальні, розкладання БФ закінчуємо і її можна реалізувати на одному MX при g=4. Схемна реалізація заданої БФ на одному мультиплексорі типу К155КП1 наведена на рис.4.2.

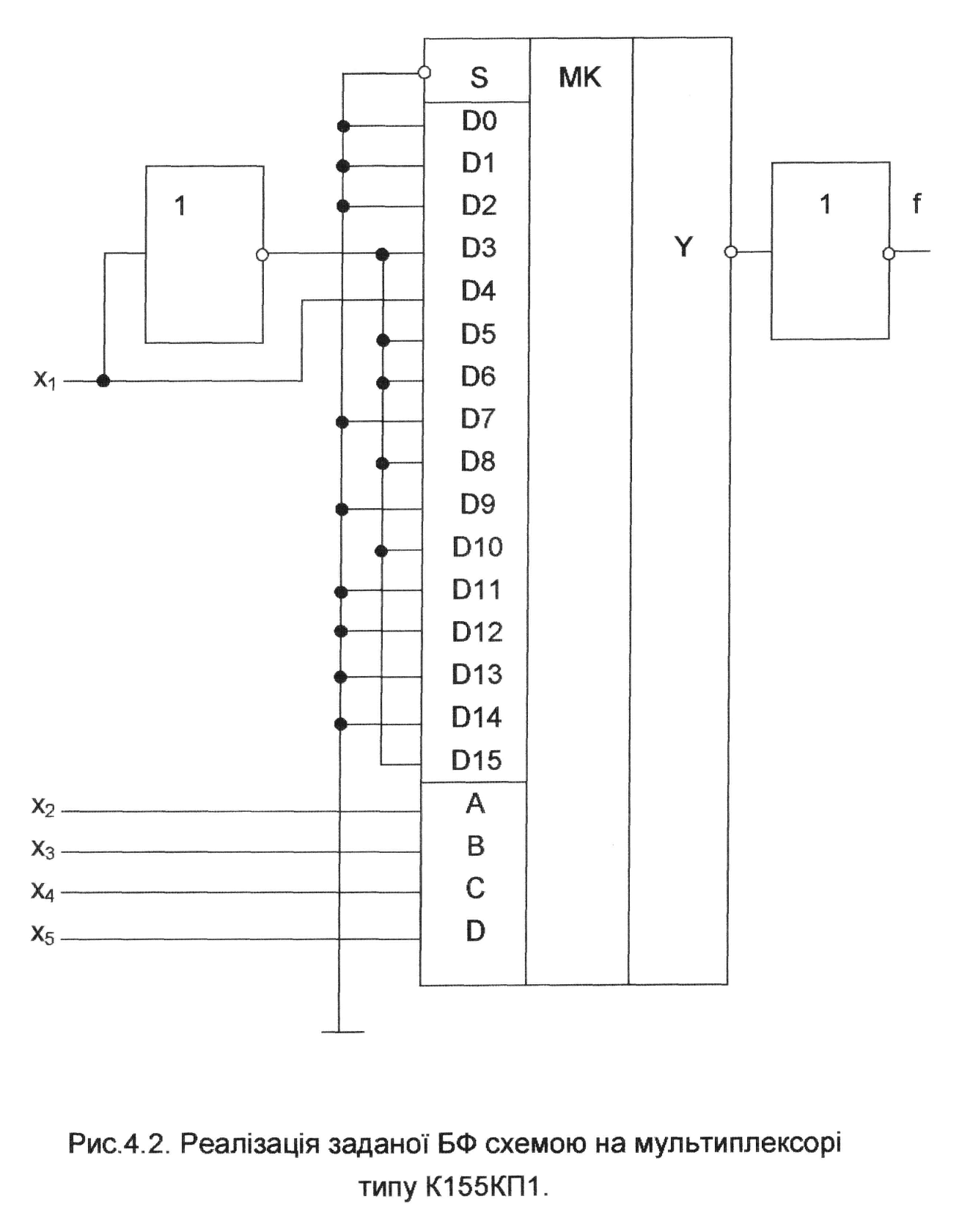
Для реалізації на мультиплексорах краще всього підходять БФ з числом змінних кон'юнкцій до 9.