The information characteristics of sources and channels
The average quantity of information, which gives out a source in unit of time, is named as a source productivity
H =H/ t, bit per second,(bit/sec). (2.5)
For channels of transmitting information there is existing the similar characteristic - speed of information transmitting on the channel. It is possible to consider this speed as average quantity of information, which is transmitting on the channel in unit of time,
R=WH,bitper second, (2.6)
where W is the transmitting speed for electrical code signals;
Н is the average quantity of information, which carries one code signal.
Joint entropy of the message symbols.
The information characteristics of sources of the discrete messages are determined in item 10.1. Their analysis shows, that a source entropy of the discrete messages is its basic information characteristic, through which express the majority others. Therefore it is expedient to consider properties entropy of several next symbols, to show, as the average information quantity for several next symbols is formed, as influence this size non-uniformity of distribution of occurrence probabilities of the messages symbols and static connections between symbols.
Let's consider a syllable from two letters aiai.. If the occurrence of a symbol depends only on what was in the message the previous symbol, formation of syllables from two letters describes by Marcovian simple circuit. Entropy of joint occurrence of two symbols define, applying operation of averaging on all volume of the alphabet:
(2.7)
where
is
probability of formation of a syllable aiai.
as probability of joint occurrence of symbols
and
;
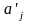Is the information quantity, which is necessary on a syllable.
As
(2.8)
where
,
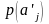- probability of occurrence
;
-
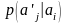probability of occurrence
provided
that before it has appeared
;
-
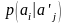probability of occurrence
provided that before it has appeared
,
(10) is possible to present as
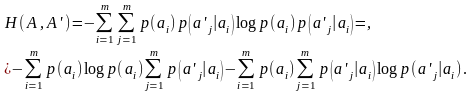
The conditional entropy can be determined through a syllable entropy:
,
(2.9)
.
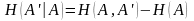(2.10)
The conditional entropy has the following property: if the symbols and also are independent,
The redundancy factor is determined on such formula
.
(2.11)
When H(A/A’) = logm, rs = 0.
Linear Optimum Filtering
Optimal Wiener Filter Design: Example
Signal Generating Model The model is given by the transfer function
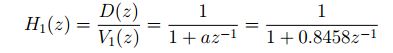
or the difference equation
The channel (perturbation) model is more complex. It involves a low pass filter with a transfer function
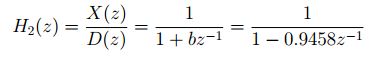
leading for the variable x(n) to the difference equation
and a white noise corruption (x(n) and v2(n) are uncorrelated)
With resulting in the final measurable signal u(n).
FIR Filter The signal u(n) will be filtered in order to recover the original (useful) d(n) signal, using the filter
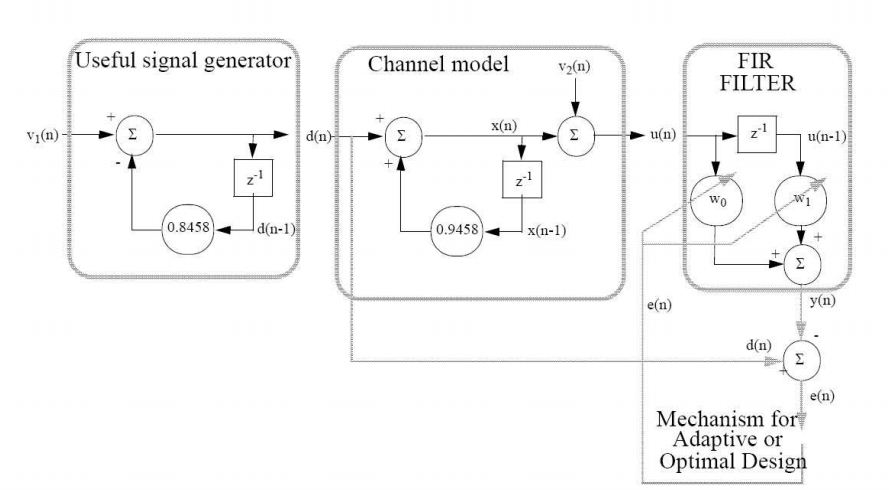
We plan to apply the Wiener - Hopf equations
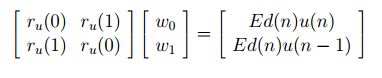
The signal x(n) obeys the generation model
