Процессы управления в автоколебательных системах

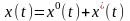
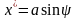
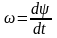(6.29)

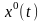—медленная переменная по сравнению с x*(t)

Уравнение динамики системы (рис. 6.1) имеет вид

Q(p)x + R(p)F(x) = S(p)f(t) (6.30)

где f(t) — медленная функция времени (по сравнению с х*).

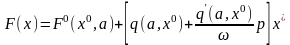(6.31)

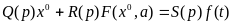(6.32)

Уравнение для периодических составляющих запишется в виде

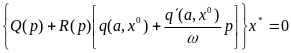(6.33)

(6.34)

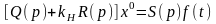(6.35)

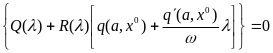
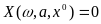
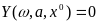(6.37)

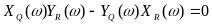, (6.38)

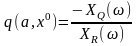(6.39)

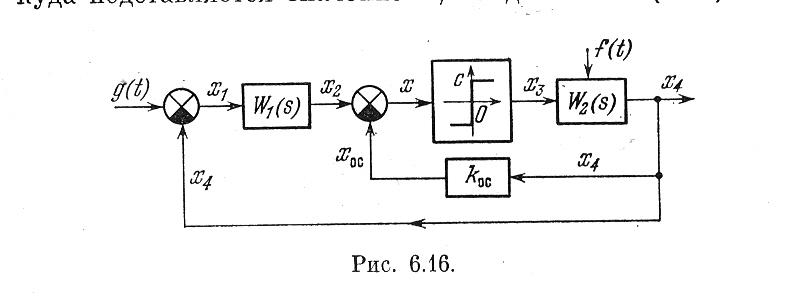
Рис. 6.16.

Колебательные переходные процессы

Уравнение нелинейной системы (рис. 6.20), как известно, имеет вид

Q(p)x + R(p)F(x) = 0 (6.45)

В линейных системах синусоидальные переходные коле­бания имели вид

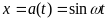
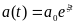(6.46)

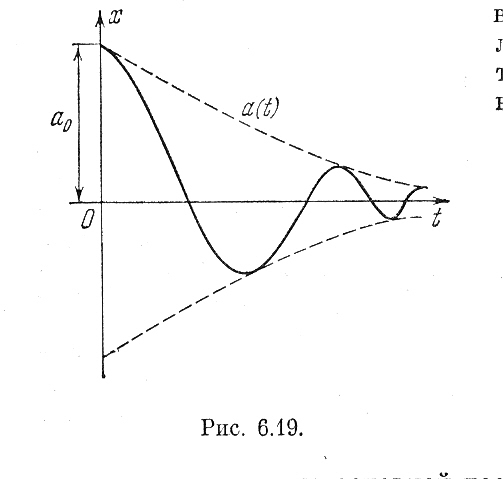
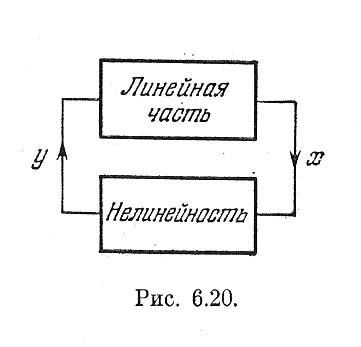
Рис, 6.19. Рис. 6.20.

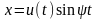
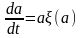
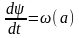(6.47)

X = asinψ, px = αωcosψ + αξsinψ

,

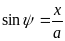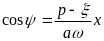
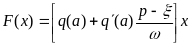
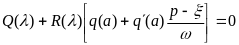(6.48)

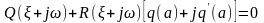(6.49)

X(α, ω, ξ) =0 Y(α, ω, ξ) = 0 (6.51)

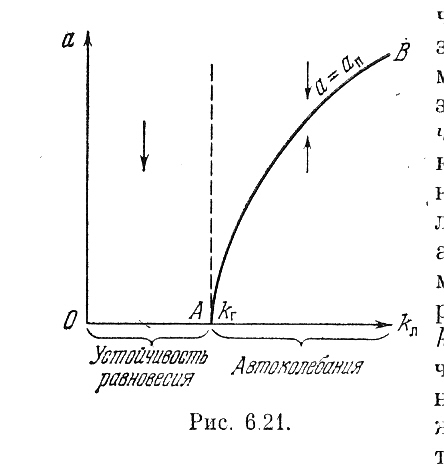
Рис.6.21

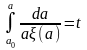(6.52)

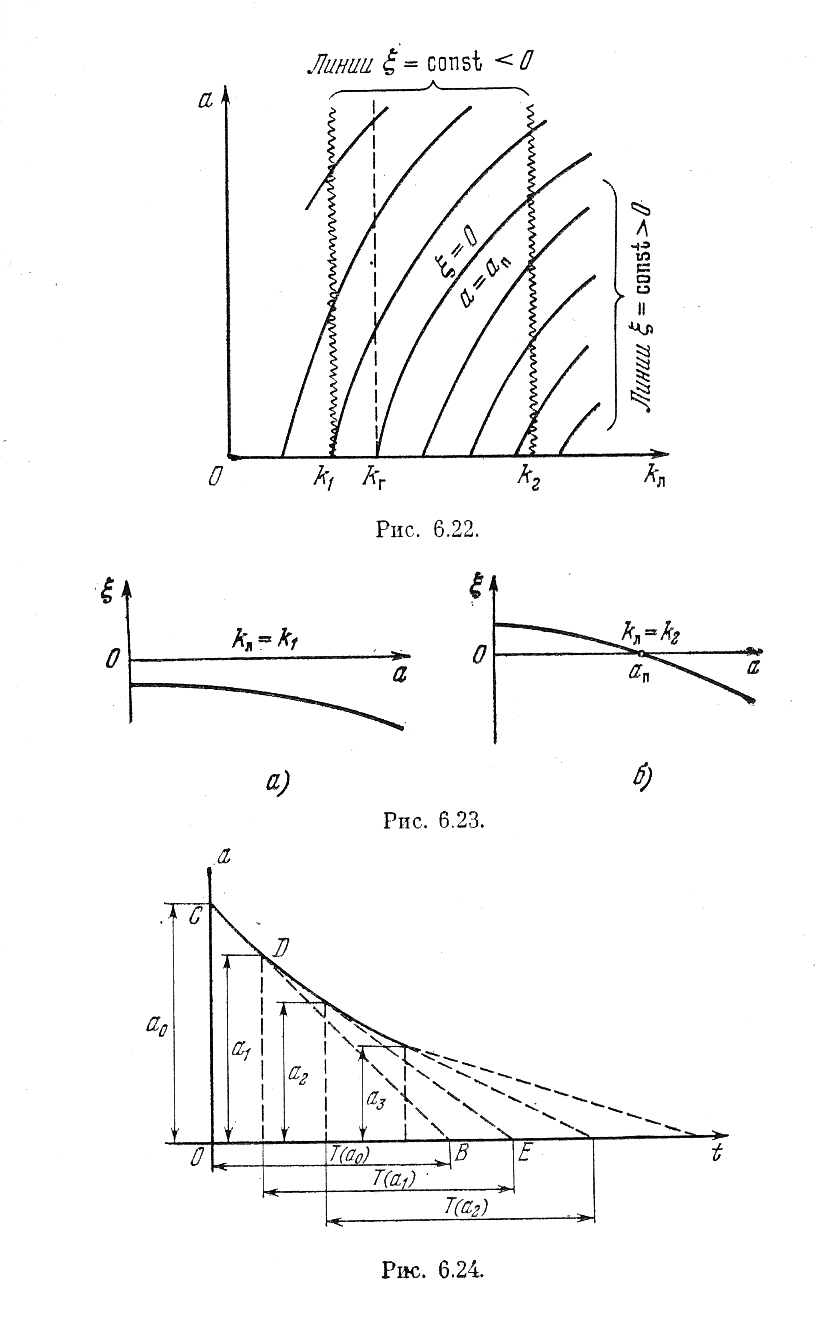
Рис.6.22.

Рис.6.23

Рис.6.24.

Введем в рассмотрение текущую «постоянную времени»

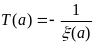(6.53)

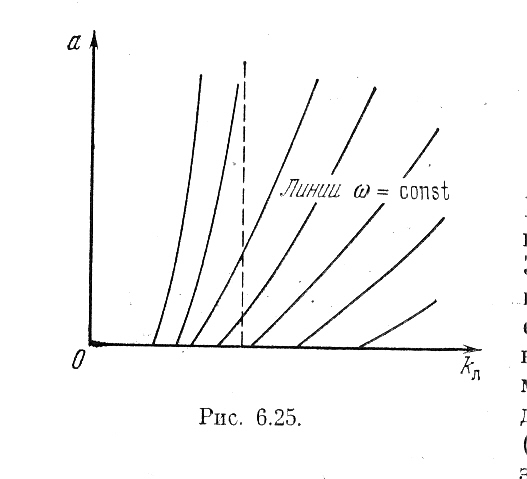
Рис.6.25

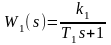
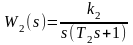
Гармоническая линеаризация нелинейности дает

F(x) = q(α)x

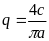
Характеристическое уравнение замкнутой системы в результате получает вид

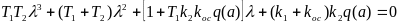
Подставляя в это уравнение λ = ξ +jω, ищем решение в форме (6.47).

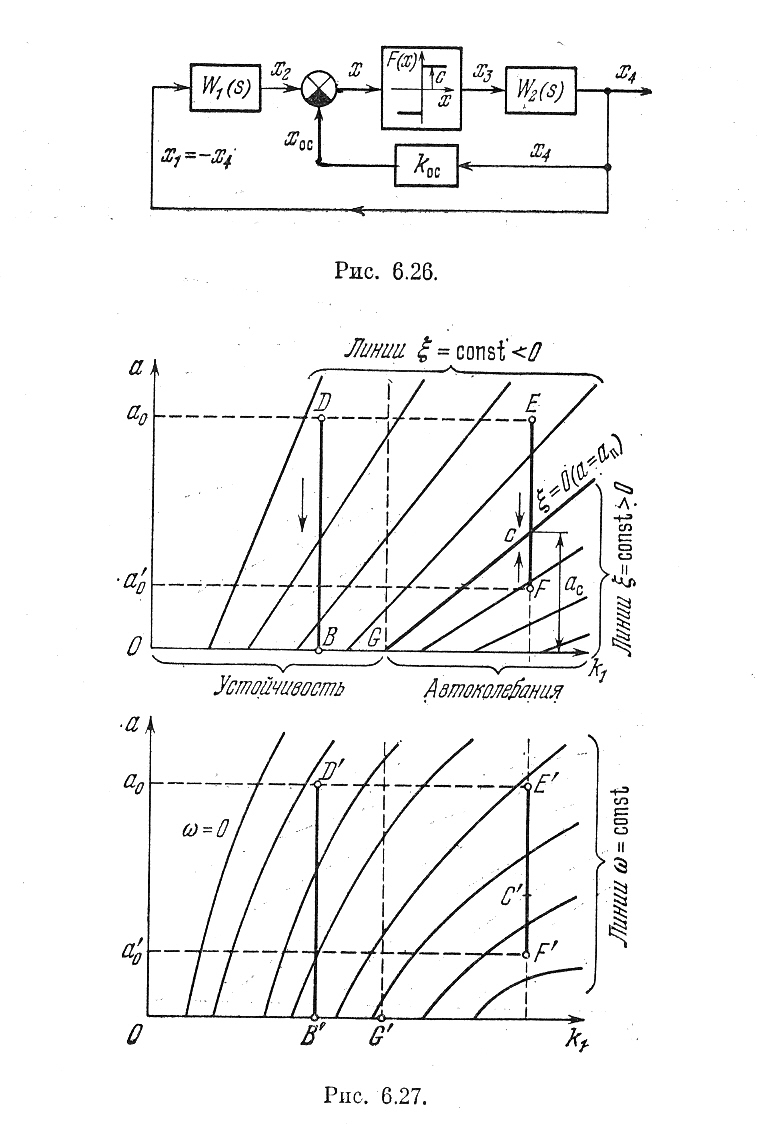
Рис. 6.26.

Рис. 6.27

Выделив вещественную и мнимую части, получим два уравнения (6.51) в виде

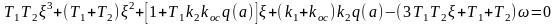
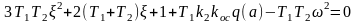
Из второго уравнения с учетом значения q(α) находим

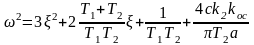(6.54)

а из первого

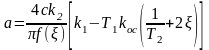(6.55)

где

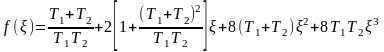
По формулам (6.54) и (6.55) построены диаграммы качества нелинейных колебательных переходных процес­сов в виде линий ξ = const и ω = const по параметру k₁ на рис. 6.27 и по параметру k_oc — на рис. 6.28

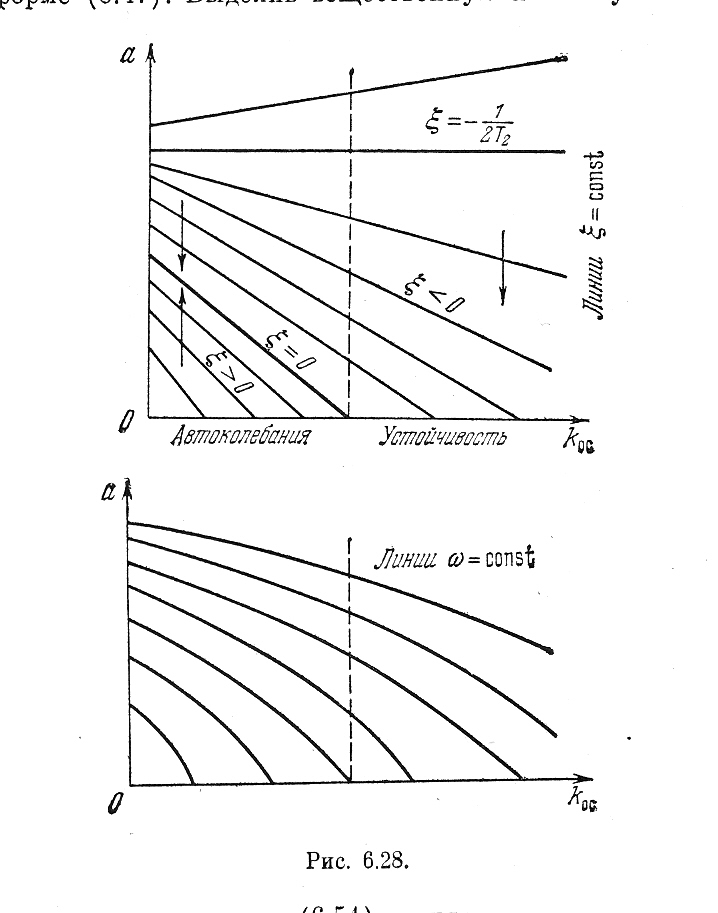
Рис. 6.28

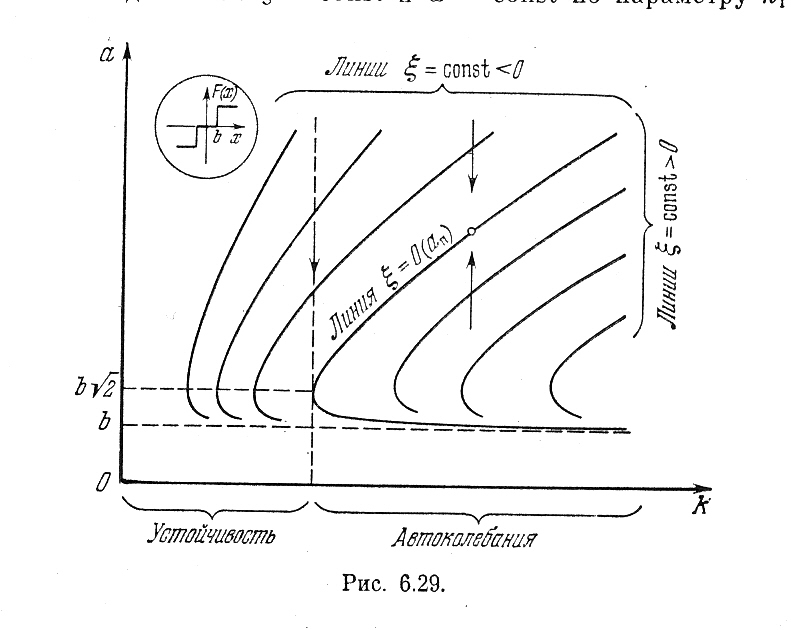
Рис. 6.29

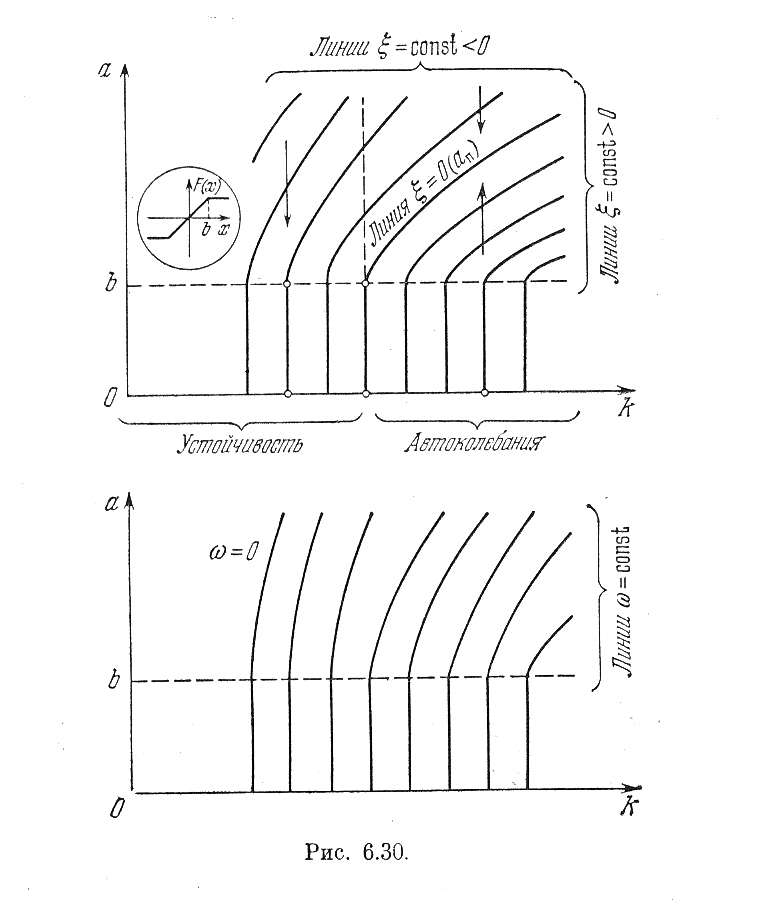
Рис.6.30

Нелинейная характеристика F(x) расположена в секто­ре [0, k_m] (рис. 6.31, б) и может иметь произвольное очертание. Данный способ оценки быстроты затухания

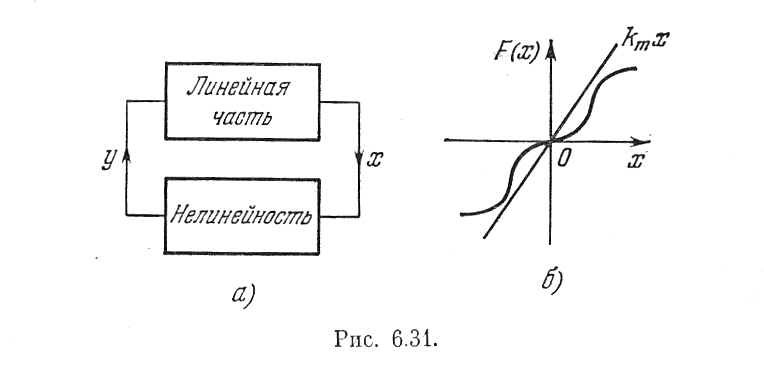
Рис 6.31

На комп­лексной плоскости вместо модифицированной (5.48) стро­ится смещенная частотная характеристика, определяе­мая следующим образом:

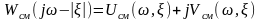(6.56)

где

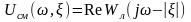
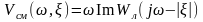
Можно определить предельное значение k_m, при ко­тором в системе имеет место показатель затухания, не меньше ‌‌, как показано на рис. 6.33.

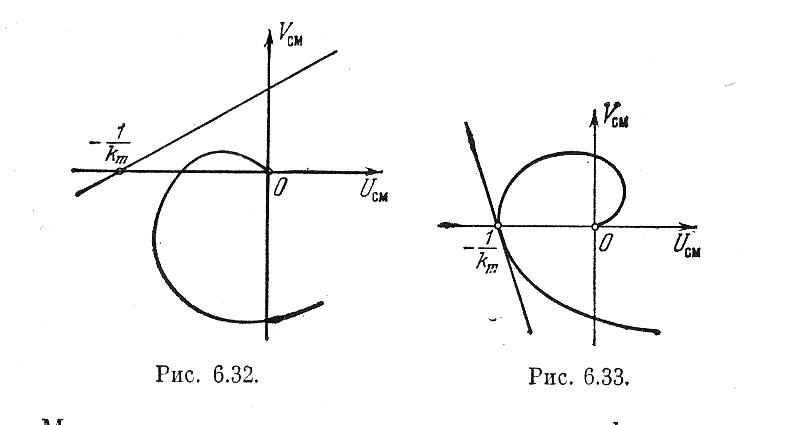
Рис.6.32 Рис.6.33

Если построить серию смещенных частотных харак­теристик для разных значений ξ, то получим зависи­мость ξ (k_m), т. е. зависимость показателя затухания от размера сектора, в котором лежит нелинейная характе­ристика.