
- •Глава 3. Методы припасовывания и точечного преобразования Метод припасовывания
- •Метод точечного преобразования
- •Примеры точечного преобразования
- •Глава 6. Процессы управления и вынужденные колебания в нелинейных системах Одночастотные вынужденные колебания. Частотные характеристики
- •Процессы управления, сопровождающиеся вынужденными вибрациями
- •Процессы управления в автоколебательных системах
- •Колебательные переходные процессы
Глава 6. Процессы управления и вынужденные колебания в нелинейных системах Одночастотные вынужденные колебания. Частотные характеристики
f(t)=Bsinωt (6.1)
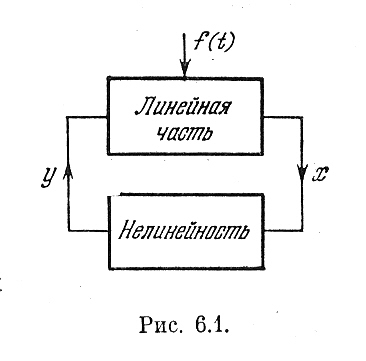
Рис.6.1
Уравнение динамики системы имеет вид
Q(p)x + R(p)F(x) = S(p)f(t) (6.2)
Решение для вынужденных колебаний будем искать приближенно в форме
x = αsin(ωt + φ) (6.3)
где ω задано, а неизвестными являются амплитуда α и фаза φ.
Произведем гармоническую линеаризацию нелинейности:
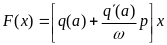 (6.4)
(6.4)
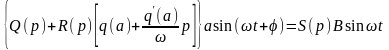 (6.5)
(6.5)
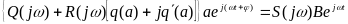
или
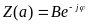 (6.6)
(6.6)
где
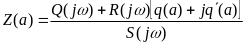 (6.7)
(6.7)
Уравнение (6.6) с двумя неизвестными α и φ можно решить графически
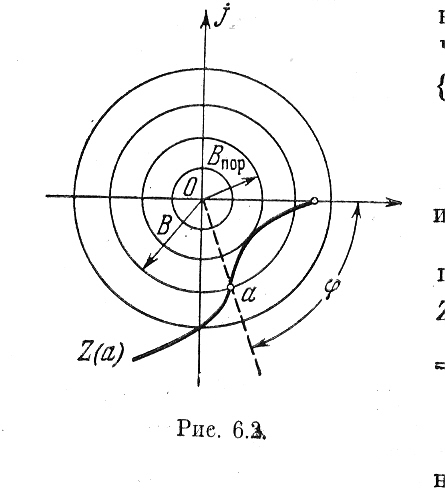 Рис.6.2
Рис.6.2
Рис. 6.3. Рис. 6.4.
На основании рис. 6.3 можно построить зависимости α(ω) и φ(ω), т. е. частотные характеристики замкнутой нелинейной системы по первой гармонике (6.3).
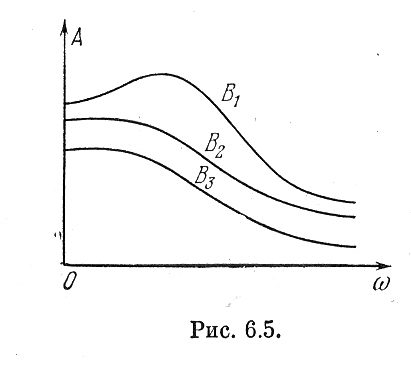
Рис.6.5
Пример. Пусть уравнение системы имеет вид
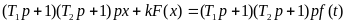
при гистерезисной нелинейности (рис. 6.6) и f(t)= Bsinωt. Тогда в уравнении (6.6), согласно (6.7), будем иметь
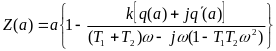
Для
заданной частоты
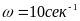 и заданных параметров системы k
= 10, с = 10, b
= 4, T1=
0,01, Т2
= 0,02, кривая Z(α) изображена на рис. 6.6,
где отмечены значения α .
и заданных параметров системы k
= 10, с = 10, b
= 4, T1=
0,01, Т2
= 0,02, кривая Z(α) изображена на рис. 6.6,
где отмечены значения α .
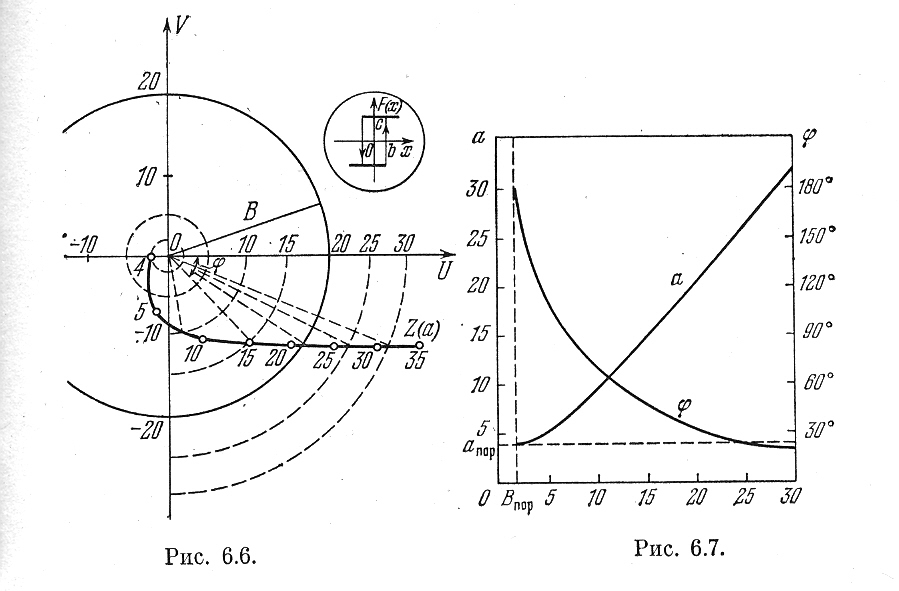
Рис. 6.6. Рис. 6.7.
Проведя окружности разных радиусов В, по точкам пересечения определим зависимости α(В) и φ(B) (рис. 6.7) для вынужденных колебаний при данной частоте.
Процессы управления, сопровождающиеся вынужденными вибрациями
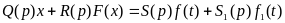 (6.8)
(6.8)
где
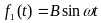 ,
a f(t)
— медленное по сравнению с
,
a f(t)
— медленное по сравнению с воздействие,
т. е. спектр возможных частот изменения
f(t) много меньше ω. Решение будем искать
в виде
воздействие,
т. е. спектр возможных частот изменения
f(t) много меньше ω. Решение будем искать
в виде
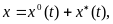
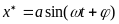 (6.9)
(6.9)
где
 —тоже
медленная по сравнению с x*(t) функция
времени, определяющая процесс управления
при наложенных на него вынужденных
вибрациях х*.
—тоже
медленная по сравнению с x*(t) функция
времени, определяющая процесс управления
при наложенных на него вынужденных
вибрациях х*.
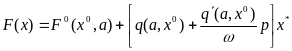 (6.10)
(6.10)
Для медленных составляющих (процесс управления) имеем
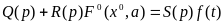 (6.11)
(6.11)
а для вибрационных составляющих
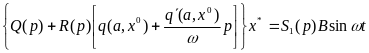 (6.12)
(6.12)
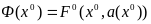 (6.13)
(6.13)
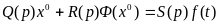 (6.14)
(6.14)
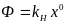
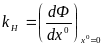 (6.15)
(6.15)
Но согласно (6.13) имеем
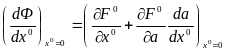 (6.16)
(6.16)
а согласно (4.16)
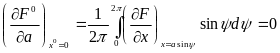 (6.17)
(6.17)
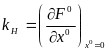
 Рис.
6.8.
Рис.
6.8.
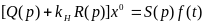
где
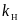 — коэффициент усиления нелинейности
в процессе управления, определяемый по
формуле (6.18). Например, для идеальной
релейной характеристики (см. раздел
4.2)
— коэффициент усиления нелинейности
в процессе управления, определяемый по
формуле (6.18). Например, для идеальной
релейной характеристики (см. раздел
4.2)
получим
F(x)
= csignx
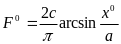
Получим
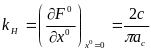
где
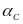 —
амплитуда симметричных вынужденных
колебаний в данной системе, найденных
согласно раздела 6.1.
—
амплитуда симметричных вынужденных
колебаний в данной системе, найденных
согласно раздела 6.1.
Для релейных характеристик с зоной нечувствительности и с петлей, дифференцируя (4.31), находим
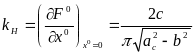

Рис.6.9. Рис.6.10.
На рис. 6.9 представлена зависимость коэффициента от амплитуды симметричных вынужденных колебаний.
Аналогично для релейной характеристики общего вида (рис. 6.10) получаем
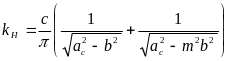
Для кусочно-линейной характеристики с зоной нечувствительности (рис. 6.11) имеем
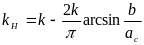
а для характеристики с насыщением (рис. 6.12)
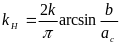 (ac
≥ b)
(ac
≥ b)
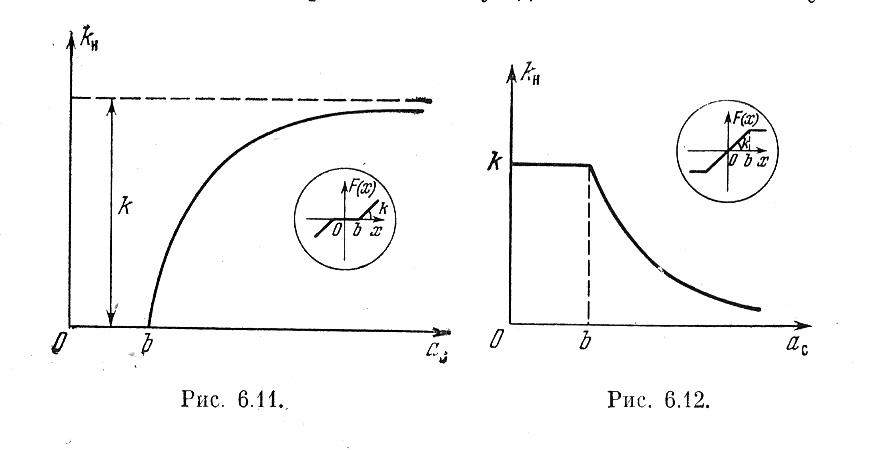
Рис.6.11. Рис.6.12.
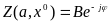
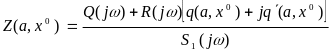
Задача 1.
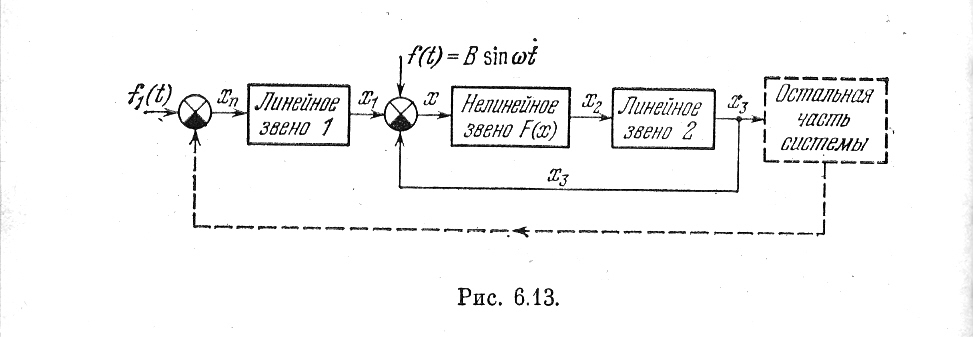
Рис. 6.13
Сигнал на входе нелинейности имеет вид
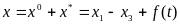
Причем
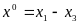
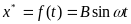
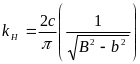 B
> b
B
> b
или же ликвидировать зону нечувствительности (рис. 6.11), получив
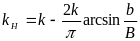 B
> b
B
> b
Задача 2.
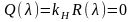
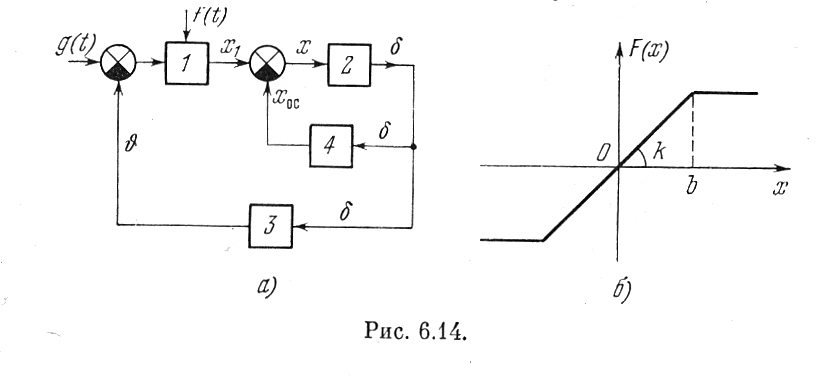
Рис. 6.14
Уравнение углового движения самолета по тангажу
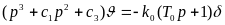
где
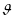 — отклонение самолета по тангажу, δ
— отклонение руля.
— отклонение самолета по тангажу, δ
— отклонение руля.
Уравнение измерителей
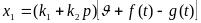
где f(t) = Вsinωt — вибрационная помеха
амплитуду симметричных вынужденных колебаний на входе нелинейности х можно вычислить по формуле
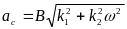
и для данной нелинейности (рис. 6.14,6), согласно (6.24), получаем
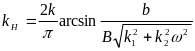 (6.28)
(6.28)
Уравнение привода руля для процесса управления вместо (6.27) примет вид
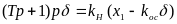
Характеристическое уравнение всей системы для процесса управления будет иметь пятую степень:
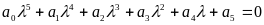
Предпоследний определитель Гурвица

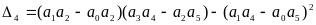
при некоторых числовых значениях параметров системы принимает вид
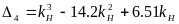
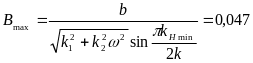
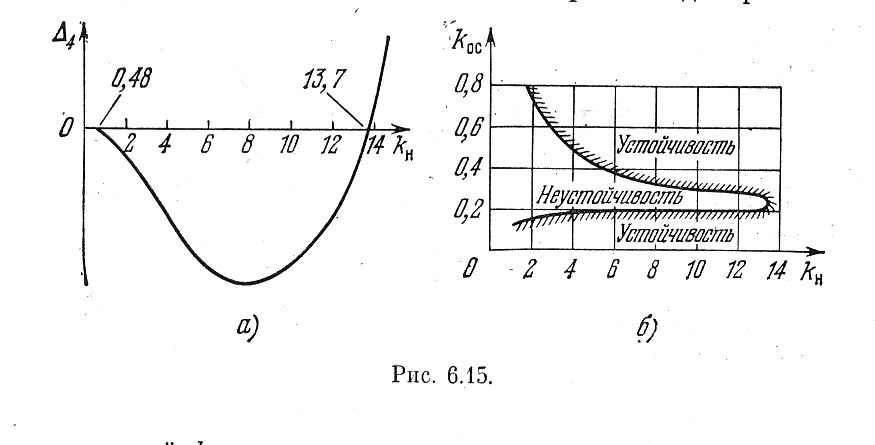
Рис.6.15.
