Глава 3. Методы припасовывания и точечного преобразования Метод припасовывания

Дана система, схема которой изображе­на на рис. 3.1,а, нелинейная характеристика F(x) регу­лятора представлена на рис. 3.1, б. Уравнение объекта:

уравнение регулятора:

Общее уравнение замкнутой системы имеет вид

(3.1)

Определение переходного процесса. Представим себе примерно возможный качественный вид процесса (рис. 3.2). Он разбивается на участки АВ, BD и т. д.,

Рис.3.1

внутри которых в соответствии с нелинейной характеристикой функция F(x) принимает постоянные значения +с или —с. Изобразим отдельно

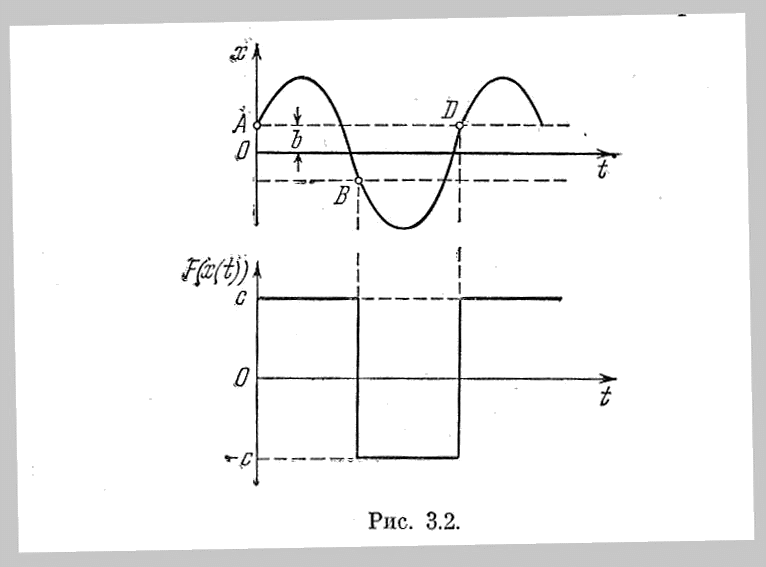
Рис.3.2

участки АВ и BD (рис. 3.3), отсчитывая время t на каждом из них от нуля.

На участке АВ, согласно (3.1), уравнение системы

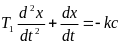
имеет первый интеграл в виде

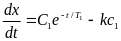(3.2)

а второй —

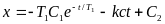(3.3)

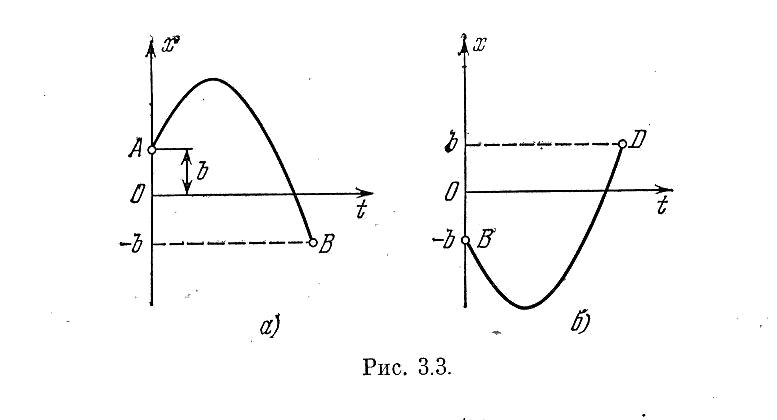
Рис.3.3

Определение периодического решения (автоколеба­ний).

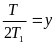
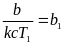
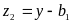
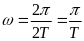
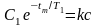
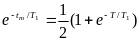
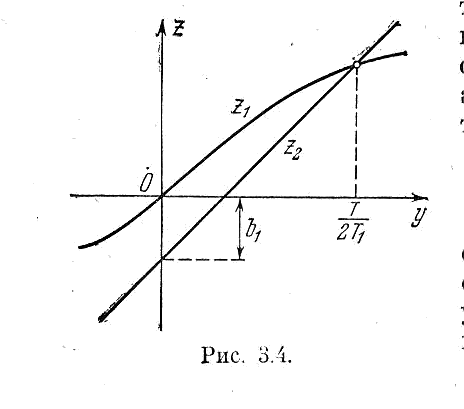
Рис.3.4

Далее по формуле (3.3) определим амплитуду автоко­лебаний:

где С₁ известно из (3.9). В результате формула

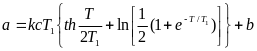
позволяет вычислить и амплитуду автоколебаний.

Метод точечного преобразования

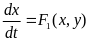
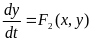(3.12)

Зависимость 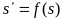(3.13) ,

соответствующая ходу фазовой траектории в силу реше­ния уравнений (3.12), называется функцией последова­ния. Функция последования определяет закон точечного преобразования для данной нелинейной системы.

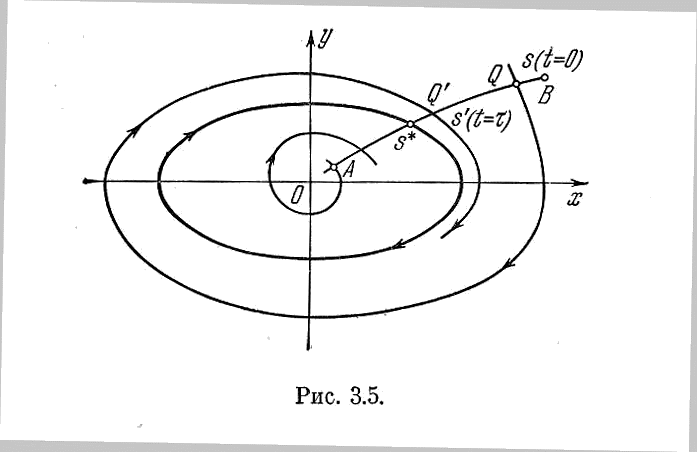
Рис.3.5.

Определение последующих точек по заданным исход­ным на отрезке АВ и называется точечным преобразова­нием отрезка АВ самого в себя. Ввиду непрерывности расположения фазовых траекторий исходные и последую­щие точки заполняют весь отрезок. Однако каждая точка отрезка АВ не обязательно имеет последующую внутри этого отрезка. Фазовые траектории, пересекающие отре­зок, могут и не возвращаться к нему.

Возможен такой случай, что последующая точка Q' совпадает с исходной Q, т. е.

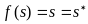(3.14)

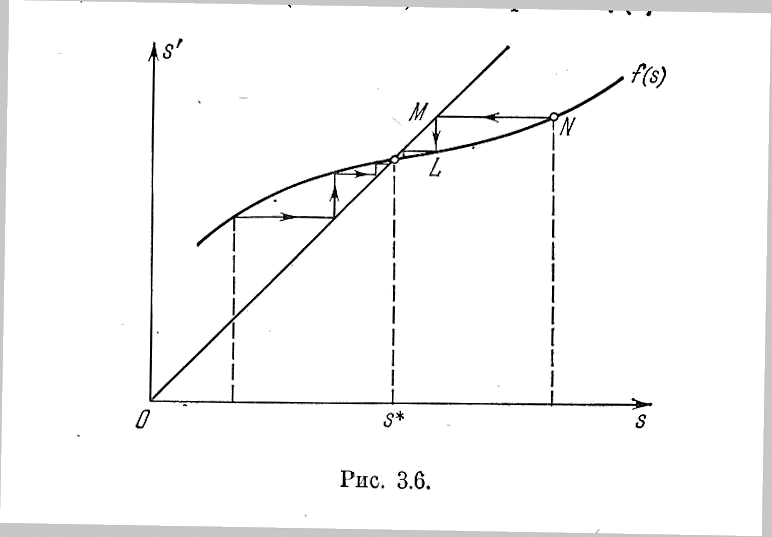
Рис.3.6

условие устойчивости предельного цикла имеет вид

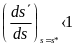(3.15)

На других гра­фиках рис. 3.7 показаны: б) случай двух предельных циклов, из которых один неустойчивый, а второй устой­чивый;

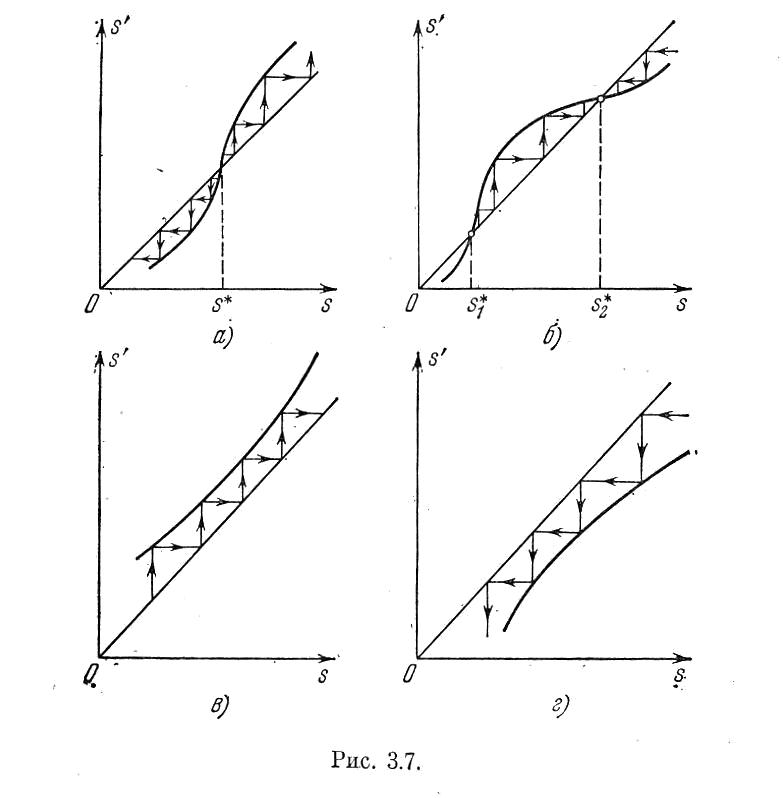
Рис.3.7

в) случай расходящихся колебаний; г) случай затухающих колебаний.

Такого типа графики (рис. 3.6, 3.7) называются ди­аграммами точечного преобразования.

В большинстве случаев бывает легче представить функцию последования в параметрической форме.

Рис. 3.8

Параметрическая фор­ма точечного преобра­зования в качестве параметра содержит вре­мя 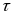прохождения изо­бражающей точки по фазовой траектории от исходной точки Q (рис. 3.5) до ее после­дующей Q'. Через этот параметр на основа­нии решения урав­нений (3.12) выражаются координаты точек Q и Q', а именно

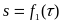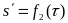, (3.16)

Весь ход точечного преобразования показан на рис. 3.8 стрелками.

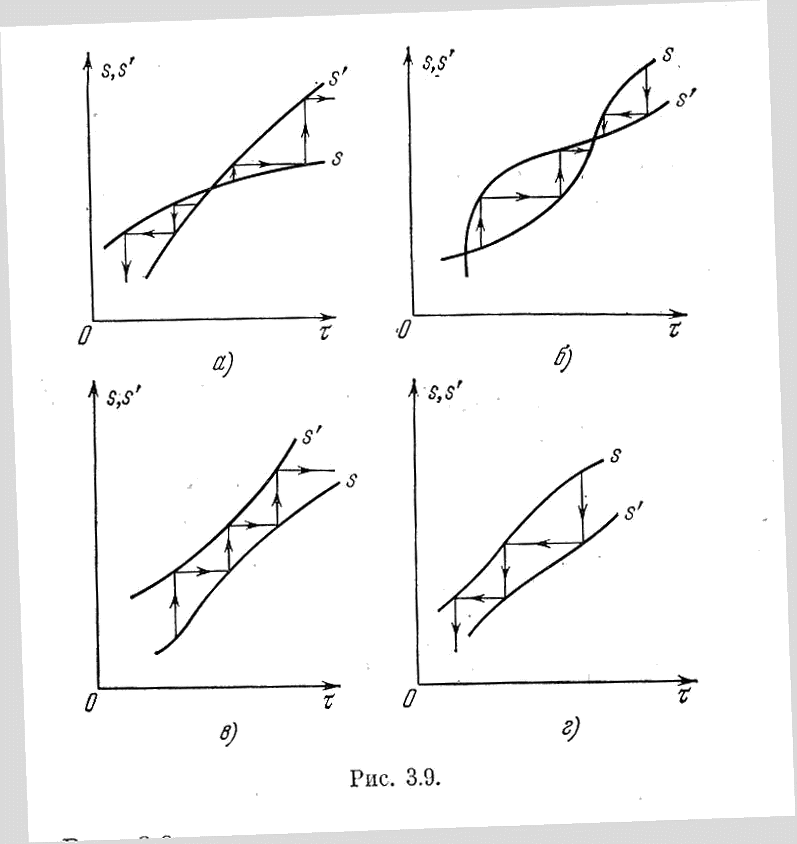
Рис. 3.9.

Рис. 3.9 иллюстрирует параметрические диаграммы точечного преобразования для тех же четырех случаев, что и на рис. 3.7.