§1.21. Дифференцирующее звено.

Дифференцирующем называют звено, у которого в установившемся режиме выходная величина пропорциональна дифференциалу входной величены.

1.62

Или в операторной форме:

1.63

В реальных условиях не существует такого реального элемента, который бы на выходе точно воспроизводил бы производную от входного сигнала. Идеализированными примерами такого звена могут быть:

а) Тахогенератор.

б) Ток через электроконденсатор.

Передаточная функция этого звена:

1.64

Переходная функция:

1.65

Весовая функция:

1.66

Частотные характеристики:

1.67

1.68

Вид частотных характеристик:

АФХ АЧХ ФЧХ

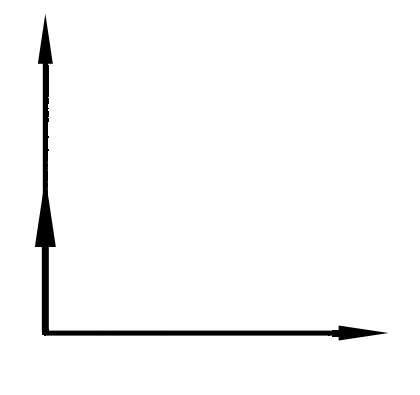
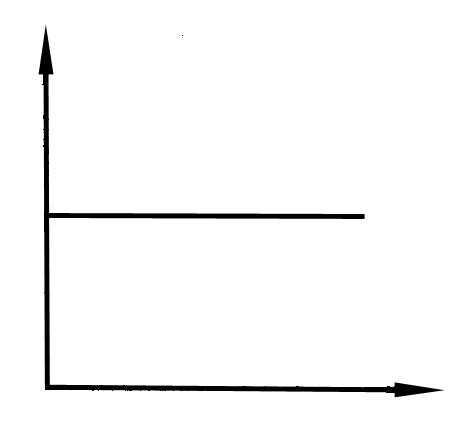
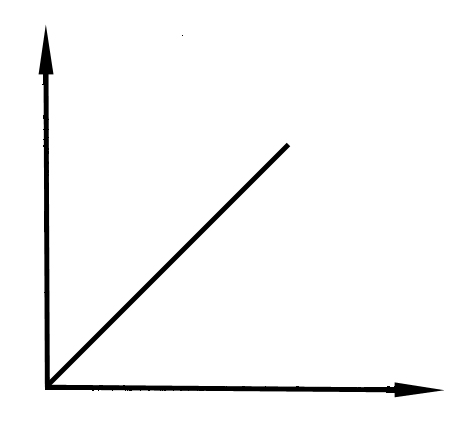
Логарифмические частотные характеристики:

1.69

Вид логарифмических характеристик:

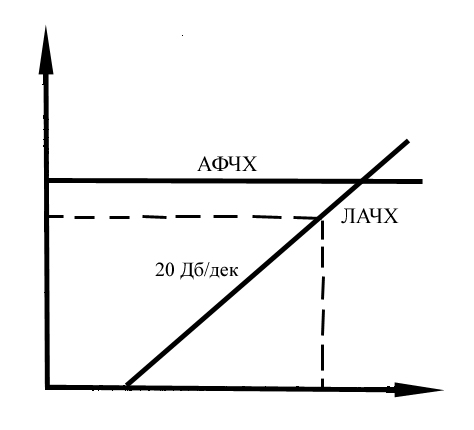
§1.22 Апериодическое (инерционное) звено первого порядка.

Апериодическим называется такое звено, у которого выходная величина после подачи на вход ступенчатого воздействия изменяется монотонно, достигая некоторого установившегося значения.

1.70

Дифференциальное уравнение в операторной форме

1.71

Апериодические звенья первого порядка наиболее часто применяются в практике автоматического регулирования.

Примеры звеньев:

1)нагрев тела

2)RC-цепь

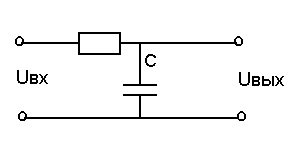
Передаточная функция

1.72

Переходная функция

1.73

Функция веса

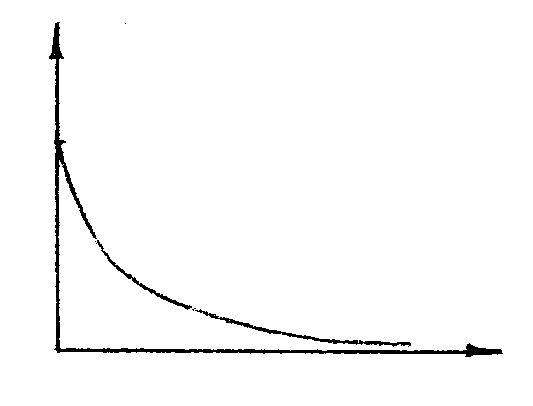
1.74

Для рассматриваемого звена временной характеристикой может служить решение дифференциального уравнения (1.70).

1.75

Из выражения (1.75) можно перейти к выражению (1.73), если на вход подать ступенчатое воздействие, а начальные координаты принять равные нулю.

Теоретически, переходный процесс у звеньев рассматриваемого типа, длится бесконечно долго. Практически же, для апериодического звена, переходный процесс может быть завершенным, если выходная величина достигает значения 0,95-0,99 от установившегося. Такой промежуток времени определяется значениями (3Т...5Т).

Частотные характеристики

1.76

1.77

Вид частотных характеристик

АФХ АЧХ ФЧХ

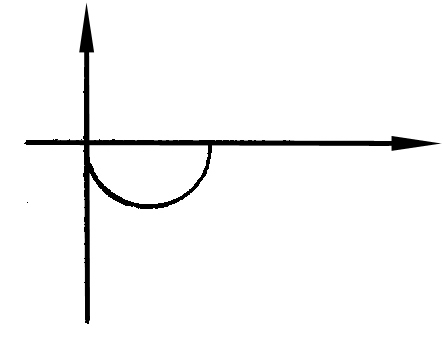
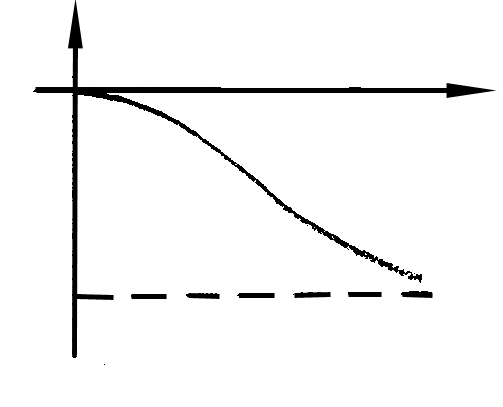
Выражение для ЛАЧХ

1.78

Выражение для аналитической ЛАЧХ

1.79

Вид логарифмических характеристик

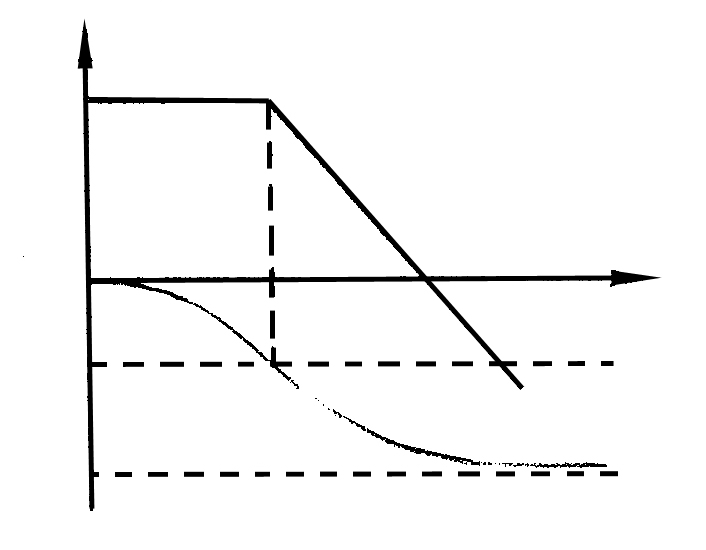
§1.23 Колебательное звено.

Колебательное звено в динамическом режиме описывается операторным уравнением

где Т₁ и Т₂ – постоянные времени, характеризующие период и время затухания собственных колебаний звена (при Т₁ <2Т₂);

к – коэффициент усиления звена.

Колебательное звено отличается тем, что при изменении входной величины x возникает колебательный процесс изменения выходной величины y. Уравнение передаточной функции и АФЧХ колебательного звена выражается аналогично как и для апериодического звена второго порядка.

Временная характеристика

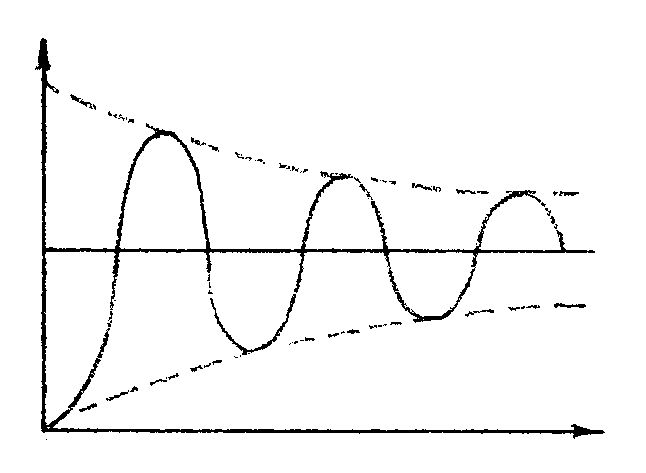
АФЧХ при входном воздействии типа единичного скачка

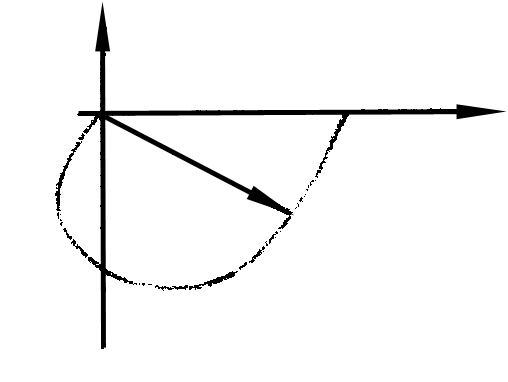
Колебательное звено можно рассматривать как соединение двух емкостей, способных записать энергию или вещество и взаимно обмениваться этими запасами при возмущениях, нарушающих равновесие звена возникшего колебания. Если в результате колебания происходит потеря энергии в звене, то колебания затухают, а само звено называется устойчивым.

Выше речь шла об устойчивом колебательном звене. Если же при колебаниях запас энергии в звене увеличивается, то амплитуда колебания возрастает, а само звено называется неустойчивым. Уравнение динамики неустойчивого колебательного звена в операторной форме