6.5 Выражения для функции нормального распределения и плотности нормального распределения
В общем виде выражения для функции нормального распределения и плотности нормального распределения выглядят следующим образом:
,
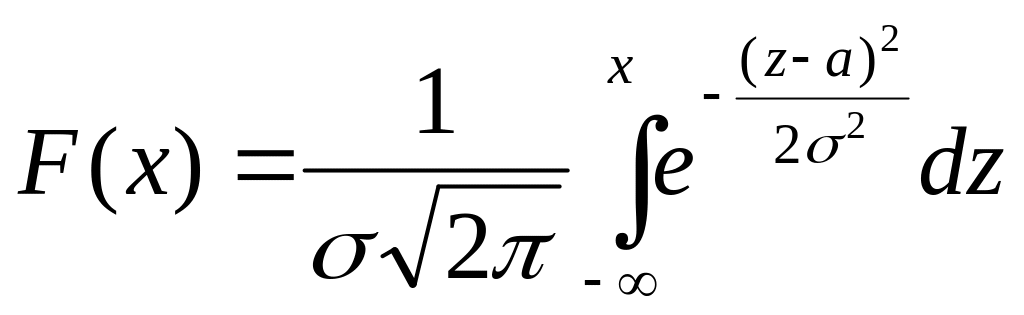
где
- математическое ожидание,
- среднее квадратичное отклонение
нормального распределения.
Запишем данные выражения для нашей
выборки при
,
:
Построим график функции нормального распределения на ЭФР (рис. 4.) и график функции плотности нормального распределения на гистограмме (рис. 5.).
VII. Доверительные интервалы
7.1 Доверительные интервалы для математического ожидания и дисперсии
7.1.1 По исходным данным
Исходными данными будем считать выборку после удаления резко выделяющихся значений, объем которой (см. таблицу 3)
При построении доверительных интервалов по исходным данным объем выборки достаточно большой, поэтому доверительные интервалы для математического ожидания и дисперсии запишутся в следующем виде:
,
где
- квантиль нормального распределения,
=0,9;
0,95; 0,99 – доверительная вероятность,
- уровень значимости.
Для исходной выборки:
Квантили нормального распределения [3] для доверительной вероятности =0,9; 0,95; 0,99 приведены в таблице 9.
Таблица 9
Квантили нормального распределения
-
0,9
0,1
0,05
1,645
0,95
0,05
0,025
1,96
0,99
0,01
0,005
2,576
Запишем доверительные интервалы для математического ожидания для доверительных вероятностей =0,9; 0,95; 0,99:
,
,
,
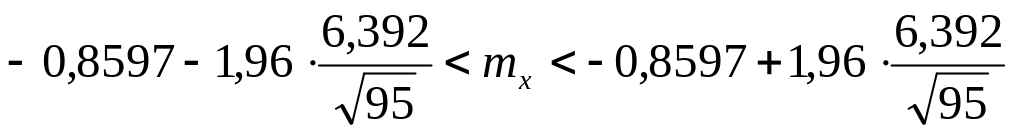Запишем доверительные интервалы для дисперсии для доверительных вероятностей =0,9; 0,95; 0,99:
,
,
,
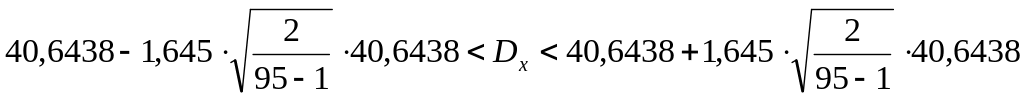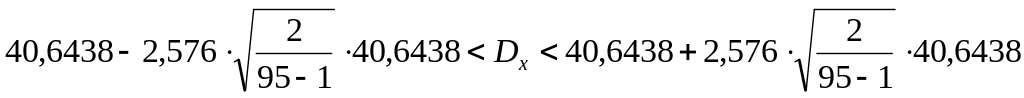7.1.2 По второй строке исходных данных
Второй строкой исходных данных будем считать вторую строку заданной выборки не отсортированной по возрастанию (см. задание на курсовую работу) без резко выделяющихся значений (таблица 10):
Таблица 10
Вторая строка исходных данных без РВЗ
6,6 |
0,14 |
-2,35 |
-0,85 |
-9,21 |
-13,91 |
10,28 |
-9,29 |
13,29 |
Такая выборка является выборкой малого объема, поэтому доверительные интервалы для математического ожидания и дисперсии будем вычислять по формулам:
,
где
- квантиль распределения Стьюдента [1]
с
степенями свободы,
и
- квантили распределения Пирсона [1] с
степенями свободы,
=0,9;
0,95; 0,99 – доверительная вероятность,
- уровень значимости.
Для данной выборки:
Результаты расчетов приведены в приложении 4.
Квантили распределения Стьюдента и Пирсона для доверительной вероятности =0,9; 0,95; 0,99 приведены в таблице 11.
Таблица 11
Квантили распределения Стьюдента и Пирсона
|
|
|
|
|
|
|
0,9 |
0,1 |
0,05 |
0,95 |
1,8595 |
15,507 |
2,733 |
0,95 |
0,05 |
0,025 |
0,975 |
2,306 |
17,535 |
2,18 |
0,99 |
0,01 |
0,005 |
0,995 |
3,3554 |
21,955 |
1,344 |
Запишем доверительные интервалы для математического ожидания для доверительных вероятностей =0,9; 0,95; 0,99:
,
,
,
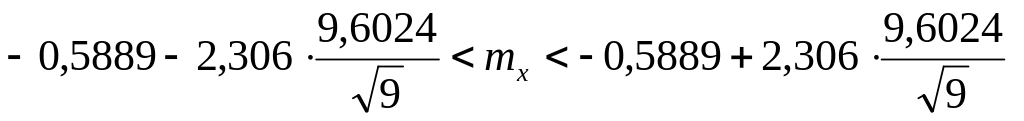Запишем доверительные интервалы для дисперсии для доверительных вероятностей =0,9; 0,95; 0,99:
,
,
,
