4.2 Предположение о виде закона распределения, о рвз

По виду эмпирической функции распределения (рис. 4.) и гистограмме частот (рис. 5.) можем предположить, что данная выборка подчиняется нормальному закону распределения. По виду гистограммы (см. рис. 5.) видно, что в выборке отсутствуют грубые ошибки эксперимента, т.е. нет резко выделяющихся значений, это свидетельствует и о том, что проверка на РВЗ произведена правильно.

V. Оценки числовых характеристик случайной величины для выборки без рвз

5.1 Смещенные и несмещенные оценки числовых характеристик

Несмещенной называют статистическую оценку , математическое ожидание которой равно оцениваемому параметру при любом объеме выборки, т.е. .

Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Объем выборки .

Рассчитаем оценки положения центра данных: оценку математического ожидания, оценку медианы (выборочную медиану) – по следующим формулам:

Сравнение среднего арифметического значения и выборочной медианы позволяет сделать следующий вывод: так как ( ), то это говорит о том, что закон распределения симметричный (это хорошо видно на гистограмме рис. 5.).

Рассчитаем оценки характеристик рассеивания:

3. оценки дисперсии:

- смещенная оценка

- несмещенная оценка

4. оценки среднего квадратичного отклонения:

- смещенная оценка

- несмещенная оценка

- поправочный коэффициент, тогда

- робастная оценка

- медиана абсолютных отклонений (МАО)

Сравнение робастной оценки среднего квадратичного отклонения и несмещенной оценки позволяет сделать следующий вывод: так как робастная и несмещенная оценки практически не отличаются друг от друга ( ), то можно сказать, что закон распределения очень близок к нормальному, нет резко выделяющиеся значения (что и видно по рис. 5.).

Рассчитаем оценки распределения характеристики формы кривой распределения:

5. оценка начальных моментов:

Рассчитаем оценки для .

6. оценки центральных моментов:

- смещенная оценка

Несмещенная оценка:

7. оценки коэффициента асимметрии:

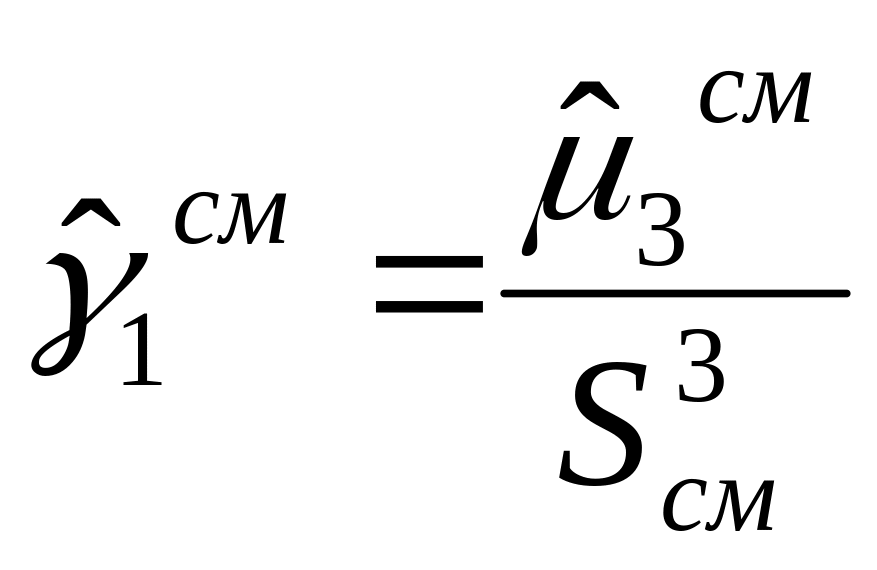- смещенная оценка

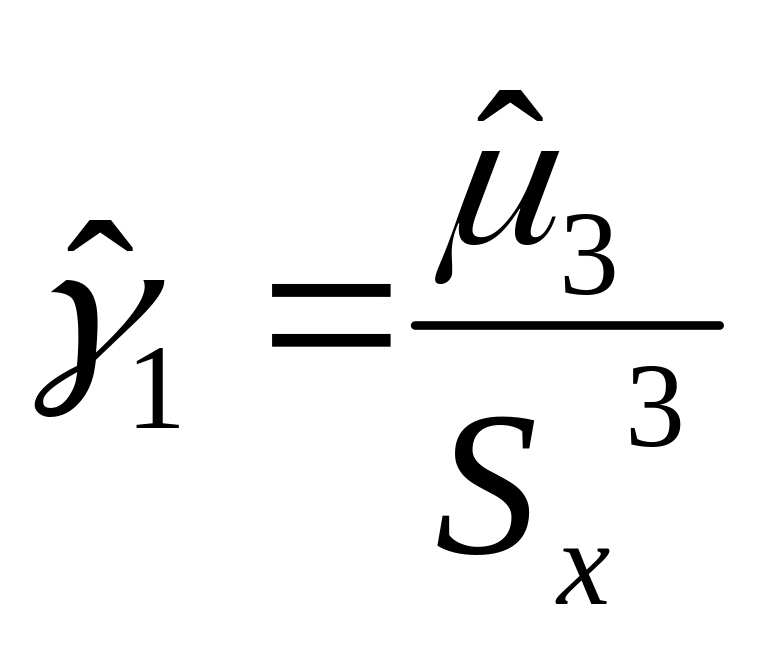- несмещенная оценка

8. оценки коэффициента эксцесса:

- смещенная оценка

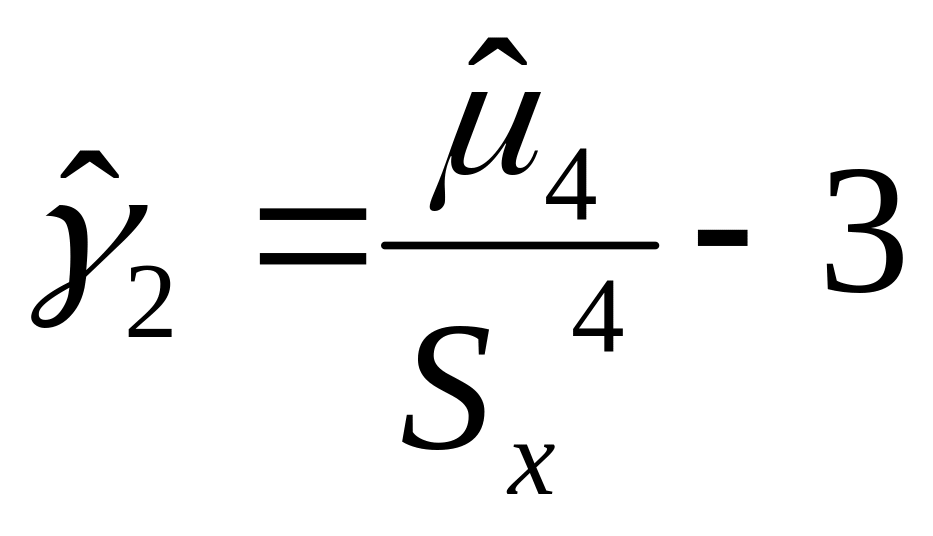- несмещенная оценка

Результаты расчетов, выполненных с помощью Microsoft Excel, приведены в приложении 2.

5.2 Относительные ошибки между смещенными и несмещенными оценками

Относительные ошибки, между смещенными и несмещенными оценками можно вычислить по следующей формуле:

Расчеты представим в виде таблицы (таблица 5):

Таблица 5

Относительные ошибки между смещенными и несмещенными оценками

Несмещенные оценки	40,6438	6,392		40,6437	45,1194	5342,4347	0,1728	0,2003
Смещенные оценки	40,2159	6,3752		40,2159	43,7046	5220,189	0,1687	0,1602
Относительная ошибка	1,064%	0,264%	0%	1,0638%	3,2372%	2,3418%	2,4303%	25,0312%

Относительные ошибки между смещенными и несмещенными оценками числовых характеристик получились сравнительно небольшими, они в основном обусловлены большим объемом выборки. Относительная ошибка для коэффициента эксцесса довольно большая (25,0312%). Причиной этому может быть увеличение ошибки между смещенной и несмещенной оценками среднего квадратичного отклонения в формулах оценок коэффициента эксцесса ( , ) .