3.2 Проверка выборки на рвз по робастному правилу

Когда закон распределения заметно отличается от нормального, применяются робастные правила удаления резко выделяющихся значений. Робастные правила основаны на робастных оценках центра данных.

Алгоритм удаления РВЗ по робастному правилу:

1. Находим выборочную медиану , которая делит вариационный ряд на две равные части по количеству элементов, по формуле:

2. Находим медиану абсолютных отклонений (МАО) - , где

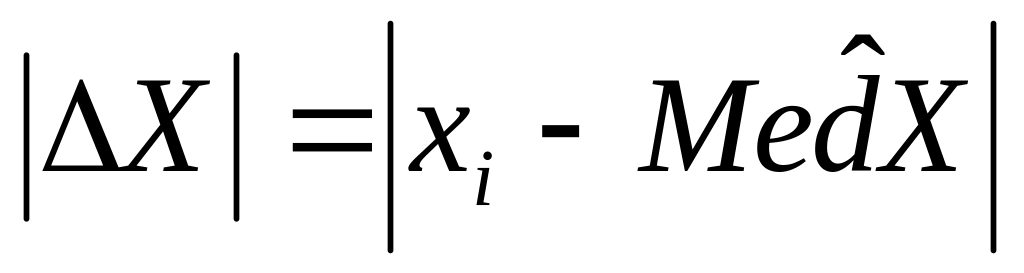
3. Рассчитываем интервал, за пределом которого данные будут считаться резко выделяющимися значениями:

Данный алгоритм нужно повторять до тех пор, пока все элементы выборки не войдут в интервал.

Проверим заданную выборку на РВЗ по данному правилу.

1. Находим выборочную медиану , которая делит вариационный ряд на две равные части по количеству элементов:

- - четное

2. Находим медиану абсолютных отклонений - :

   1. 

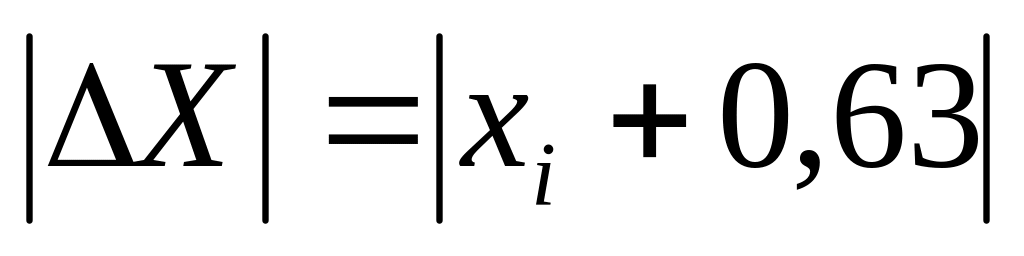
   2. Сортируем полученную выборку по возрастанию

   3. 

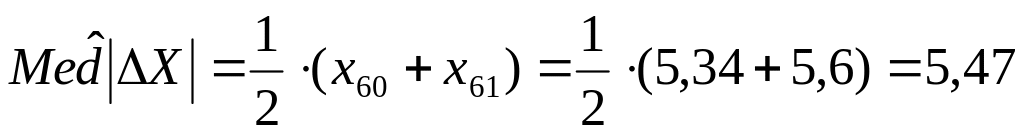
      3. Рассчитываем интервал:

В данный интервал не вошли 13 элементов выборки, т.е. можно считать эти элементы резко выделяющимися значениями. Новый объем выборки составляет .

Данный алгоритм пришлось повторить 7 раз, прежде чем все элементы выборки вошли в рассчитанный интервал. Объем выборки без РВЗ составил :

1. - - нечетное

2. 

3. 

- все 95 элементов вошли в данный интервал.

Следовательно, по робастному правилу получили, что объем выборки без РВЗ составляет .

3.3 Выводы по проверке выборки на резко выделяющиеся значения

Сравним результаты, полученные при использовании классического правила для проверки выборки на РВЗ и робастного правила.

Проверка выборки на резко выделяющиеся значения по классическому правилу показала, что в исходной выборке есть РВЗ, выборка без РВЗ составила . Проверка по робастному правилу также показала, что в исходной выборке есть РВЗ, но выборка без РВЗ составила . В итоге получили два различных объема выборки без резко выделяющихся значений.

Так как по классическому правилу мы не достигли такого значения , при котором бы выполнялось условие , а лишь можем предположить, что при значение - не РВЗ, то можем сделать вывод, что классическое правило дало только приблизительные результаты. Робастное правило, как упоминалось выше, применяется когда закон распределения заметно отличается от нормального, что можно без труда заметить на рисунке, где изображена гистограмма частот исходной выборки (см. рис. 2.). Также важно отметить, что робастное правило дало более точный результат по объему выборки.

Исходя из этих размышлений, я предпочла использовать далее объем выборки, полученный из проверки на РВЗ по робастному правилу, т.е. .

Так как в исходной выборке после проверок были обнаружены резко выделяющиеся значения, необходимо вновь уже для выборки без РВЗ ( ) построить эмпирическую функцию распределения, гистограмму, полигон частот, найти оценки числовых характеристик случайной величины.

IV. Эмпирические распределения случайной величины для выборки без рвз

4.1 Построение эмпирической функции распределения, гистограммы и полигона частот

Для построения эмпирической функции распределения случайной величины, гистограммы и полигона частот для заданной выборки объемом выполним следующие расчеты:

1. Отсортированная выборка без РВЗ представлена в таблице 3.

Таблица 3

Выборка без РВЗ, отсортированная по возрастанию

-16,22	-14,69	-13,91	-11,87	-11,01	-10,98	-10,56	-10,22	-9,65	-9,29
-9,21	-8,89	-8	-7,38	-7,37	-7,37	-6,34	-6,28	-6,23	-5,97
-5,95	-5,09	-4,65	-4,56	-4,26	-4,13	-4,07	-3,95	-3,73	-3,42
-3,28	-3,1	-2,91	-2,68	-2,35	-1,81	-1,77	-1,6	-1,6	-1,45
-1,44	-1,42	-1,09	-1,07	-0,86	-0,85	-0,85	-0,81	-0,73	-0,68
-0,58	-0,42	-0,34	-0,25	-0,04	0	0,08	0,11	0,14	0,17
0,28	0,95	0,97	1,03	1,16	1,21	1,5	1,51	1,52	1,65
1,68	1,86	2,69	3,16	3,4	3,63	4,08	4,16	4,67	5,13
5,14	5,71	5,82	6,47	6,6	7,11	7,15	9,75	10,09	10,28
11,65	12,48	12,72	13,29	16,56

2. Разобьем весь диапазон наблюдаемых значений на интервалы. Рассчитаем количество интервалов по следующей формуле:

Так как , то

3. Определим размах выборки . Для данной выборки (см. таблицу 3) , , тогда:

4. Находим ширину интервалов (шаг) по формуле:

Так как , , то

5. Границы интервалов найдем по формулам:

6. Находим количество точек, попавших в i-ый интервал - частоты .

7. Находим середину i-ого интервала .

8. Для каждого интервала находим накопленные частоты:

9. Определим относительную частоту i-ого интервала по формуле:

10. Для каждого интервала находим относительные накопленные частоты по следующей формуле:

11. Для i-ого интервала находим оценку плотности вероятности:

Результаты расчетов приведены в таблице 4.

Таблица 4

Результаты расчетов для построения ЭФР, гистограммы и полигона частот

№
1	[-16,22; -11,5371)	4	-13,87855	4	0,0421	0,0421
2	[-11,5371; -6,8542)	12	-9,19565	16	0,1263	0,1684
3	[-6,8542; -2,1713)	19	-4,51275	35	0,2	0,3684
4	[-2,1713; 2,5116)	37	0,17015	72	0,3895	0,7579
5	[2,5116; 7,1945)	15	4,85305	87	0,1579	0,9158
6	[7,1945; 11,8774)	4	9,53595	91	0,0421	0,9579
7	[11,8774; 16,5603]	4	14,21885	95	0,0421	1

Графиком эмпирической функции распределения (ЭФР) случайной величины является ступенчатая функция. График полученной ЭФР показан на рис. 4.

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии . Гистограмма частот для данной выборки изображена на рис. 5.

Для построения полигона частот на оси абсцисс откладывают варианты , а на оси ординат – соответствующие им частоты . Точки соединяют отрезками прямых и получают полигон частот. Полигон частот заданной выборки показан на рис. 6.