Проверка гипотезы
Выдвинем нулевую гипотезу и конкурирующую ей:
Заданы две выборки:
Первая выборка :
16,56 |
13,29 |
-8 |
-6,28 |
-0,04 |
3,4 |
4,67 |
-4,56 |
1,65 |
6,47 |
-3,1 |
Вторая выборка :
-10,98 |
0,11 |
-1,77 |
7,11 |
-11,87 |
-4,13 |
-7,38 |
-3,1 |
Найдем
средние арифметические
выборки, объем которой
и
выборки, объем которой
:
В качестве проверки нулевой гипотезы о равенстве математических ожиданий двух нормальных совокупностей с неизвестными, но одинаковыми дисперсиями (как показала проверка гипотезы об однородности дисперсий, сделанная в предыдущем пункте) необходимо вычислить наблюдаемое значение критерия:
,
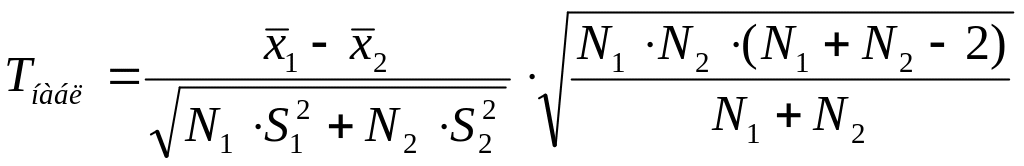при , , которые были вычислены ранее.
Так как конкурирующая гипотеза имеет
вид
,
поэтому критическая область -
правосторонняя, находим по таблице
критических точек распределения
Стьюдента [1] при уровне значимости
=
0,01; 0,05; 0,1 критическую точку
,
где
- число степеней свободы (см. таблицу
22).
Таблица 22
-
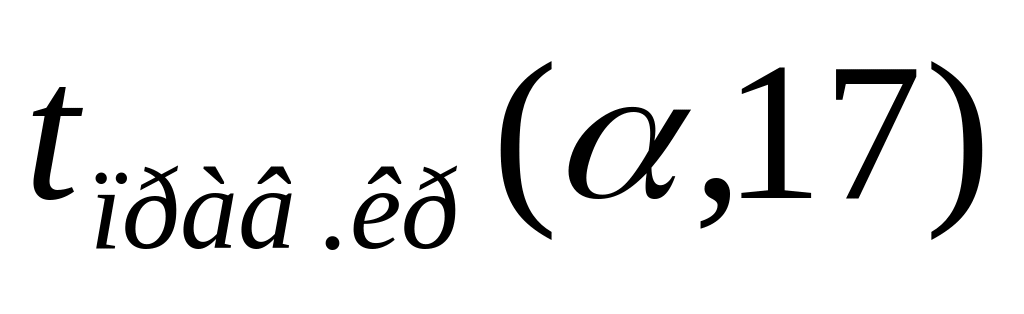
0,01
2,5669
0,05
1,7396
0,1
1,3334
Так как
,
то для уровней значимости
=
0,05; 0,1 нулевую гипотезу о равенстве
математический ожиданий отвергаем, а
для уровня значимости
=
0,01 эту гипотезу принимаем, так как в
этом случае
.
Список использованной литературы
Большев Л. Н., Смирнов Н. В. Таблицы математической статистики. – М.: Наука. Главная редакция физико-математической литературы, 1983. – 416 с.
Вентцель Е. С. Теория вероятностей: Учеб. для вузов. – 5-е изд. стер. – М.: Высш. шк., 1998. – 576 с.: ил.
Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов. Изд. 5-е, стер. – М.: Высш. шк., 2001. – 400 с.: ил.
Гмурман В. Е. Теория вероятностей и математическая статистика. Учеб. пособие для вузов. Изд. 7-е, стер. – М.: Высш. шк., 1999. – 479 с.: ил.