Содержание

I. Эмпирические распределения случайной величины 5

1.1 Построение эмпирической функции распределения, гистограммы и полигона частот 5

1.2 Предположение о виде закона распределения, о РВЗ 7

II. Оценки числовых Характеристик случайной величины 10

2.1 Смещенные и несмещенные оценки числовых характеристик 10

III. Проверка выборки на резко выделяющиеся значения 14

3.1 Проверка выборки на РВЗ по классическому правилу 14

3.2 Проверка выборки на РВЗ по робастному правилу 16

3.3 Выводы по проверке выборки на резко выделяющиеся значения 18

IV. Эмпирические распределения случайной величины для выборки без РВЗ 19

4.1 Построение эмпирической функции распределения, гистограммы и полигона частот 19

4.2 Предположение о виде закона распределения, о РВЗ 21

V. Оценки числовых характеристик случайной величины для выборки без РВЗ 24

5.1 Смещенные и несмещенные оценки числовых характеристик 24

5.2 Относительные ошибки между смещенными и несмещенными оценками 27

VI. Проверка гипотезы о законе распределения случайной величины 28

6.1 Подходящий закон распределения 28

6.2 Критерий Пирсона 29

6.3 Критерий Колмогорова 31

6.4 Критерий 33

6.5 Выражения для функции нормального распределения и плотности нормального распределения 34

VII. Доверительные интервалы 35

7.1 Доверительные интервалы для математического ожидания и дисперсии 35

7.1.1 По исходным данным 35

7.1.2 По второй строке исходных данных 36

7.2 Сравнение доверительных интервалов 39

7.3 Доверительные интервалы для функции распределения 39

VIII. Теоретические числовые характеристики распределения 41

8.1 Числовые характеристики случайной величины 41

8.2 Сравнение теоретических числовых характеристик с их оценками 42

IX. Однофакторный дисперсионный анализ 44

9.1 Проверка выхода на нормальный закон распределения 45

9.2 Средние и дисперсии по уровням 46

9.3 Проверка однородности дисперсий по партиям 47

9.4 Общая дисперсия, дисперсия фактора, дисперсия помехи 49

9.5 Проверка значимости входного фактора 51

X. Гипотезы о числовых характеристиках 52

Список использованной литературы 58

I. Эмпирические распределения случайной величины

0. 1.1 Построение эмпирической функции распределения, гистограммы и полигона частот

Эмпирической функцией распределения (функцией распределения выборки) называют функцию , определяющую для каждого значения относительную частоту события . По определению, , где - число вариант, меньших ; - объем выборки.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною , а высоты равны отношению .

Полигоном частот называют ломаную, отрезки которой соединяют точки .

Для построения эмпирической функции распределения случайной величины, гистограммы и полигона частот для заданной выборки объемом выполним следующие расчеты:

1. Отсортируем выборку по возрастанию с помощью Microsoft Excel. Отсортированная выборка представлена в таблице 1.

Таблица 1

Исходная выборка, отсортированная по возрастанию.

-2274,35	-414,16	-68,42	-38,05	-37,37	-35,15	-27,45	-20,9	-20,64	-20,42
-16,22	-14,69	-13,91	-11,87	-11,01	-10,98	-10,56	-10,22	-9,65	-9,29
-9,21	-8,89	-8	-7,38	-7,37	-7,37	-6,34	-6,28	-6,23	-5,97
-5,95	-5,09	-4,65	-4,56	-4,26	-4,13	-4,07	-3,95	-3,73	-3,42
-3,28	-3,1	-2,91	-2,68	-2,35	-1,81	-1,77	-1,6	-1,6	-1,45
-1,44	-1,42	-1,09	-1,07	-0,86	-0,85	-0,85	-0,81	-0,73	-0,68
-0,58	-0,42	-0,34	-0,25	-0,04	0	0,08	0,11	0,14	0,17
0,28	0,95	0,97	1,03	1,16	1,21	1,5	1,51	1,52	1,65
1,68	1,86	2,69	3,16	3,4	3,63	4,08	4,16	4,67	5,13
5,14	5,71	5,82	6,47	6,6	7,11	7,15	9,75	10,09	10,28
11,65	12,48	12,72	13,29	16,56	17,65	17,77	19,77	19,92	21,2
22,2	22,44	22,56	29,58	30,3	32,23	38,52	43,2	52,58	100,82

2. Разобьем весь диапазон наблюдаемых значений на интервалы. Рассчитаем количество интервалов по следующей формуле:

Так как , то

3. Определим размах выборки Для данной выборки (см. таблицу 1) , , тогда:

4. Находим ширину интервалов (шаг) по формуле:

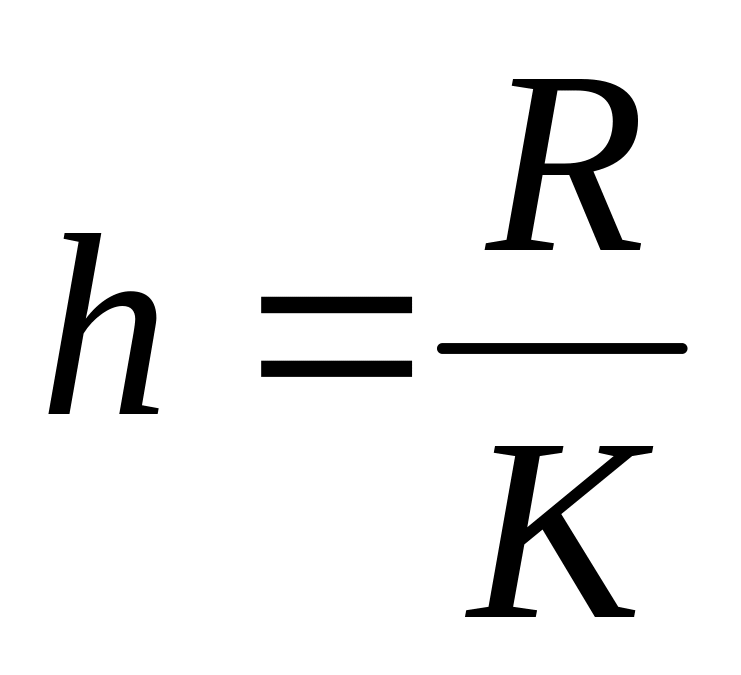
Так как , , то

5. Границы интервалов найдем по формулам:

6. Находим количество точек, попавших в i-ый интервал - частоты

7. Находим середину i-ого интервала .

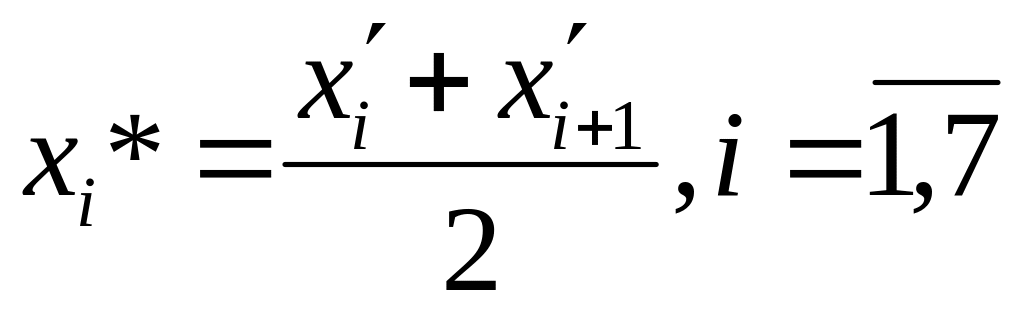8. Для каждого интервала находим накопленные частоты:

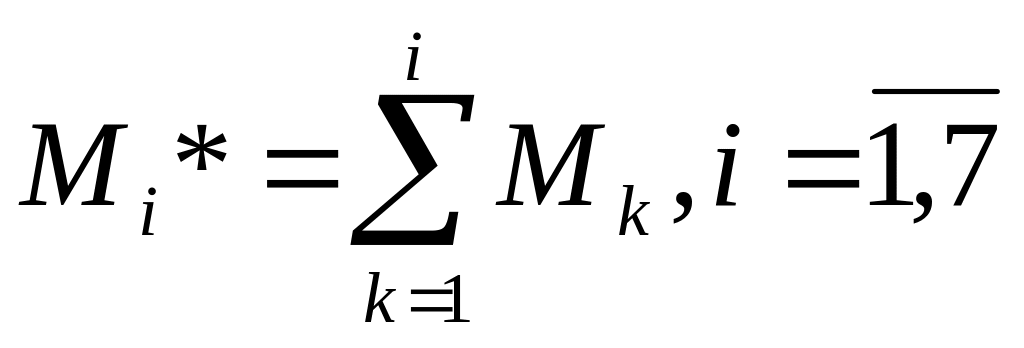
9. Определим относительную частоту i-ого интервала 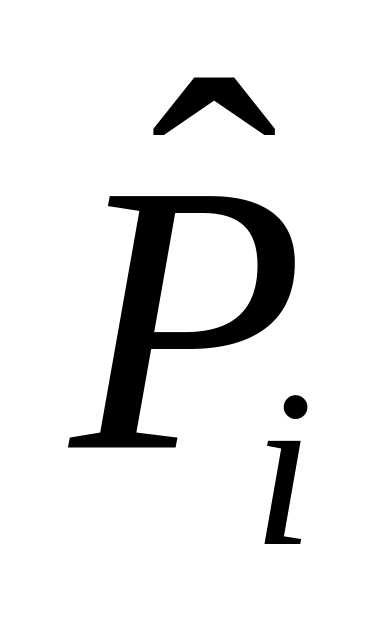по формуле:

10. Для каждого интервала находим относительные накопленные частоты по следующей формуле:

11. Для i-ого интервала находим оценку плотности вероятности:

Результаты расчетов приведены в таблице 2.

Таблица 2

Результаты расчетов для построения ЭФР, гистограммы и полигона частот

№
1	[-2274,35; -1935,04)	1	-2104,695	1	0,0083	0,0083
2	[-1935,04; -1595,73)	0	-1765,385	1	0	0,0083	0
3	[-1595,73; -1256,42)	0	-1426,075	1	0	0,0083	0
4	[-1256,42; -917,11)	0	-1086,765	1	0	0,0083	0
5	[-917,11; -577,8)	0	-747,455	1	0	0,0083	0
6	[-577,8; -238,49)	1	-408,145	2	0,0083	0,0166
7	[-238,49; 100,82]	118	-68,835	120	0,9833	0,9999

Графиком эмпирической функции распределения (ЭФР) случайной величины является ступенчатая функция. График полученной ЭФР показан на рис. 1.

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии . Гистограмма частот для данной выборки изображена на рис. 2.

Для построения полигона частот на оси абсцисс откладывают варианты , а на оси ординат – соответствующие им частоты . Точки соединяют отрезками прямых и получают полигон частот. Полигон частот заданной выборки показан на рис. 3.