Задание № 6.
61 |
Монета подброшена 3 раза. Написать закон распределения с. в. X— числа выпадений герба. Найти М (Х), D(Х). |
62 |
В урне 5 белых шаров и 3 красных. Из урны извлекают 2 шара. Найти закон распределения с. в. X— числа извлеченных красных шаров, а также М (Х), D(Х). |
63 |
Три стрелка производят по одному выстрелу в цель. Вероятность попадания для первого стрелка равна 0.5, для второго— 0.7, для третьего — 0.8. Найти закон распределения с. в. X — числа попаданий в цель, М (Х), D(Х). |
64 |
Прибор
состоит из трех независимо работающих
узлов. Вероятность отказа каждого
узла равна |
65 |
В партии из 7 деталей имеются 5 стандартных. Найти закон распределения с. в. X,равной числу нестандартных деталей среди трех отобранных, М (Х), D(Х). |
66 |
Имеются три станка, причем вероятность безотказной работы первого равна 0.9, второго — 0.7, третьего — 0.8. Найти закон распределения с. в. X— числа работающих станков, М (Х), D(Х). |
67 |
Производится три выстрела со следующими вероятностями попадания в цель: 0,3; 0,4; 0,7. Найти закон распределения с.в. Х, равной числу попаданий в цель. Вычислить М (Х), D(Х). |
68 |
В партии из 10 деталей 3 нестандартных. Наудачу отобраны 3 детали. Найти закон распределения и числовые характеристики с.в. Х, равной числу нестандартных деталей среди трех отобранных. |
69 |
Пусть с.в. Х равна числу выпавших нечетных цифр при однократном бросании четырех игральных кубиков. Найти закон распределения и числовые характеристики Х. |
70 |
На заводе три автоматических линии. Вероятность того, что в течение смены первая линия не потребует регулировки, равна 0,9, вторая – 0,8, третья – 0,7. Найти закон распределения и числовые характеристики с.в. Х, равной числу линий, не потребовавших регулировки. |
.
Найти закон распределения с. в. X—
числа отказавших узлов, М (Х), D(Х).
Задание № 7.
В задании 7 необходимо выполнить следующее:
В заданной функции f(x) найти параметр с, при котором f(x) является плотностью распределения случайной величины Х.
Найти функцию распределения F(x)
Построить графики f(x) и F(x)
Математическое ожидание, дисперсию и среднее квадратическое отклонение с.в. Х.
Вероятность попадания х в указанный интервал [a ; b]
71 |
f(x)
= |
76 |
f(x)
= |
72 |
f(x)
= |
77 |
f(x)
= |
73 |
f(x)
= |
78 |
f(x)
= |
74 |
f(x)
= |
79 |
f(x)
= |
75 |
f(x)
= |
80 |
f(x)
= |
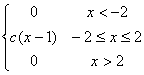a
= 1, b =3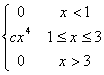
a
= 2, b =4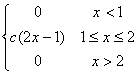
a
= 0, b =3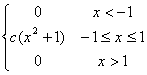
a
= -2, b =0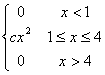
a
= 3, b =5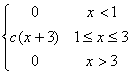
a
= 2, b =4
a
= 0, b =4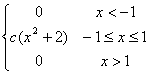
a
= -2, b =0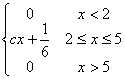
a
= 3, b =6
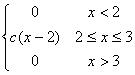a
= 2,5, b =3,5