2.3 Порядок выполнения работы

По заданной выборке наблюдений требуется построить в системе координат XOY диаграмму рассеяния, а по виду построенной диаграммы подобрать эмпирическую функцию и рассчитать параметры аппроксимирующей зависимости, применяя МНК.

Вычисления следует сводить в табл. 2.2, которая для подбора параметров линейной эмпирической зависимости может иметь вид:

Таблица 2.2

i	xi	yi	xi2	yi2	xi· yi
…	…	…	…	…	…

Данные последней строки табл. 2.2 подставляются в нормальную систему уравнений, решением которой находят значения параметров эмпирической функции.

Средние арифметические определяются по формулам:

и .

Корреляционный момент – ;

среднеквадратические отклонения –

; ;

выборочный коэффициент корреляции – ;

среднеквадратическое отклонение коэффициента корреляции – ;

надежность коэффициента корреляции – .

2.4 Пример выполнения задания

Опытные данные о значениях взаимозависимых величин представлены в таблице:

X	1	2	3	4	5	6
Y	15	10	2	2	-4	-10

По выборке наблюдений построим диаграмму рассеяния:

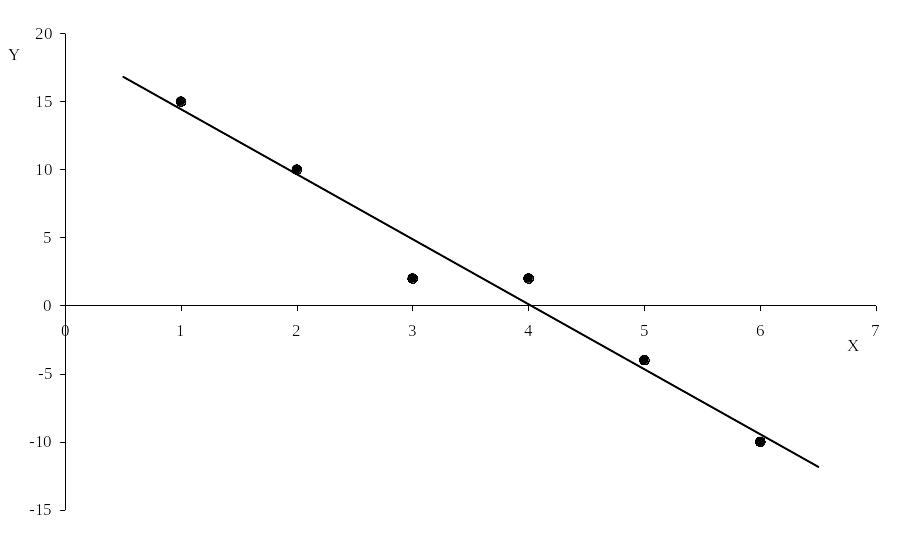
Анализ опытных данных показывает, что в качестве эмпирической функции можно использовать линейную зависимость y = a·x + b.

В выражении необходимо найти параметры a и b, для чего применяем МНК. Для удобства вычислений составляем расчетную таблицу:

i	xi	yi	xi2	yi2	xi· yi
1	1	15	1	225	15
2	2	10	4	100	20
3	3	2	9	4	6
4	4	2	16	4	8
5	5	–4	25	16	–20
6	6	–10	36	100	–60

Подставляем данные последней строки таблицы в нормальную систему уравнений:

Решая эту систему, получим a = – 4,76; b = 19,2.

То есть эмпирическая функция имеет вид y = – 4,76·x + 19,2.

Определяем средние арифметические выборки:

; .

Вычисляем корреляционный момент , из чего следует, что переменные связаны отрицательной корреляцией.

Определяем среднеквадратические отклонения:

; .

Вычисляем выборочный коэффициент корреляции:

.

Проверим значимость коэффициента корреляции: , что больше критического значения, равного 1,90 при уровне надежности 0,95 и числе измерений, равном 6 (табл. А. 3). Следовательно коэффициент корреляции надежен.

Среднеквадратическое отклонение коэффициента корреляции:

.

Надежность коэффициента корреляции:

.