Лабораторная работа №2

Подбор эмпирических зависимостей двух случайных величин методом наименьших квадратов

2.1 Цель занятия

В рамках данного занятия, которое рассчитано на 4 часа, производится обработка результатов испытаний горной породы на прочность до и после ее увлажнения.

Цель занятия состоит в формировании у студентов навыков исследования закономерностей случайных явлений или процессов, которые зависят от двух факторов.

Расчеты следует выполнять в соответствии с [2, 3], используя теоретические знания, полученные в курсе «Высшая математика». Для повторения материала, необходимо прочитать следующий раздел.

2.2 Элементы теории корреляции

Теория корреляции – это ветвь математической статистки, изучающая взаимосвязь между факторами и признаками при массовом наблюдении изменения средней величины одного из факторов в зависимости от значений другого.

Обозначим через (X,Y) двумерную случайную величину, где X и Y – компоненты или составляющие. Обе величины X и Y, рассматриваемые одновременно, образуют систему двух случайных величин. При изучении системы случайных величин недостаточно изучить в отдельности случайные величины, составляющие систему, надо учитывать еще и связи или зависимости между ними.

Законом распределения двумерной величины называют перечень возможных значений этой величины (т.е. пар чисел (х_i, у_i) и их вероятностей р_ij. Обычно это таблица с двойным входом, которая еще называется матрицей распределения. Она имеет вид:

Таблица 2.1

	хi	х1	…	хi	…	хn
уj
у1		р11		рi1		рn1
…
yj		р1j		рij		рnj
…
уm		р1m		рim		рnm

Чтобы найти вероятность того, что отдельная случайная величина, входящая в систему, примет определенное значение, надо просуммировать вероятности p_ij, стоящие в соответствующей этому значению строке (столбце) матрицы распределения.

Пусть задана двумерная дискретная случайная величина (X, Y) с возможными значениями x₁, x₂, … , x_n; y₁, y₂, … , y_m. Тогда условным распределением составляющей X при Y = у_t называется совокупность условных вероятностей: P(x₁/y_j), P(x₂/y_j), … , P(x_n/y_j). В общем случае условный закон распределения составляющей X: .

Аналогично находят условный закон распределения составляющей Y: .

Условным математическим ожиданием дискретной случайной величины Y при X = x_i, где x_i – определенное возможное значение случайной величины X, называется произведение возможных значений Y на их условные вероятности:

.

Условное математическое ожидание есть функция X, т.е. M(Y/X) = f(x), называемая функцией регрессии Y на X, а ее график – линией регрессии. Аналогично получают функцию регрессии X на Y:

.

Корреляционным моментом или ковариацией K_xy случайных величин X и Y называется математическое ожидание произведения их отклонений.

K_xy = M[(X – M(X))(Y – M(Y))] = M(X·Y) – M(X)·M(Y).

Для дискретных случайных величин его вычисляют по формуле:

.

Корреляционный момент служит для оценки связи между X и Y. Если случайные величины X и Y независимы, то корреляционный момент равен нулю (X и Y некоррелированные). Однако из некоррелированности еще не следует независимость. Если корреляционный момент равен нулю, то это означает только отсутствие линейной связи между X и Y, любой другой вид связи может присутствовать.

Коэффициент корреляции вычисляется по формуле:

,

где _x, _y – соответственно средние квадратические отклонения X и Y.

Величина r_xy характеризует степень линейной зависимости случайных величин X и Y. Эта зависимость проявляется в том, что при возрастании одной случайной величины другая имеет тенденцию также возрастать (или убывать). В первом случае r_xy > 0 и говорят, что случайные величины X и Y связаны положительной корреляцией. В случае же, когда r_xy < 0, X и Y связаны отрицательной корреляцией. Абсолютная величина коэффициента корреляции не превышает единицы, т.е. –1 ≤ r_xy ≤ 1.

Модуль |r_xy| коэффициента корреляции характеризует степень тесноты линейной зависимости между случайными величинами X и Y.

Для оценок условных математических ожиданий M(Y/X = x_i) или M(X/Y = y_j) принимают на практике условные средние, которые находят по данным опыта как средние арифметические наблюдаемых значений.

Тогда формула для корреляционного момента принимает вид:

.

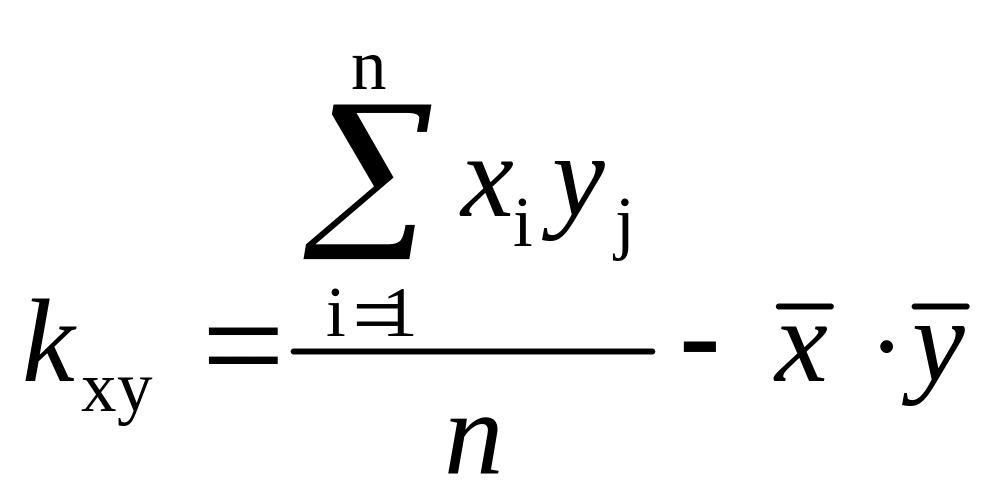Средние квадратические отклонения случайных величин X и Y рассчитывают по формулам:

; .

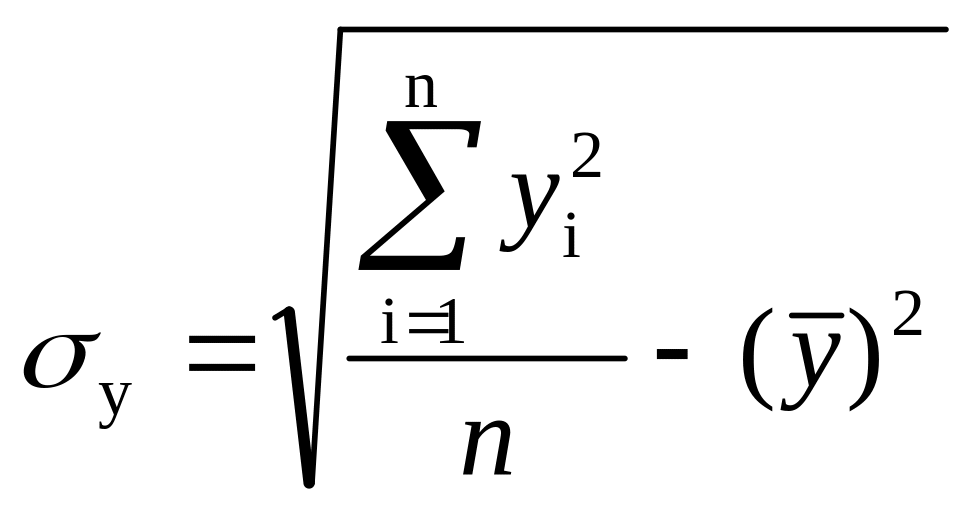Выборочный коэффициент корреляции, характеризующий тесноту связи между случайными величинами X и Y, определяется по формуле:

.

Надежность коэффициента корреляции определяют по формуле:

,

где _r – среднеквадратическое отклонение коэффициента корреляции, которое вычисляется по формуле:

.

Значимость коэффициента корреляции проверяется путем сравнения его абсолютной величины, умноженной на , с его критическим значением при заданной надежности P. Критические значения произведения для различных значений надежности P и различных чисел измерений n даны в табл. А.3

Выборочное уравнение регрессии должно быть таким, чтобы рассеяние опытных точек (x_i; y_i) было минимальным. Это означает, что отклонения фактических значений функции от «подобранного» уравнения z_i = y_i – должны быть минимальными, т.е. уравнение подбирается так, чтобы сумма квадратов отклонений была наименьшей:

z₁² + z₂² + … + z_i² + … + z_n² → min.

Метод, применяемый для решения подобной задачи, получил название метод наименьших квадратов (МНК). Этот метод не решает вопроса о выборе вида аналитической функции, он только позволяет определить наиболее вероятные значения параметров аппроксимирующей функции.

Предположим, что зависимость между случайными величинами может быть описана линейной функцией вида:

y = a·x + b.

Тогда, согласно МНК, должно выполняться равенство:

.

Требуется определить параметры a и b так, чтобы z достигла минимума. Известно, что необходимое условие существования минимума состоит в том, чтобы

; .

После дифференцирования получается система уравнений:

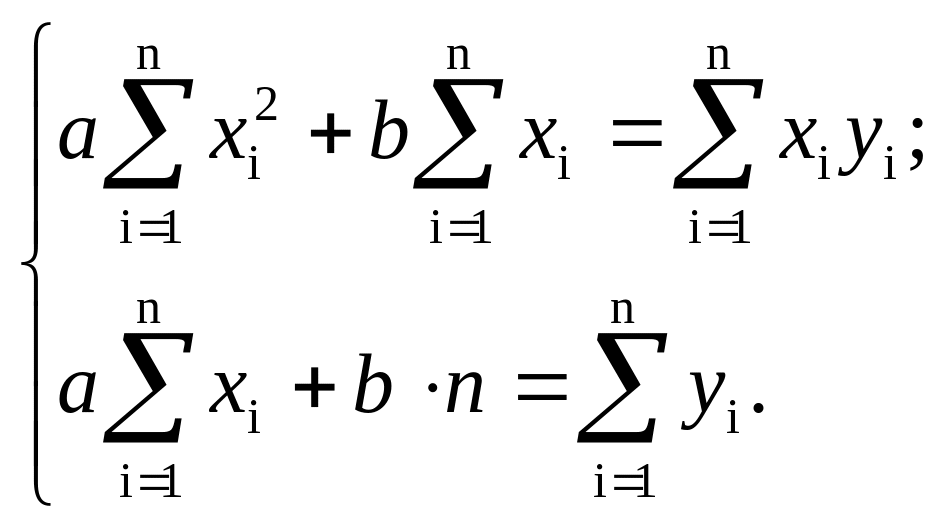
Полученная система называется системой нормальных уравнений в случае выбора эмпирической функции в виде линейной зависимости.

Если эмпирическую зависимость целесообразно выбрать в виде квадратичной функции

y = a·x² + b·x + c,

тогда, согласно МНК, параметры уравнения могут быть определены решением следующей системы нормальных уравнений:

Для гиперболической функции вида:

Система нормальных уравнений, согласно МНК, приобретает вид: