1.4 Пример выполнения задания
Производительность одного забойщика (т/смену) составила:
18,1 |
19,3 |
20,1 |
20,8 |
21,5 |
22,5 |
22,9 |
23,3 |
24,2 |
25,0 |
18,2 |
19,5 |
20,2 |
20,9 |
21,5 |
22,5 |
22,9 |
23,5 |
24,3 |
25,0 |
18,3 |
19,5 |
20,3 |
21,0 |
21,5 |
22,5 |
22,9 |
23,5 |
24,4 |
25,3 |
18,4 |
19,6 |
20,6 |
21,0 |
21,7 |
22,5 |
23,0 |
23,6 |
24,4 |
25,7 |
18,4 |
19,6 |
20,6 |
21,2 |
21,7 |
22,6 |
23,0 |
23,7 |
24,5 |
25,7 |
18,5 |
19,7 |
20,7 |
21,2 |
21,8 |
22,6 |
23,0 |
23,8 |
24,5 |
26,0 |
19,0 |
19,7 |
20,7 |
21,3 |
21,9 |
22,7 |
23,1 |
23,8 |
24,7 |
26,1 |
19,1 |
19,9 |
20,8 |
21,3 |
22,0 |
22,7 |
23,2 |
23,9 |
24,7 |
26,3 |
19,2 |
19,9 |
20,8 |
21,4 |
22,2 |
22,7 |
23,2 |
23,9 |
24,8 |
26,7 |
19,2 |
20,0 |
20,8 |
21,5 |
22,2 |
22,7 |
23,2 |
24,2 |
24,9 |
26,8 |
Минимальное значение Xmin = 18,1.
Максимальное значение Xmax = 26,8.
Длина интервала по
формуле Стэрджеса:
.
Начало первого
интервала:
.
Далее заполняем расчетную таблицу:
№ п/п |
Границы интервалов |
Середина интервала, xi |
Частота, ni |
Относительная частота, wi |
Накопленная частота, Nni |
Накопленная относительная частота, Nwi |
|
i |
i+1 |
||||||
1 |
18 |
19 |
18,5 |
6 |
0,06 |
6 |
0,06 |
2 |
19 |
20 |
19,5 |
13 |
0,13 |
19 |
0,19 |
3 |
20 |
21 |
20,5 |
13 |
0,13 |
32 |
0,32 |
4 |
21 |
22 |
21,5 |
15 |
0,15 |
47 |
0,47 |
5 |
22 |
23 |
22,5 |
16 |
0,16 |
63 |
0,63 |
6 |
23 |
24 |
23,5 |
16 |
0,16 |
79 |
0,79 |
7 |
24 |
25 |
24,5 |
11 |
0,11 |
90 |
0,90 |
8 |
25 |
26 |
25,5 |
5 |
0,05 |
95 |
0,95 |
9 |
26 |
27 |
26,5 |
5 |
0,05 |
100 |
1,00 |
Для расчета характеристик выборки используем метод условного нуля.
xi |
ni |
ui |
ni·ui |
ni·ui2 |
ni·(ui + 1)2 |
Условные моменты |
|
M1* |
M2* |
||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
18,5 |
6 |
-4 |
-24 |
96 |
54 |
|
|
19,5 |
13 |
-3 |
-39 |
117 |
52 |
||
20,5 |
13 |
-2 |
-26 |
52 |
13 |
||
21,5 |
15 |
-1 |
-15 |
15 |
0 |
||
22,5 |
16 |
0 |
0 |
0 |
16 |
||
23,5 |
16 |
1 |
16 |
16 |
64 |
||
24,5 |
11 |
2 |
22 |
44 |
99 |
||
25,5 |
5 |
3 |
15 |
45 |
80 |
||
26,5 |
5 |
4 |
20 |
80 |
125 |
||
|
|
= |
-31 |
465 |
503 |
-0,31 |
4,65 |
Проверка 503 = 465 + 2·(-31) + 100 = 503.
Среднее арифметическое: 
;
Дисперсия: 
;
Среднее квадратическое
отклонение: 
;
Коэффициент
вариации: 
.
Для определения асимметрии и эксцесса вычислим центральные моменты третьего и четвертого порядков:
xi |
ni |
|
|
|
|
|
Центральные моменты |
|
M3 |
M4 |
|||||||
18,5 |
6 |
-3,69 |
-50,243 |
185,398 |
-301,458 |
1112,388 |
|
|
19,5 |
13 |
-2,69 |
-19,465 |
52,361 |
-253,045 |
680,693 |
||
20,5 |
13 |
-1,69 |
-4,827 |
8,157 |
-62,751 |
106,041 |
||
21,5 |
15 |
-0,69 |
-0,329 |
0,227 |
-4,935 |
3,405 |
||
22,5 |
16 |
0,31 |
0,030 |
0,009 |
0,480 |
0,144 |
||
23,5 |
16 |
1,31 |
2,248 |
2,945 |
35,968 |
47,120 |
||
24,5 |
11 |
2,31 |
12,326 |
28,474 |
135,586 |
313,214 |
||
25,5 |
5 |
3,31 |
36,265 |
120,036 |
181,325 |
600,180 |
||
26,5 |
5 |
4,31 |
80,063 |
345,071 |
400,315 |
1725,355 |
||
|
|
|
|
= |
131,485 |
4588,540 |
1,31 |
45,89 |
Асимметрия: 
.
Эксцесс: 
.
Построим гистограмму:
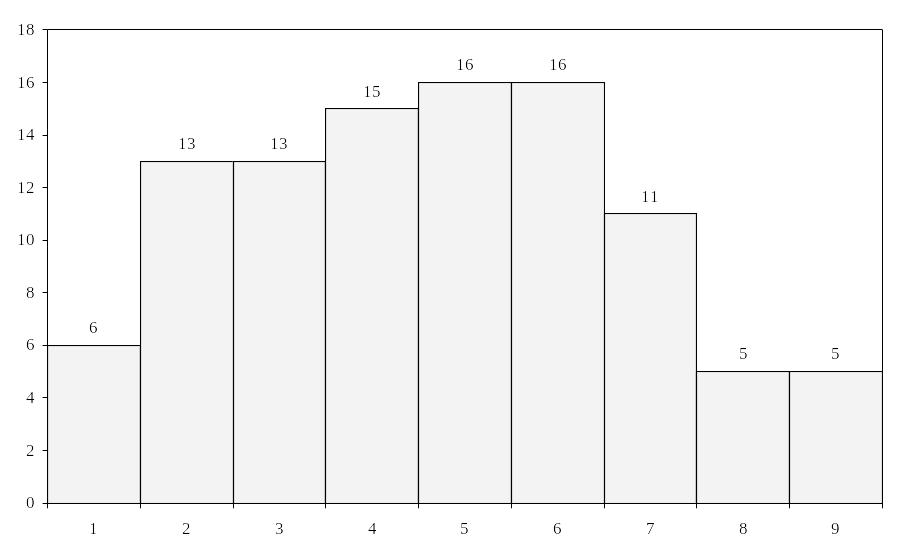
По виду гистограммы и вычисленным значениям асимметрии и эксцесса принимаем гипотезу, что случайная величина подчиняется нормальному закону распределения.
Рассчитаем критерий 2‑Пирсона:
i |
xi |
zi |
(zi) |
|
ni |
ni– n′i |
(ni– n′i)2 |
|
1 |
18,5 |
-1,732 |
0,089 |
4,178 |
6 |
1,822 |
3,320 |
0,795 |
2 |
19,5 |
-1,263 |
0,180 |
8,451 |
13 |
4,549 |
20,693 |
2,449 |
3 |
20,5 |
-0,793 |
0,291 |
13,662 |
13 |
-0,662 |
0,438 |
0,032 |
4 |
21,5 |
-0,324 |
0,379 |
17,793 |
15 |
-2,793 |
7,801 |
0,438 |
5 |
22,5 |
0,146 |
0,395 |
18,545 |
16 |
-2,545 |
6,477 |
0,349 |
6 |
23,5 |
0,615 |
0,330 |
15,493 |
16 |
0,507 |
0,257 |
0,017 |
7 |
24,5 |
1,085 |
0,221 |
10,376 |
11 |
0,624 |
0,389 |
0,037 |
8 |
25,5 |
1,554 |
0,119 |
5,587 |
5 |
-0,587 |
0,345 |
0,062 |
9 |
26,5 |
2,023 |
0,052 |
2,441 |
5 |
2,559 |
6,548 |
2,683 |
|
|
|
|
|
|
|
набл.2= |
6,862 |
Критическое значение кр2 при уровне значимости = 0,05 и количестве степеней свободы k = 9 – 1 – 2 = 6 составляет 12,592 > 6,862. Таким образом, нет оснований отвергать принятую гипотезу о нормальном распределении статистической совокупности.