1.4.2. Классификация измерительных преобразователей

Исходя из определения ИП, как четырехполюсника, классификацию ИП целесообразно приводить по роду входных величин, подлежащих измерению, или по выходным величинам, присущим самому принципу действия преобразователя. Например, ИП давления или резистивные ИП, ИП температуры или термоэлектрические ИП и т. п. Более объединяющим является энергетический признак связи между входными и выходными величинами – это “пассивные” и “активные” ИП или параметрические и генераторные ИП. Принципиальное отличие заключается в том, что “пассивные” ИП требуют внешних источников питания, а генераторные сами являются источниками ЭДС Классификация ИП по принципу действия дает наилучший эффект с точки зрения изучения ИП.

Рассмотрим сначала наиболее распространенные входные величины и их производные, которые определяют тип преобразователя по виду входной величины. Линейное перемещение (длина, толщина, уровень, качество поверхности, эрозия, износ, вибрация, деформация). Угловое перемещение (угловая вибрация, направление потока, угол атаки). Линейная и угловая скорость (расход, вибрация, количество движения, скорость вращения). Сила (вес, удельный вес, напор, механическое напряжение, вращающий момент, давление, поток, высота). Температура (теплопроводность и радиация, давление, скорость газа). Свет (световой поток и освещенность, спектральное распределение, длина волны, частота, число). Время (частота, число – счет, фаза, временной интервал).

Рассмотрим далее наиболее полезные физические явление, которые используются в ИП и которые классифицируют их по принципу действия.”Активные” (генераторные) типы преобразователей : электромагнитный, пьезоэлектрический, термоэлектрический, фотоэлектрический, электрокинетический. “Пассивные” (параметрические) типы преобразователей: резистивный, индуктивный, емкостный, магниторезистивный, терморезистивный, фоторезистивный, магнитоупругий, ионизационный.

Входные величины разделяются также на два класса: величины, характеризующие протекание процессов и величины, характеризующие свойства и состав вещества.

По естественной входной X и выходной Y величинам ИП классифицируются следующим образом: X_НЭ→Y_НЭ;X_НЭ→Y_ЭЛ;X_ЭЛ→Y_НЭ, (НЭ – неэлектрическая и ЭЛ – электрическая величины). Например, температура – высота ртутного столба; температура – термо-ЭДС; напряжение – угол отклонения подвижной части.

Выходные сигналы классифицируются сложно, но можно выделить наиболее распространенные виды: аналоговые, модуляционные и кодовые. Как правило, выходной сигнал является модулированным, т.е. на несущий выходной сигнал (ток, напряжение, частота, давление воздуха и т.д.) воздействует информативный входной сигнал, изменяя его амплитуду, частоту, фазу и другие параметры.

1.4.3. Основные характеристики и параметры ип

Применительно к ИП под характеристикой будем понимать в широком смысле зависимость между выходной и входной величинами. Параметры физической величины – это вспомогательные характеристики этой величины. Например, при измерении электрического напряжения переменного тока частоту рассматривают как параметр напряжения.

Подлежащая измерению величина, воздействующая на ИП может иметь статический (квазистатический) или динамический характер. Эти группы величин определяют статические и динамические характеристики ИП. Рассмотрим их подробнее.

Наиболее информативной является номинальная статическая характеристика (НСХ), которая выражает функциональную зависимость между выходной и входной величинами y=f(x). НСХ не зависит от времени. Она может задаваться аналитически, графически или ввиде таблиц. Аналитическое представление используется при теоретических исследованиях, графическое, как правило, для визуального анализа, таблицы используют при расчетах. Обычно НСХ дается ввиде уравнения:

y=(a₀+a₁x+a₂x²+a₃x³+…+a_nxⁿ)x,

где x и y соответственно входная и выходная величины; а₀, а₁, а₂, а₃, …а_n – градуированные коэффициенты. В общем случае градуированная кривая может быть представлена некоторой линией, примыкающей к прямой а₀x. В графическом виде они представлены на рисунке 1.1 (а, б, в, г).

+y +y

	-x +x -x 9.15 Схема электрокинетического преобразователя Рисунок 9.14 Схема для измерения давления с помощью ионистра γ Е Р Р Рисунок 9.14 Схема для измерения давления с помощью ионистра γ Рисунок 9.13 Схема устройства ионистра JJ Pt Pt Рисунок 9.12 График, поясняющий работу полярографического преобразователя Zn Sn Fe 0 l J Рисунок 9.11 Схема полярографического преобразователя Hg Hg K A Рисунок 9.10 Схема кулонометрического преобразователя Э1 HgJ K A Э2 J= 0 1 2 3 10 Рисунок 9.9 Схема гальванического преобразователя со стеклянным электродом Е­ =рН НР К КЭ Рисунок 9.8 Конструкция стеклянного электрода рН - метра НР К Э Рисунок 9.7 Схема гальванического преобразователя с водородным электродом Pt Н2 Н2 Рисунок 9.3 Схема, объясняющая образование потенциала течения Q V Э1 Э2 ПП Рисунок 9.2 Схема электрохимического преобразователя Р2 Р1 + - ПП °C 0 NaOH HCl γ Рисунок 9.1 Зависимость проводимости электролитов от температуры -x +x
-y

-y

а)y=a₀x б) y=a₀x+a₁x²+a₃x⁴+…

+y +y

-x +x -x +x

-y -y

в)y=a₀x+a₂x³+a₄x⁵+… г)y=a₀x+a₁x²+a₂x³+…

Рисунок 1.1. Статические характеристики ИП

Предпочтительными являются кривые, описываемые уравнениями с нечетными степенями а₀х, а₀х+х³, и т.д. При этом достигается достаточно хорошая линейность при значительных отклонениях от нуля.

Уравнение измерительного преобразователя – это зависимость между информативными параметрами выходного и входного сигналов

y=f(x; a₁,a₂,a₃,…a_n; b₁,b₂,b₃,…b_m; E₁,E₂,E₃,…E_k),

где а_i – неинформативные параметры входного сигнала; b_i – параметры измерительного преобразователя;E_i – влияющие величины.

Отношение К_п=у/х – называется коэффициентом преобразования.

Вследствие воздействия на ИП различных факторов градуировочная характеристика ИП оказывается неоднозначной и из линии превращается в полосу неопределенности. Половина полосы неопределенности Δ₀ есть абсолютная погрешность. Распределение полосы может иметь двоякий характер. Ширина может оставаться постоянной вдоль всей НСХ. В этом случае погрешность называется погрешностью нуля или аддитивной погрешностью. В другом случае ширина полосы неопределенности оказывается возрастающей пропорционально текущему значению х. Такая погрешность называется погрешностью от изменения чувствительности или мультипликативная погрешность. Для этих случаев абсолютная погрешность определяется, как 2Δ₀ и 2γ_Sх соответственно. В большинстве реальных ИП обе погрешности присутствуют одновременно. Изменение текущей погрешности вдоль изменения х аппроксимируется в этом случае двучленным полиномом Δ=Δ₀+γ_Sx, где х – текущее значение измеряемой величины; γ_S – относительная погрешность от изменения чувствительности ИП; Δ₀ – абсолютное значение погрешности от смещения нуля. Относительная погрешность определяется по формуле γ=Δ/x=γ_S+Δ₀/x. Графики изменения абсолютной и относительной погрешности приведены на рисунке.

Δ γ=Δ/x

γ_Sx

Δ₀/x

Δ₀ γ_S

0 x x

Рисунок 1.2. Зависимость погрешности от изменения входной величины

Важными статическими характеристиками ИП являются разрешающая способность и чувствительность.

Чувствительность – это предел отношения приращения выходной величины ИП к приращению входной (рисунок 1.3):

, при → 0.

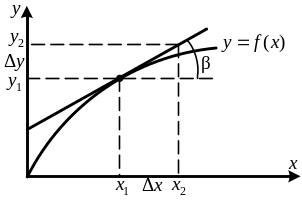
Рисунок 1.3. Определение чувствительности преобразователя

При линейной функции чувствительность преобразователя определяется как отношение выходной величины к входной и остается постоянной.

Разрешающая способность – это числовая характеристика, оценивающая способность ИП к обнаружению малых изменений входной величины в любой части диапазона преобразования. Ее выражают как абсолютной, так и относительной величиной. Абсолютная разрешающая способность совпадает с понятием порога чувствительности, под которым понимается величина, равная абсолютной величине погрешности нуля Δ₀.

Относительная разрешающая способность является более важной характеристикой. При информационном подходе разрешающую способность ИП следует определять, как число достоверно различимых градаций во всем диапазоне преобразования и выражать числом больше единицы. Это понятие сформулировано Ф.Е.Темниковым “… надежное квантование при любом распределении погрешности прибора по его диапазону определяется в каждом участке диапазона текущей шириной d=2Δ полосы ошибок, и в качестве квантов измеряемой величины должны рассматриваться ступени, вписывающиеся в полосу ошибок по всей ее длине”. Таким образом, разрешающая способность представляется как совокупный показатель текущей точности и длины диапазона ИП.

Текущий размер отдельной ступени разрешающей способности (R_рс) определяется текущей шириной полосы погрешностей, т.е. равен 2Δ текущей погрешности ИП. Поэтому в полосе значений преобразуемой величины шириной dx указывается dx/2Δ ступеней. Отсюда полное число ступеней, т.е. R_рс в диапазоне от х₁ до х₂ определяется выражением R_рс= , где Δ – текущее значение погрешности, определяемое одно или двухчленной формулой. На основании соотношений 2Δ=2γ_x=x/A получим:

R_рс= ,

где А=1/γ – точность преобразования.

Полученное выражение показывает, что R_рс есть площадь, заключенная под кривой логарифмической характеристикой точности (ЛХТ) в границах рассматриваемого диапазона.

Действительно, обозначая х=е^у и у=lnx, получим:

R_СТ= .

Графически ЛХТ имеет вид представленный на рисунке 1.4:

А =1/2γ_S

₁

2

lnx

0 lnΔ₀ lnx₁ lnx₂ lnx_m

Рисунок 1.4. Логарифмическая характеристика точности ИП

Из графика видно, что R_рс ИП есть обобщенная характеристика высоты и ширины ЛХТ.

Для ИП с чисто аддитивной погрешностью, т.е. Δ=Δ₀

R_ст=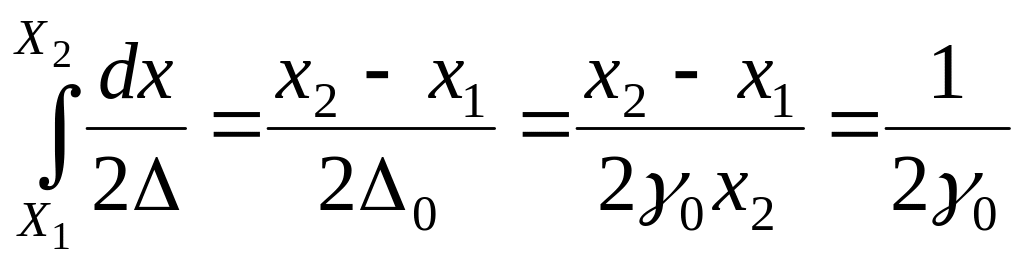 (1- )= .

Здесь D_р=х₂/х₁ – относительная величина рабочего диапазона. Это выражение соответствует участку 1 ЛХТ. Для этого же случая полный диапазон ИП D_p=1/γ₀ и тогда R_ст=1/2(D_p-1).

При чисто мультипликативной погрешности, когда по сравнению с х₁ можно положить γ₀=0, т.е. представить ширину полосы ввиде треугольника R_ст зависит не только от D_h, но и от γ_s, тогда:

R_ст=1/(2γ_s)ln =1/(2γ_s)lnD_p.

Это значение R_ст соответствует площади участка 2. В общем случае, при наличии γ_s и γ₀ разрешающая способность ИП определяется формулой:

R_ст=1/2 ,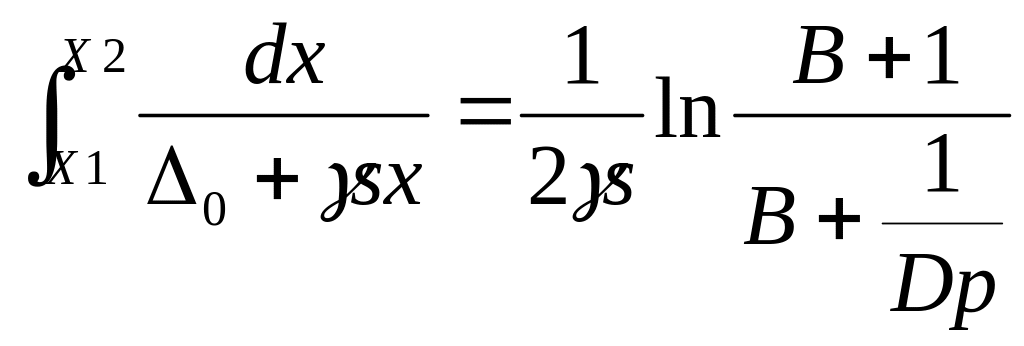

где B=γ₀/γ_s и D_p=х₂/х₁.

Динамические характеристики определяют поведение ИП при быстрых изменениях входной величины. Динамическая характеристика зависит от внутренней структуры ИП и его элементов. Она может быть задана методами:

1. динамическим оператором (передаточной функции), представляющим собой дифференциальное уравнение, связывающее входную и выходную величины, выраженные в операторной форме;

2. переходной характеристикой у=f(t), где t – время при скачкообразном изменении входной величины;

3. амплитудно-фазовой характеристикой – годографом вектора выходного сигнала, отнесенного к вектору входной величины при ее изменении по синусоидальному закону с частотой, изменяющейся от 0 до бесконечности;

4. амплитудно-частотной (АЧХ) и фазовой характеристиками.

Частотная характеристика – зависимость чувствительности ИП от частоты изменения входного сигнала. Фазовая характеристика – зависимость сдвига фаз между векторами входной и выходной величин в зависимости от синусоидального изменения входной величины.

В зависимости от динамических свойств ИП может быть отнесен к определенному типу динамических звеньев:

У=S∙x – идеальное;

У= – инерционное первого порядка;

У= – инерционное с запаздыванием;

У= – инерционное второго порядка;

У= – колебательное;

У= – интегрирующее;

У= – дифференцирующее идеальное;

У= – дифференцирующее реальное.

В приведенных формулах р – оператор Лапласа, T₁, T₂ – постоянные времени, S – чувствительность, t_s – время запаздывания.

Наиболее употребительными динамическими характеристиками являются: частотная характеристика, постоянная времени, время запаздывания и динамическая погрешность. Постоянная времени характеризует, время в течение которого после скачкообразного изменения входной величины, выходная достигает 63 % установившегося значения (время 37 %-ного недохода). Недоход в 1 % характеризует, например, полное время установления процесса с точностью до 1 %. Динамическую погрешность можно определить из выражения операторного уравнения ИП:

У(р)=S_n(р)[x(p)+Δx(p)],

где S_n(p), x(p), Δx(p) – операторные изображения чувствительности, входной величины и погрешности ИП, соответственно.

Динамическая погрешность Δх_g определяется по формуле:

Δx_g(t)=F_H^-1{L[S_n(p)x(p)+S_n(p)Δx(p)]}-x(t),

где F_H^-1 – символ функции, обратной НСХ ИП; L – символ обратного преобразования Лапласа.

В более удобной форме выражение для динамической погрешности имеет вид:

Δх_g(t)=1/S^-1_n(y(t)-x(t)).

На практике решаются две задачи: при заданном времени установления определяют динамическую погрешность и наоборот, по заданной погрешности определяют время установления. Например, для стрелочных измерительных приборов время установления равно 4 с. При этом динамическая погрешность не должна превышать основной погрешности.

Для определения погрешности ИП по виду частотной характеристики можно воспользоваться приближенными формулами:

γ_а≈-1/2(f/f_c)²; f_c=2π/τ для апериодического ИП;

γ_k≈(1-2β²)(f/f_c)² для колебательного ИП,

где f_c – частота среза АЧХ; τ – постоянная времени ИП; f₀ – собственная резонансная частота ИП; β – коэффициент успокоения (0,6 – 0,7).

Более полное выражение для частотной погрешности имеет вид:

γ_ω= ,

где η=ω/ω₀ – отношение текущего значения частоты к частоте собственных колебаний ИП. Для наиболее характерных режимов успокоения выражения для частотной погрешности имеет вид:

γ_ω= = ; при β = 0,

γ_ω= при β = 1,

γ_ω= , при β = 0,7.