1.2 Метод электромеханических аналогий

Исследование внутренней структуры преобразователей наиболее эффективно производится методом электрических аналогий [2]. Этот метод позволяет закончить уравнения движения данной механической системы соответствующими уравнениями для эквивалентной электрической цепи, что существенно упрощает задачу. В большинстве случаев задача сводится к исследованию некоторого эквивалентного колебательного контура, свойства которого всесторонне изучены в теории электрических цепей. “Единство природы обнаруживается в поразительной аналогичности дифференциальных уравнений, относящихся к разным областям явлений” (В.И.Ленин. Материализм и эмпириокритицизм.).

Рассмотрим пример электродинамических аналогий.

Уравнение для последовательного колебательного контура, находящегося под действием синусоидальной ЭДС

Ldi/dt+Ri+1/C =E_msint

или в размерностях заряда:

Ld²q/dt²+Rdq/dt+ q= E_msint,

где L, R, C – соответственно индуктивность, сопротивление и емкость контура.

В электромеханических преобразователях с одной степенью свободы (линейное или угловое перемещение) при наличии массы и пружины уравнение поступательного движения имеет вид:

Md²x/dt²+R_mdx/dt+ x=F_msint,

а для вращательного движения:

Jd²/dt+Pd/dt+ =D_msint ,

где J, P, – соответственно момент инерции системы, коэффициент успокоения, эластичность растяжек или пружин.

Приведенные уравнения аналогичны по форме, поэтому аналогичны и их решения. Модули полных сопротивлений находятся, как отношение действующей силы к возникающей вследствие этого скорости, т.е. сопротивления:

Z= ;

Z_Mx= ;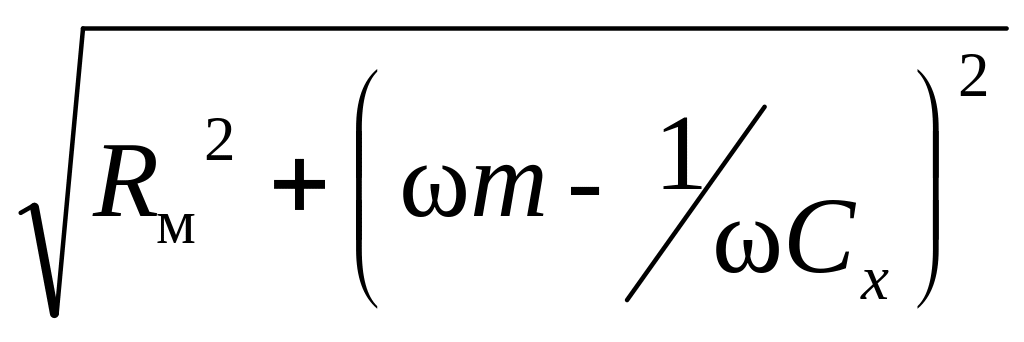

Z_M= ;

где Z, Z_Mx, Z_M – полные сопротивления электрической цепи и механической цепи при линейном и угловом перемещении,W=1/C_.

На практике установились следующие обобщенные силы, перемещения и скорости для различных видов энергии (таблица 1.1), и системы аналогий (таблица 1.2).

Таблица 1.1. Обобщенные силы, перемещения и скорости для различных видов энергии

Вид энергии	Обобщенные силы	Обобщенные перемещения	Обобщенные скорости
Электрическая Магнитная Механическая Тепловая Химическая	ЭДС (напряжение) Магнитодвижущая сила Сила Момент Давление Температура Химический потенциал	Количество электричества Магнитный поток Линейное перемещение Угловое перемещение Объем среды Энтропия Количество вещества	Ток ЭДС Линейная скорость Угловая скорость Объемная скорость Производная от энтропии по времени Скорость реакции

Таблица 1.2. Система аналогий механических и электрических величин

Механические величины	Электрические аналогии
Линейное перемещение х	Количество электричества q
Угловое перемещение 
Механическая скорость dx/dt,d/dt	Электрический ток I
Действующая сила F или момент D	Электродвижущая сила E
Сила реакции системы Fx, момент M	Напряжение U
Полное механическое сопротивление	Полное электрическое сопротивление
Механическое сопротивление потерь	Активное сопротивление R
Масса m, момент инерции J	Индуктивность L
Эластичность, гибкость пружины	Электрическая емкость C
Упругость, удельный противодействующий момент	Величина, обратная емкости, т.е.1/C

Существует и другая система аналогий, в которой электрическим аналогом механической силы служит ток, а скорости соответствует напряжение.