3. Емкостные преобразователи

В простейшем случае емкостные преобразователи представляют собой плоский конденсатор, состоящий из двух пластин с расстоянием δ, площадью S и диэлектрической проницаемостью среды ε (рисунок 3.1.).

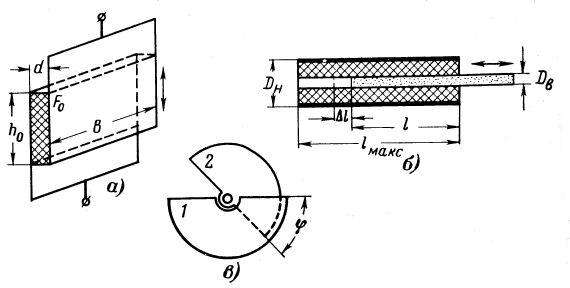
Рисунок 3.1. Ёмкостные преобразователи с изменяемой площадью:

а – плоский; б – цилиндрический; в – поворотный

Емкость плоского конденсатора определяется соотношением:

;

где S – действующая площадь обкладок, составляющих конденсатор; ε – относительная диэлектрическая проницаемость (для воздуха ε=1); ε₀ – электрическая постоянная, равная 8,85·10⁻¹² Ф/м; d – толщина диэлектрика (или расстояние между пластинами).

В зависимости от того, на какой параметр воздействует измеряемая величина, возможны следующие варианты:

, ε=const , d= const;

, F=const , d= const;

, F=const , ε = const;

Виды номинальных статических характеристик представлены на рисунке 3.2. Постоянство отмеченных параметров необходимо для уменьшения погрешности преобразования.

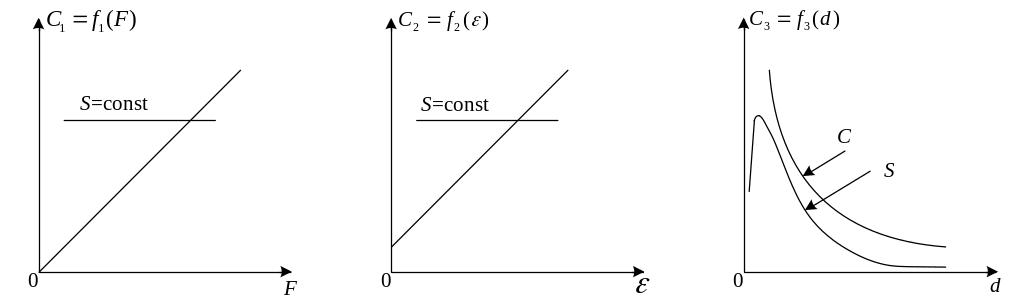Рисунок 3.2. Статические характеристики ёмкостных преобразователей

(S – чувствительность преобразователя)

Некоторые применения ёмкостных преобразователей представлены на рисунках 3.3. – 3.8 [10 ].

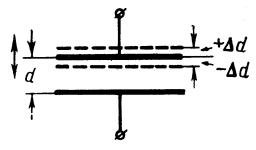
Рисунок 3.3. Ёмкостный преобразователь с изменением зазора

Абсолютное изменение ёмкости а относительное изменение .

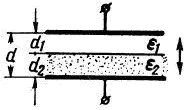
Рисунок 3.4. Преобразователь с переменной толщиной диэлектрика

а) б)

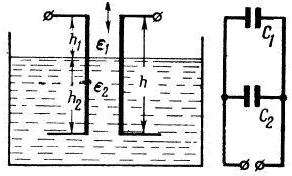
Рисунок 3.5. Ёмкостные преобразователи с переменным диэлектриком:

а) конструкция; б) эквивалентная схема

;

где b и h – линейные размеры пластин преобразователя.

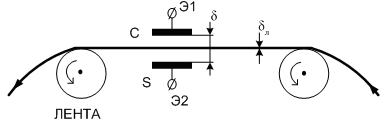
Рисунок 3.6. Изменение толщины диэлектрической ленты. δ – расстояние между пластинами, δ_л – толщина ленты, S – площадь пластин, ε₀ – диэлектрическая проницаемость среды, ε_л – диэлектрическая проницаемость ленты

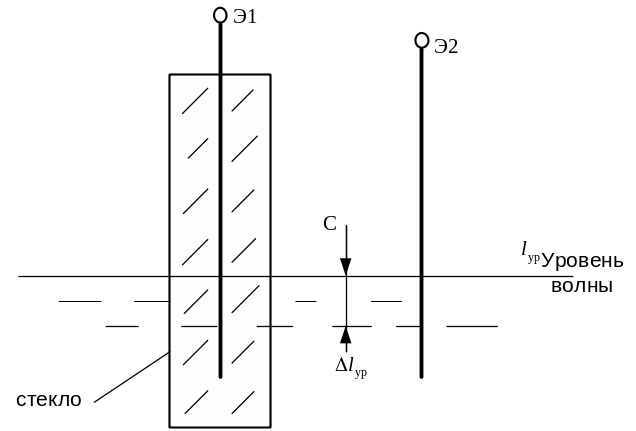
Рисунок 3.7. Изменение уровня волны

Емкость между электродами Э₁, Э₂ :

,

где R_1, R₂ – радиусы электродов; l_n – длина электродов.

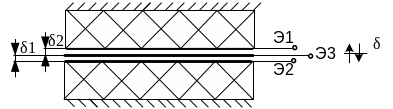
Рисунок 3.8. Дифференциальный емкостный преобразователь перемещения

Дифференциальный емкостный преобразователь специальной конструкции позволяет преобразовать перемещение от мм до мкм. Порог чувствительности составляет 10^-14 м.

Преимущество емкостных преобразователей:

– низкая нагрузка на объект исследования;

– отсутствие шумов, возможность компенсации температурной погрешности, простота конструкции.

К недостаткам следует отнести высокое внутреннее сопротивление и малую выходную мощность.

Возможные варианты измерительных схем с емкостными преобразователями представлены на рисунке 3.9.

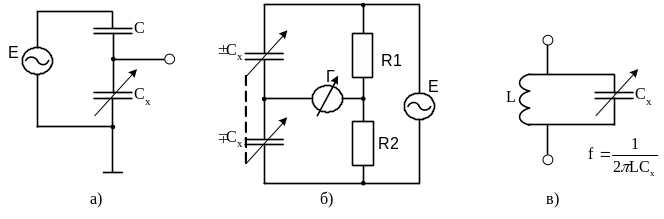Рисунок 3.9. Измерительные схемы с емкостными преобразователями: а – схема делителя; б – мостовая дифференциальная схема; в – схема с резонансным контуром

4. Индуктивные преобразователи

Принцип действия преобразователей основан на изменении индуктивности и комплексного сопротивления катушки под воздействием измеряемой неэлектрической величины.

В случае преобразования небольшого зазора δ.

,

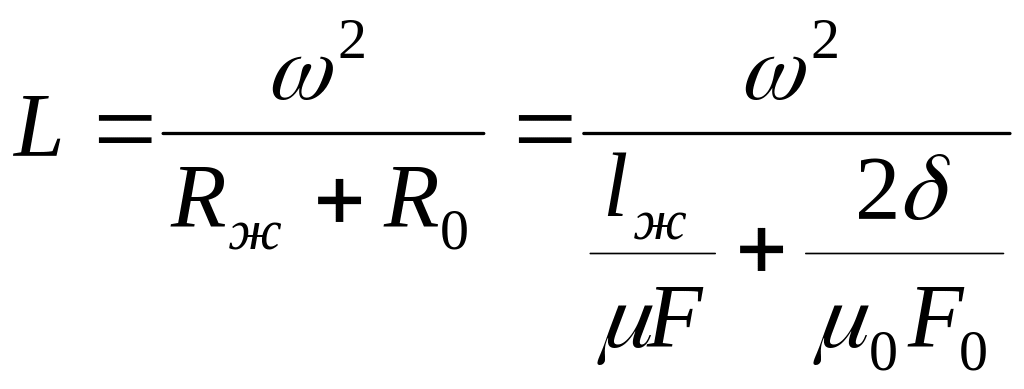где l_ж – средняя длина магнитной силовой линии в якоре и ярме; F, – площадь сечения якоря и воздушного зазора, δ – возникающие зазоры. В этой формуле не учитываются потери на вихревые токи и гистерезис, R_ж и R₀ – магнитное сопротивление сердечника и зазора; – число витков катушки.

В случае R_ж >> R₀ индуктивность определяется по формуле

.

Удовлетворительная линейность имеет место тогда, когда Δδ<<δ_заз:

.

Относительное изменение сопротивления Z и тока I будет тем больше, чем выше добротность катушки:

.

Чувствительность индуктивного преобразователя

,

а полное сопротивление его обмотки на частоте

,

где - активная составляющая сопротивления.

Ток в обмотке определяется по формуле

.

Рассмотрим схемы различных видов преобразователей.

На рисунке 4.1 представлен индуктивный дроссельный преобразователь.

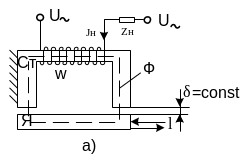
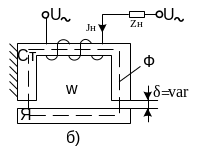
Рисунок 4.1. Индуктивные преобразователи: а – с переменной площадью зазора (пределы изменения l=0-20 мм). На схеме Ст – статор ; Я – якорь; Zн – сопротивление нагрузки; Jн – ток в нагрузке; Ф – магнитный поток; W – число витков катушки

При этом изменяется сопротивление магнитному потоку, изменяется индуктивность катушки и комплексное сопротивление катушки:

На рисунке 4.2 представлен cоленоидальный преобразователь.

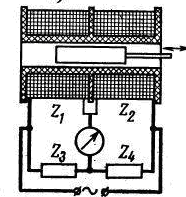
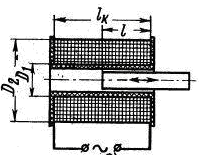
а) б)

Рисунок 4.2. Индуктивные сонолеидальные преобразователи: а – дифференциальный преобразователь; б – соленоидальный преобразователь; Z₁ – Z₄ – плечи моста; Д₁, Д₂ – габаритные размеры преобразователя

Линейные перемещения от l до 2000 мм. Индуктивность катушки L равна

,

где μ_ж – магнитная проницаемость сердечника.

На рисунке 4.3 представлен трансформаторный преобразователь с изменением зазора

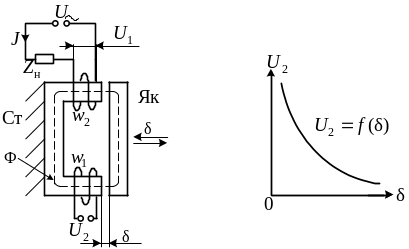
Рисунок 4.3. Трансформаторный преобразователь перемещения

При изменении воздушного зазора изменяется сопротивление магнитному потоку, при этом изменяется комплексное сопротивление катушки w₁, следовательно изменяется и падение напряжения на этой обмотке, U_1, вместе с Z_н они образуют делитель напряжения, следовательно, будет изменяться выходное напряжение

.

На рисунке 4.4 изображены разновидности конструкций и схем трансформаторных индуктивных преобразователей.

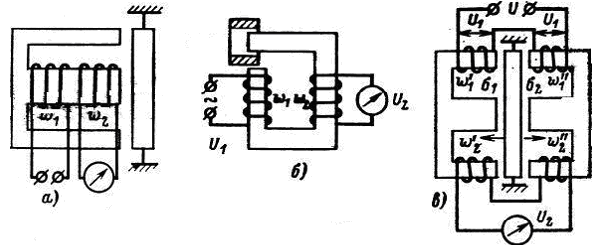
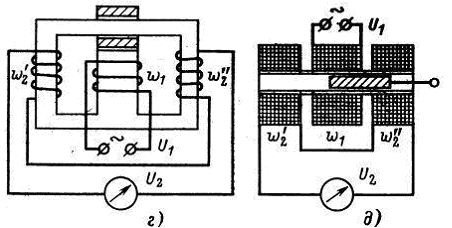
Рисунок 4.4. Конструкции и схемы трансформаторных индуктивных преобразователей

На рисунке 4.5 представлены конструкции и схемы включения дифференциальных индуктивных преобразователей

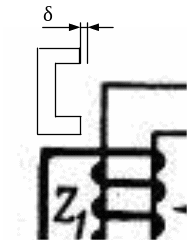
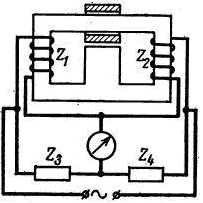
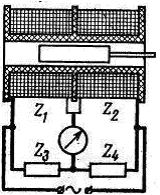
а) б) в)

Рисунок 4.5. Конструкции и схемы включения дифференциальных индуктивных преобразователей: а – с переменным зазором; б – с переменной площадью экрана ; в – соленоидного типа

Дифференциальной называется схема потому, что при уменьшении δ₁ будет увеличиваться зазор δ₂, т.е изменяться с разными знаками. При изменении зазоров δ изменяется комплексные сопротивления Z₁ и Z ₂ . При этом увеличивается в два раза чувствительность, уменьшается подавляющее большинство погрешностей, внешние влияния с одинаковым знаком компенсируются, расширяется линейный участок характеристики (до 30 %). Такая схема обнаруживает направление изменения δ и используется в фазочувствительных схемах.

5. МАГНИТОУПРУГИЕ ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ

Принцип работы заключается в следующем: если подвергнуть механическим деформациям ферромагнитный сердечник, то можно наблюдать изменение его магнитной проницаемости (рисунок 5.1.):

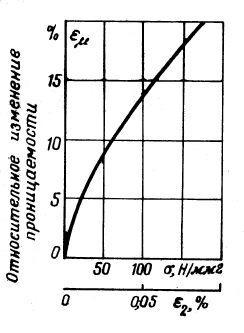
Рисунок 5.1. – график изменения относительной магнитной проницаемости железа армко от механического напряжения

При изменении магнитной проницаемости под воздействием давления изменяется индуктивность преобразователя и, следовательно, полное сопротивление катушки и тока, протекающего через катушку: р-σ-μ-L-Z-I:

где S_ж – сечение железа, l – длина магнита, – сопротивление потерь в стали, ω – круговая частота, Ф – эффективное значение магнитного потока в сердечнике, – сопротивление потерь в стали. Полное сопротивление катушки:

,

– активное сопротивление магнитопровода ;

– реактивная составляющая сопротивления (вихревые токи, потери на гистерезис); – мощность потерь в стали ; - круговая частота источника питания; Ф – эффективное значение магнитной индукции.

Рисунок 5.2. Конструкции и схемы магнитоупругих преобразователей: а, б – дроссельные; в – трансформаторные; д – преобразователь со скрещёнными обмотками

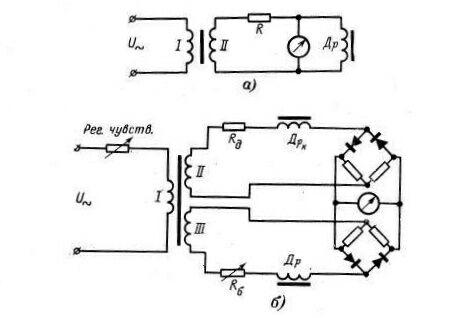
Рисунок 5.3. схемы включения магнитоупругих преобразователей: а – последовательная; б – компенсационная; Др – магнитоупругие преобразователи; Др_к – компенсационный преобразователь

Основными источниками погрешности являются: температурная погрешность (μ=f(t⁰)) и погрешность от гистерезиса. Для уменьшения этих погрешностей используется дифференциальная измерительная схема. Схемы включения магнитоупругих преобразователей приведены на рисунке 5.3.