3.2. Визначаємо коефіцієнт теплопередачі у зонах з суцільною теплоізоляцією і підкріплюючими елементами.

Схема теплоізоляційної конструкції бокової стіни вагона

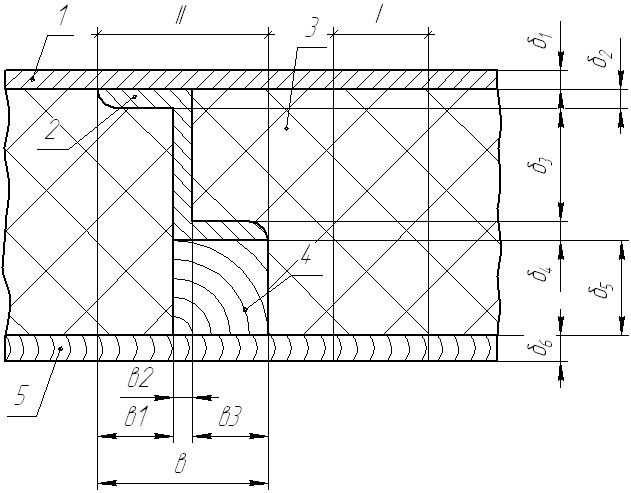
ІІ – зона з підкріплюючим елементом;

І – зона з неперервним теплоізоляційним шаром.

1 – зовнішня металева оболонка; 2 – стальний підкріплюючий елемент; 3 – теплова ізоляція; 4 – дерев’яний брусок; 5 – внутрішня оболонка столярної плити.

Для розрахунку коефіцієнтів теплопередачі у зонах з суцільною теплоізоляцією і підкріплюючим елементом використовують такі методи:

• метод теплових балансів;

• метод кругових теплових потоків;

• метод елементарних перерізів.

Метод елементарних перерізів передбачає два способи розрахунку коефіцієнта теплопередачі в зонах з підкріплюючим елементом.

Перший спосіб полягає в тому, що теплоізоляційна конструкція умовно розділяється, в напрямку теплового потоку, нескінченно тонкими, абсолютно нетеплопровідними мембранами.

Другий спосіб полягає втому, що зона з підкріплюючим елементом розподіляється нескінченно тонкими, але теплопровідними перпендикулярними до напрямку теплового потоку, мембранами.

Визначаємо коефіцієнт теплопередачі в зоні з неперервним шаром ізоляції за формулою:

(3.3)

(3.4)

Коефіцієнт теплопередачі в зоні з неперервним шаром ізоляції

Метод елементарних перерізів (спосіб 1)

Щоб порахувати коефіцієнт теплопередачі, задачу приводять до розрахунку теплопередачі в багатошаровій стінці (тобто, кожну ділянку шириною b₁, b₂, b₃ розглядають як багатошарову стінку).

Коефіцієнт теплопередачі шукаємо за формулою:

(3.5)

Значення коефіцієнта теплопередачі К для першої ділянки визначаємо за формулою:

(3.6)

де, α_з – коефіцієнт тепловіддачі на зовнішній поверхні кузова;

α_в - коефіцієнт тепловіддачі на внутрішній поверхні кузова.

Коефіцієнт теплопередачі для другої ділянки визначаємо за формулою:

(3.7)

Коефіцієнт теплопередачі для третьої ділянки визначаємо за формулою:

(3.8)

Значення коефіцієнта теплопередачі в цьому способі має занижену величину, тому що обмежена можливість переходу теплового потоку в зони з більшою теплопровідністю.

Метод елементарних перерізів (спосіб 2)

Зводимо цей спосіб до моделі багатошарової стінки. При цьому, розглядаємо кожні, перпендикулярні напрямку теплового потоку, ділянки як теплові опори, які з’єднані послідовно.

Коефіцієнт теплопровідності для першої ділянки рівний:

Коефіцієнт теплопровідності для другої ділянки рівний:

(3.9)

Коефіцієнт теплопровідності для третьої ділянки рівний:

(3.10)

Коефіцієнт теплопровідності для четвертої ділянки рівний:

(3.11)

Коефіцієнт теплопровідності для п’ятої ділянки рівний:

(3.12)

Коефіцієнт теплопровідності для шостої ділянки рівний:

Коефіцієнт теплопередачі рівний:

(3.13)

Цей спосіб дає завищене значення коефіцієнта теплопередачі, тому що він передбачає можливість переходу теплового потоку в зону з меншим термічним опором.

Визначивши значення коефіцієнта теплопередачі за двома способами, визначаємо середнє за формулою:

(3.14)