§ 4.4. Расчет червячных передач

Червячные передачи, так же как и зубчатые, рассчитывают по контактным напряжениям и напряжениям изгиба. В отличие от зубчатых передач, где основным видом повреждения является усталостное выкрашивание рабочих поверхностей зубьев, в червячных передачах чаще наблюдается заедание и износ. Для предупреждения заедания ограничивают значения контактных напряжений и применяют антифрикционные материалы. Червяк изготавливают из стали с термообработкой до твердости HRC > 45 (закалка ТВЧ, цементация), колесо из бронзы или чугуна.

В стандартных червячных редукторах типа Ч применяется червячная передача с цилиндрическим червяком. Витки червяка закалены до 50...55 HRC, венцы червячных колес изготовлены из оловянно-фосфористой бронзы. Последовательность расчета червячных передач стандартных редукторов, аналогична расчету зубчатых передач. Основные геометрические параметры червячных передач регламентированы ГОСТ 2144-76.

1. Определяют основные геометрические параметры передачи.

При заданном межосевом расстоянии а_w и передаточном числе U_ред по ГОСТ 2144-76 (табл. 4.5) уточняют соотношение z₂ : z₁, выбирают модуль зацепления m, коэффициент диаметра червяка q, коэффициент смещения X. При выборе соотношения z₂ : z₁ учитывают следующие рекомендации: принимают число заходов червяка z₁ = 4 при U = 8...15, z₁ = 2 при U = 15...30, z₁ = 1 при U > 30.

Для увеличения жесткости червяка значение коэффициента q принимают не менее 0,25Z₂.

Определяют угол подъема винтовой линии червяка  (рис. 4.3):

(4.22)

Таблица 4.5. Основные параметры цилиндрических червячных передач

(по ГОСТ 2144–76. С сокращениями)

U	8; 16; 31,5	10; 20; 40	12,5; 25; 50	63	80
z2: z1	32:4; 32:2; 32:1	40:4; 40:2; 40:1	50:4; 50:2; 50:1	63:1	80:1
aw	m; q; x
40	2; 8; 0	1,6; 10; 0	1,25; 12,5; +0,75	1,0; 16; +0,5	–
63	3,15; 8; 0	2,5; 10; +0,2	2; 12,5; +0,25	1,6; 16; +0,125	–
80	4; 8; 0	3,15; 10; +0,4	2,5; 12,5; +0,75	2; 16; +0,5	1,6; 20; 0
100	5;8;0	4; 10; 0	3,15; 12,5; +0,496	2,5; 16; +0,5	2;20;0
125	6,3; 8; -0,16	5; 10; 0	4; 12,5; 0	3,15; 16; +0,18	2,5; 20; 0
160	8;8;0	6,3; 10; +0,397	5; 25,5; +0,75	4; 16; +0,5	3,15; 20; +0,794

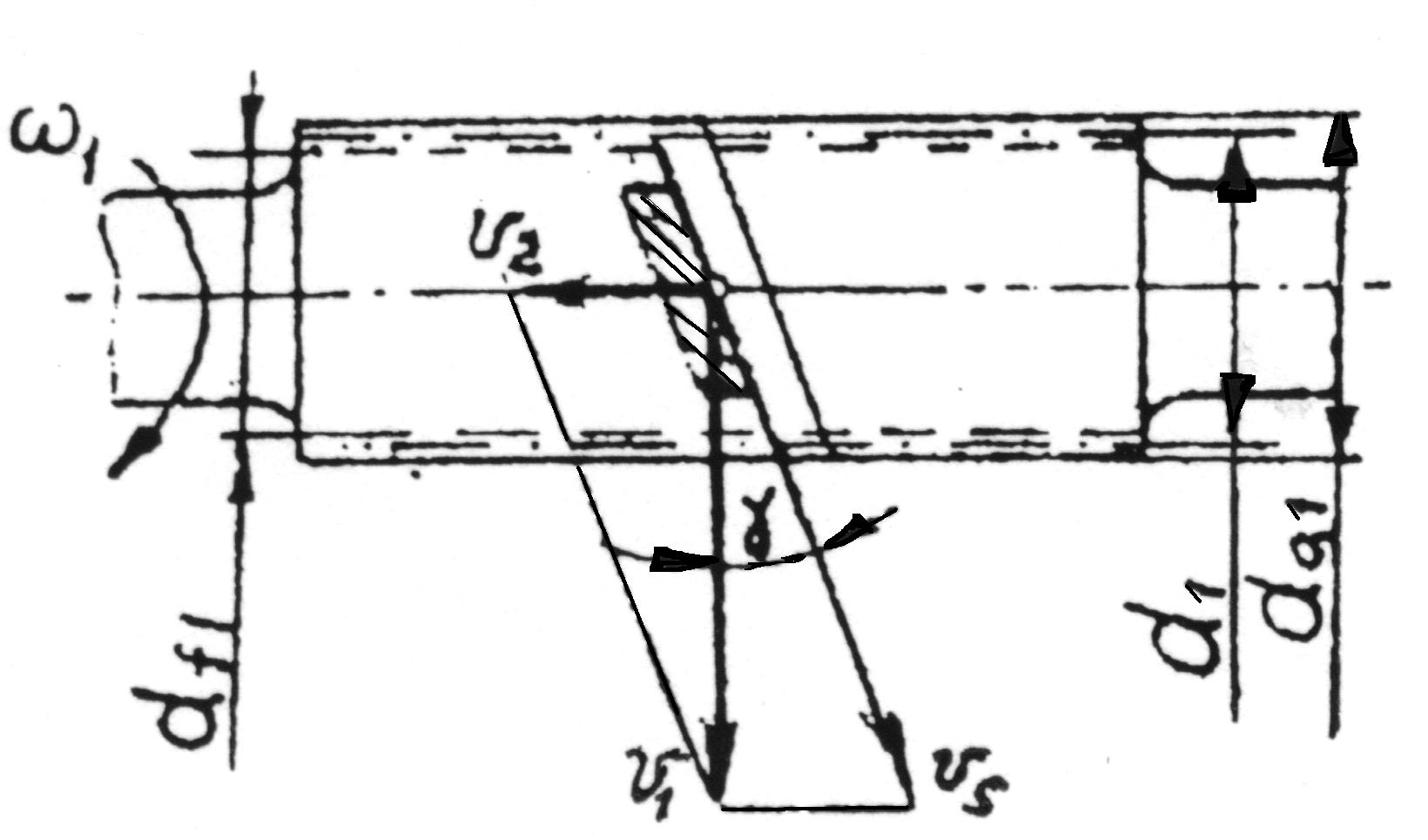
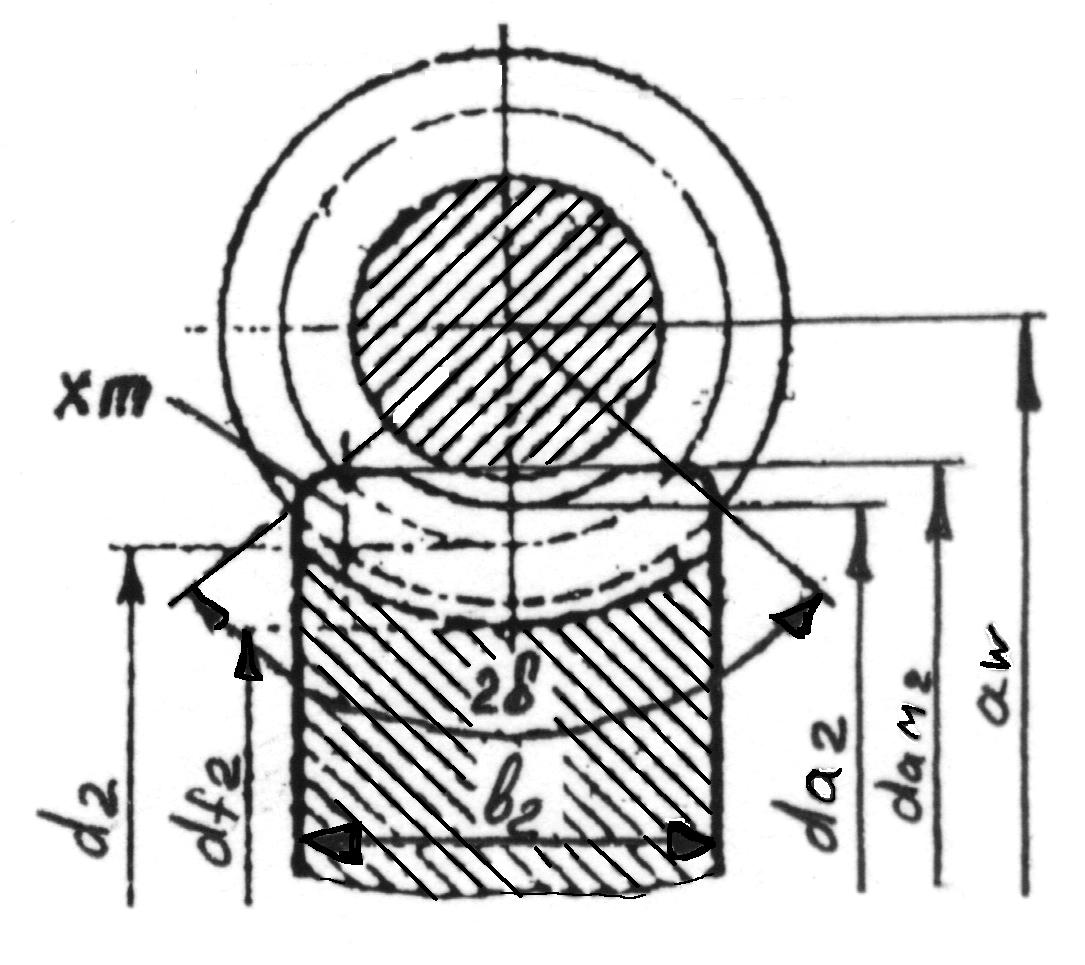
Рис. 4.3 Рис. 4.4

Диаметры червяка (рис. 4.3):

Диаметры червячного колеса (рис. 4.4):

Ширина зубчатого венца червячного колеса b₂  0,75d_a1 при z₁ = 1 или 2;

b₂  0,67d_a1 при z₁ = 4;

полученные значения у

точняют по ГОСТ 6636-69 (табл. П.5.1, прил. 5).

2. Определяют величину контактных напряжений _Н:

(4.23)

где Т₂ – крутящий момент на колесе, Н·м;

К_н – коэффициент нагрузки, приближенно можно принять К_Н = 1,2;

[_н] – допускаемые контактные напряжения;

для безоловянных бронз [_н] = 300 – 25V_s, (4.24)

где V_s – скорость скольжения, V_s = V₁ / cos, (4.25)

V₁ – окружная скорость червяка, (4.26)

Для оловянных бронз [_н] = 0,9_B (4.27)

Механические характеристики марок бронз, используемых для изготовления - венцов червячных колес, представлены в табл. 4.6.

Полученные значения _H сравнивают с допускаемыми [_н] и по табл. 4.6 уточняют марку бронзы.

Таблица 4.6. Механические характеристики бронз

Материал колеса	Способ отливки	Механические характеристики, МПа
		т	в
Бр ОФ 10-1	В песок	120	200
Бр ОФ 10 -1	В кокиль	150	260
Бр ОНФ	Центробежн.	170	290
Бр А9ЖЗЛ	В песок	200	400

3. Проводят проверочный расчет по напряжениям изгиба:

(4.28)

где Y_F – коэффициент формы зуба червячного колеса, определяется по числу зубьев эквивалентного колеса z_V (табл. 4.7);

(4.29)

m_n – модуль в нормальном зацеплении, m_n = mcos; (4.30)

Таблица 4.7. Значения коэффициента Y_Е

zv	20	24	26	28	30	32	35	37	40	45	50	60	80
Yр	1,98	1,88	1,85	1,80	1,76	1,71	1,64	1,61	1,55	1,48	1,45	1,40	1,40

F_t – окружная сила в зацеплении,

(4.31)

K_F – коэффициент нагрузки, приближенно К_F = 1,2...1,3;

[_F] – допускаемое напряжение изгиба, для всех марок бронз можно принять

[_F] = 0,25_T + 0,08_B (4.32)

4. Определяют силы в зацеплении (Рис. 4.5):

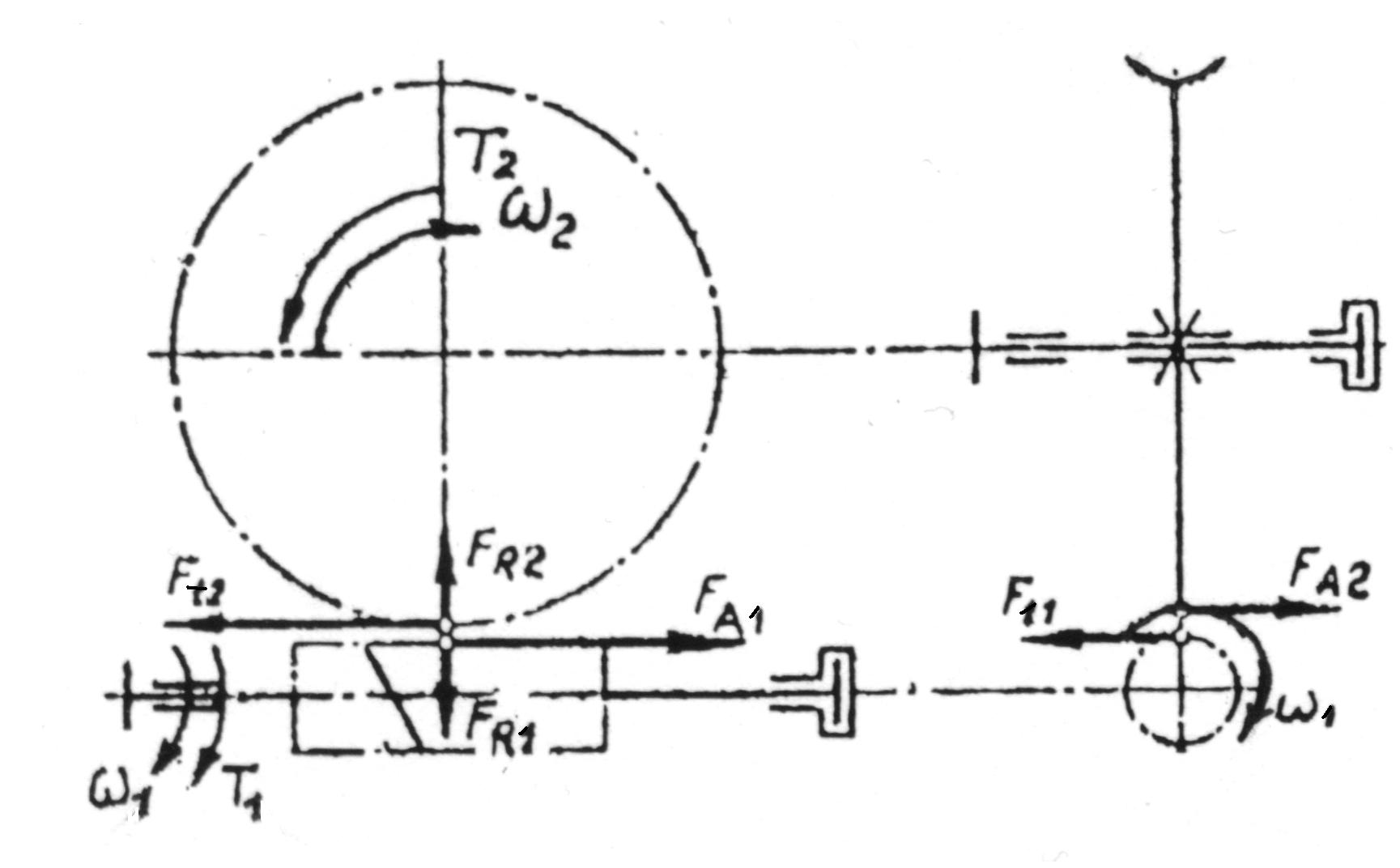
Рис. 4.5

Пример расчета. Выполнить расчет передачи червячного редуктора типа Ч.

Исходные данные: крутящий момент на тихоходном валу редуктора Т_тих = 480Н·м,

передаточное число редуктора U_ред = 25, частота вращения вала червяка n₁ = 960 мин^–1.

1. Типоразмер редуктора по каталогу выбираем по условию(§ 4.1)

(1,4…1,5)T_тих = 1,4·480 = 672 Н·м  T_{н тих}

По табл. П.2.9 прил. 2 выбираем редуктор Ч-125 (при выборе учитывается значение передаточного числа редуктора и частоты вращения червяка n₁). Уточняем его основные параметры: момент на тихоходном валу T_{н тих} = 700 Н·м, межосевое расстояние передачи

а_w = 125 мм, вариант сборки – 51 (рис. П.2.9), вариант расположения – 1, концы быстроходного и тихоходного валов – цилиндрические (Ц), КПД редуктора  = 0,84. Обозначение редуктора: Ч-125-25-51-1Ц-УЗ.

2. Определяем основные геометрические параметры передачи. По ГОСТ 2144-76

(табл. 4.5) при а_W = 125 мм, U_ред = 25 принимаем: z₂ : z₁ = 50 : 2; модуль m = 4мм;

коэффициент диаметра червяка q = 12,5; коэффициент смещения x = 0.

Определяем угол подъема винтовой линии червяка по ф–ле (4.22):

Диаметры червяка:

Диаметры червячного колеса (при х = 0):

Ширина зубчатого венца червячного колеса (п. 1)

по ГОСТ 6636–69 (табл. П.5.1)

принимаем b₂ = 42 мм.

3. Определяем величину контактных напряжений по ф–ле (4.23):

Коэффициент нагрузки (п. 2) принимаем К_h = 1,2.

Определяем скорость скольжения по ф–ле(4.25):

Окружная скорость червяка по ф–ле (4.26):

Возможно использование безоловянистых бронз. Допускаемые напряжения для безоловянистых бронз по ф–ле (4.24):

, что недопустимо. Для оловянистых бронз по ф–ле (4.27): .

Наибольший предел прочности _в имеет бронза марки Бр ОНФ, _В = 290 МПа, предел текучести _т = 170 МПа (табл. 4.6);

, условие расчета выполняется.

4. Выполняем проверочный расчет передачи по напряжениям изгиба. По ф–ле (4.28)

.

Коэффициент формы зуба Y_F определяем по табл. 4.7.

Число зубьев эквивалентного колеса по ф–ле (4.29)

Окружная сила по ф–ле (4.31)

Коэффициeнт нагрузки (п. 3) K_F = l,25. Модуль в нормальном сечении по ф–ле (4.30)

Допускаемые напряжения изгиба по ф–ле (4.32)

Напряжения изгиба

Условие прочности выполняется.

5. Определяем силы в зацеплении: