Величина ε0 определяется потребностями геологической службы, например, нужным сечением δ прогнозной структурной карты.

Постановку указанных задач удобно продемонстрировать на конкретном примере. Пусть геологическим заданием предусмотрено изучение строения кровли кристаллического фундамента в рамках некоторого планшета (рис.3.5). В результате должна быть получена соответствующая структурная карта с сечением изогипс Δ=250 м.

Для решения этой задачи была проведена гравиметрическая и магнитная съемка в масштабе, обеспечившим построение кондиционных карт аномалий Δg и ΔТ, а также выполнены опытные сейсмические исследования КМПВ по трем профилям, расположенным так, как показано на рис.3.5 .

Подобная ситуация характерна при региональных геофизических исследованиях на первой стадии геолого-поисковых работ, направленных на изучение геологического строения крупного региона и поиски месторождений полезных ископаемых, в частности, нефти и газа в осадочной толще.

Наблюдения КМПВ, проведенные по системе, ориентированной на регистрацию волн от поверхности кристаллического фундамента в первых вступлениях, дают значения глубин Н_φ вдоль профилей I,II,III. Однако, этих сведений безусловно недостаточно для построения кондиционной структурной карты. Вместе с тем иметь такую структурную основу при проектировании следующей – поисковой стадии исследований чрезвычайно важно, так как в силу унаследованности геологического развития, закономерности формирования структур осадочного чехла во многом предопределены строением фундамента.

Конечно, выбор оптимальных направлений для поисков облегчается качественным анализом данных гравиразведки и магниторазведки, районированием территории по особенностям этих полей, предположениями о геологической природе выявленных в процессе районирования аномалий Δg и ΔТ и т.п. Тем не менее ни эти, ни какие-либо другие геолого-геофизические материала не могут вполне заменить собой структурную основу.

Получить ее с использованием указанных выше исходных данных позволяют корреляционные методы интерпретации. Для этого нужно вначале изучить характер связи между Н_φ ,Δg и ΔТ, пользуясь формальной постановкой задачи (I) и точками профилей I,II и III как эталонным пространством φ. Затем с учетом этих связей и на основе соотношения (2) осуществляется прогноз глубин Н_φ во всех остальных точках планшета, которые следует в целом рассматривать как прогнозное пространство ψ.

Важнейшими моментами процедуры прогнозирования в рамках корреляционных методов является обоснование правомерности применения принципа аналогий и независимый контроль качества прогнозного оператора связи.

Утверждение о справедливости принципа аналогий всегда носит качественный характер и должно рассматриваться как рабочая гипотеза, поскольку строгое его обоснование возможно только при исчерпывающих сведениях о геологическом строении исследуемой территории.

Рис. 3.5. Схема расположения эталонных и контрольных данных.

Условные обозначения:

1- изоаномалы поля силы тяжести в редукции Буге (мГл);

2- изодинамы полного вектора напряженности магнитного поля;

3 – профили КМПВ с номерами эталонных точек;

4 –профили КМПВ с номерами контрольных точек.

Тем не менее, есть положения в существенной мере контролирующие соблюдение указанного принципа:

1. Принадлежность эталонной и прогнозной территории к единой геоструктуре.

2. Идентичность статистических свойств геофизических полей эталонной и прогнозной областей.

Если первое положение, гарантирующее генетическое единство связи многих физических и геологических характеристик разреза, далеко не всегда очевидно, то второе, обосновывающее правомерность использования статистической процедуры прогноза, вполне может быть проверено на уровне статистических гипотез [18]. На практике, однако, часто ограничиваются простым сопоставлением поведения полей на эталонном и прогнозном пространстве.

Независимый контроль качества корреляционной процедуры, как правило, осуществляется в точках эталонного пространства, которые не использовались в формировании прогнозного оператора. При этом за ошибку прогноза ε_n принимается величина

ε_n = max(ε_φ, ε_k)

где ε_φ и ε_k – ошибки прогнозного оператора, соответственно, на эталонной и контрольной выборках.

Результаты такого контроля, конечно, зависят от представительности используемых выборок. Поэтому большие величины ε_k должны настраивать интерпретатора не на категорический отказ от использования корреляционной процедуры, а на углубленный анализ исходных данных, свойств и качества эталонного пространства.

Парные корреляционные связи.

Методы прогноза, основанные на связи двух параметров – геологического (Н) и какого-либо геофизического (например Δg) – наиболее просты, однако, во многих случаях точность такого прогноза оказывается низкой (ошибка приближения ε – велика), поскольку из-за суммарного характера наблюденных геофизических полей не всегда удается подобрать геофизический параметр тесно корреляционно связанный с изучаемой геологической границей.

Наглядное представление о парной взаимосвязи анализируемых величин дают корреляционные графики (поля корреляции). На рис 3.6 приведен график корреляции глубин залегания кристаллического фундамента Н_ф и аномалий поля Δg, построенный по точкам эталонного пространства. Исходные профильные кривые Н_ф и Δg показаны на рис 3.7. Значения Н_ф и Δg в отсчетных точках профилей являются ординатами и абсциссами соответствующих точек на корреляционном графике. Вытянутость всего “облака” точек вдоль некоторой прямой характеризует тесноту линейной парной корреляционной связи Н_ф и Δg.Если поверхность Н_ф является достаточно сильной гравиактивной границей (скачок средневзвешенного значения плотности порядка 0.2г/см³ и более) и в толще осадочного чехла нет столь же резких перепадов плотности, экранирующих гравитационное влияние фундамента, то вязь Н_ф с Δg может быть действительно близка к линейной.

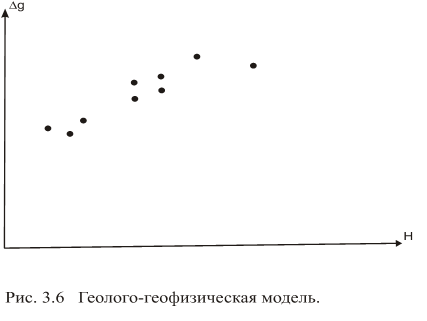
Тогда целесообразность ее аппроксимации прямой вида Н_ф=А₀+А₁Δg, называемой прямой парной регрессии, становится очевидной. Коэффициенты А₀ и А₁ в данном случае конкретизируют вид прогнозного оператора А_φ из уравнения (1).

Оптимальная аппроксимация, дающая наиболее вероятное положение линии регрессии на плоскости (Н_ф , Δg)_φ, выполняется методом наименьших квадратов [10]. При этом минимизируется сумма квадратов отклонений ΔН исходных значений Н_i от отсчетов, полученных по регрессионной прямой

(3.3)

Здесь N – объем выборки точек эталонного пространства φ. Дифференцируя (3) по неизвестным коэффициентам А₀ и А₁ с учетом линейности оператора суммирования , получим систему уравнений, которые принято называть нормальными [18]:

(3.4)

Решить систему (4) относительно А₀ и А₁ и таким образом конкретизировать вид оператора А_φ несложно. Действительно, из первого уравнения системы имеем

(3.5)

где и - средние значения Н и Δg эталонной выборки.

Умножим теперь первое уравнение на , второе – на N и рассмотрим их разность.

Отсюда получим

(3.6)

Более удобный вид для коэффициента А₁ получается, если поделить числитель и знаменатель формулы (6) на N² :

(3.7)

Здесь - среднее значение произведения Н и Δg в пределах эталонной выборки;

- средний квадрат наблюденного поля Δg в пределах эталонной выборки.

В таком виде числитель и знаменатель в формуле (7) имеют смысл известных выборочных статистических оценок – ковариаций [18].

(3.8)

и дисперсии

(3.9)

Убедиться в этом можно просто раскрыв скобки в формулах (8) и (9) с учетом того, что и в рамках используемой эталонной выборки – величины постоянные. Тогда коэффициент А₁ запишется в компактном виде

(3.10)

Ковариация, как известно, является показателем тесноты взаимосвязи Δg и Н, однако, чтобы не учитывать размерности и размаха величин Δg и Н, удобнее пользоваться нормированной оценкой, называемой коэффициентом корреляции [18]:

(3.11)

где D(Н) – оценка дисперсии глубин Н на используемой эталонной выборке.

Пределы изменения этой величины определяются соотношением

-1≤r(Δg,Н)≤1 (3.12)

Равенство r=нулю означает полное отсутствие линейной связи между величинами Δg и Н (при этом другой, нелинейный, тип связи отнюдь не исключен). По мере приближения r к ±1 статистическая (корреляционная) связь параметров стремится к линейной функциональной зависимости.

Теперь с учетом (5) и (7) уравнение линейной регрессии Н=А₀+А₁∆g можно представить в следующем виде

(3.13)

Отсюда (3.14)

Используя статистические оценки (8) и (9), получим

(3.15)

или, имея в виду формулу (11):

(3.16)

Здесь , - оценки среднеквадратических отклонений (стандарты) величин ∆g и Н в пределах эталонной выборки [18].

Таким образом, из формулы (16) хорошо видно, что коэффициенты оператора связи Aφ в данном случае определяются теснотой корреляции геолого-геофизических параметров и величинами их стандартов.

Погрешность вычисления коэффициентов характеризуется среднеквадратической ошибкой подсчета корреляции :

(3.17)

Следовательно, увеличением мощности эталонной выборки достигается более точная аппроксимация зависимости Н от ∆g.

Однако, получив близкую к единице величину r( ∆g,H) и малую ошибку δ(r) , еще нельзя утверждать, что значения Н определяются найденным регрессионным оператором в точках эталонного пространства с требуемой для прогнозирования точностью.

Наилучшим показателем в этом смысле является вычисляемая в прогнозной постановке задачи (2) среднеквадратическая ошибка прогноза (приближения) Н по ∆g:

(3.18)

где - значения Н из уравнений (13) - (16) .

Если в формулу (18) подставить Н из уравнения (16) и провести соответствующие преобразования, нетрудно получить выражение для в несколько ином виде:

(3.19)

Здесь хорошо видно, что ошибка приближения тем больше, чем больше природная дисперсия Н и уменьшается с возрастанием тесноты корреляционной взаимосвязи Н и ∆g.

Положим, например, стандартное отклонение Н_ф равным 500м (такое значение S(Н) характерно для ряда площадей бортовой зоны Прикаспийской впадины), тогда при r( ∆g,H)=0,9 ошибка приближения по формуле (19) составит 218м. Таким образом, высокое само по себе значение коэффициента корреляции в конкретных геолого-геофизических условиях оказалось недостаточным для прогноза с малой ошибкой.

Как уже говорилось, во многих случаях парная корреляционная взаимосвязь геолого-геофизических параметров оказывается довольно слабой. Это чаще всего объясняется суммарным характером большинства геофизических полей. Аномалии ∆g, например, обусловлены помимо одной-двух резких гравиактивных поверхностей, целым рядом слабых плотностных границ геологического разреза, конфигурация которых может существенно отличаться от формы поверхности сильных границ. Указанное обстоятельство ослабляет корреляцию ∆g с Н и, следовательно, способствует увеличению ε_n.

Многомерные корреляционные связи.

В условиях сильной “ засоренности” геофизического поля мешающими факторами можно уменьшить величину среднеквадратической погрешности ε_n, переходя от парной линейной корреляционной взаимосвязи параметров к множественной.

Весьма характерная ситуация, иллюстрирующая целесообразность такого перехода при картировании кровли кристаллического фундамента, приведена в [9]. На рис.3.8. Хорошо видно, что парная корреляция гипсометрии поверхности кристаллического фундамента, как с гравитационным Δg, так и с магнитными ΔТ полями, слабая. Форма аномальной кривой Δg обусловлена на такой модели двумя факторами: моноклинальным погружением кристаллического фундамента, сложенного гранито-метаморфическими породами и гравитационным влиянием базальтовых интрузий, пронизывающих его толщу. Поле ΔТ сформировано в основном магнитоактивными базальтами, в то время как вмещающие их метаморфические породы фундамента слабо намагничены и в нем не отражаются. Если теперь составить регрессионное уравнение вида

Н_ф=А₀+А₁Δg+А₂ΔТ, (3.20)

то есть включить в оператор А_φ разные парные корреляционные связи – сделать его многомерным, - прогноз Н_ф будет более эффективным. Иными словами, многомерная связь должна быть теснее, чем парная, а ошибка приближения ε_п(Н/Δg, ΔТ) – меньше, чем ε_п(Н/Δg) или ε_п(Н/ΔТ).

В приведенном примере составление и использование многомерного оператора равносильно исключению влияния базальтовых тел, зафиксированного в рельефе кривой ΔТ, из поля Δg. В результате кривая Δg как бы исправится, то есть ее связь с гипсометрией фундамента станет более тесной.

Приемы вычисления коэффициентов многомерной регрессии ничем не отличаются от парного случая.

Образовав в точках эталонного пространства (Н,Δg,ΔТ)_φ разности

А₀+А₁Δg_i+А₂ΔТ_i - Н_i = ΔН_i ,

минимизируют сумму их квадратов:

(3.21)

Дифференцируя формулу (21) по А₀,А₁ и А₂ с учетом линейности оператора суммирования, переходят к системе нормальных уравнений:

(3.22)

Решая ее относительно коэффициентов регрессионного оператора А₀,А₁ и А₂ получают

(3.23)

(3.25)

(3.24)

Оценкой тесноты многомерной корреляционной связи служит множественный (сводный) коэффициент корреляции [10]:

(3.26)

Он обладает теми же свойствами, что и r в случае парной регрессии. Множественный коэффициент R равен нулю, когда линейная статистическая взаимосвязь между параметрами Н,Δg и ΔТ полностью отсутствует (отметим еще раз, что это отнюдь не исключает наличия между ними какого-либо иного типа связи). Стремление R к единице соответствует переходу статистической линейной зависимости в функциональную.

Если поля Δg и ΔТ информативны в отношении Н, величина R превосходит значения коэффициентов парной корреляции. Тогда и ошибка приближения, равная для многомерного случая

(3.27)

уменьшится в сравнении с парным, а точность прогнозирования соответственно увеличится

Силу “влияния” каждого из прогнозирующих параметров на Н в многомерной связи уже нельзя измерить по величине парных коэффициентов r(Δg,H) и r(ΔT,H) – они дают лишь приближенную оценку корреляции. Более объективно охарактеризовать это “влияние”, то есть по сути дела сопоставить “информативность” прогнозирующих параметров, позволяют так называемые частные коэффициенты корреляции:

, (3.28)

(3.29)

В этих выражениях влияние третьего параметра, вынесенного за скобки в левых частях равенств, исключается и, таким образом, связь Δg или ΔТ с Н измеряется в относительно чистом виде.

Хотя за счет увеличения числа членов регрессионного уравнения ошибка приближения ε_п, посчитанная в эталонных точках, уменьшается, описать зависимость между Н и геофизическими данными с необходимой для решения прогнозной задачи точностью удается не всегда. Действительно, большое число прогнозирующих параметров приводит к излишней “индивидуализации” оператора связи А_φ, и он не выдерживает процедуры независимого контроля, то есть ошибка на контрольной выборке ε_к, вычисляемая по формуле (18), оказывается недопустимо большой. Происходит это потому, что параметр, информативный на эталоне, в прогнозной области может вести себя незакономерно, а его включение в оператор связи снижает достоверность последующего прогнозирования. Кроме того, далеко не всегда использование множественной регрессии позволяет скорректировать суммарный характер геофизических полей.