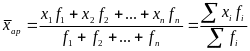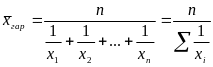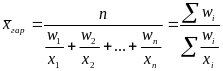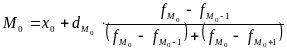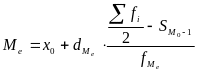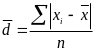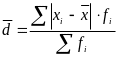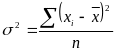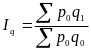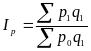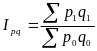- •Методические указания по дисциплине статистика
- •Паспорт программы учебной дисциплины «статистика»
- •1.1. Область применения программы
- •1.2. Место учебной дисциплины в структуре основной профессиональной образовательной программы:
- •1.3. Цели и задачи учебной дисциплины – требования к результатам освоения учебной дисциплины:
- •1.4. Количество часов на освоение программы учебной дисциплины:
- •3. Условия раелизации учебной дисциплины
- •3.1 Требования к минимальному материально-техническому обеспечению
- •3.2 Информационное обеспечение обучения
- •4. Контроль и оценка результатов освоения учебной дисциплины
- •Методические рекомендации для выполнения контрольной работы
- •Домашняя контрольная работа
- •Критерии оценки самостоятельной работы студентов
Методические рекомендации для выполнения контрольной работы
Приступая к изучению предмета необходимо ознакомиться с содержанием программы и составить план занятий, т. е. разделить материал на последовательно изучаемые темы. После этого в каждой теме следует выделить основные вопросы, чтобы затем, в процессе изучения материала, найти на них ответы.
Одним из важнейших средств активизации самостоятельной творческой деятельности студентов является умение решать задачи. Для этого необходимо внимательно изучить условие задачи, проанализировать содержание, выяснить закономерности и правила, лежащие в основе её решения.
Конечно, общих рецептов для решения разнообразных задач не существует, однако рекомендуем придерживаться следующих советов:
Внимательно изучите цель, поставленную в задаче; выясните, какие теоретические положения связаны с данной задачей в целом или с некоторыми её элементами.
Не следует приступать к решению задачи, не обдумав её условия и не найдя плана решения.
Попробуйте расчленить данную задачу на серию вспомогательных, последовательное решение которых может составить решение исходной задачи.
Найдя план решения, выполните его, убедитесь в необходимости и правильности каждого шага, произведите проверку решения.
Если решить задачу не удаётся, отыщите в учебной литературе уже решённую задачу, похожую на данную, изучите внимательно это решение и постарайтесь извлечь из него пользу для решения данной задачи.
Необходимо приучить себя к постоянному самоконтролю в процессе своей работы. При решении задачи следует приучиться проверять каждый свой шаг, оценивать его разумность, рациональность, необходимость и полезность.
При этом могут использоваться различные приемы самоконтроля: проверка результатов решения задачи, проверка по аналогичному заданию, оценка соответствия результата здравому смыслу.
Решив задачу, проанализируйте решение, отметьте, что нового при этом вы узнали и приобрели. Постарайтесь запомнить и усвоить те приёмы, которые вы использовали. Все это пригодится при решении других задач.
Домашняя контрольная работа по курсу «Статистика» включает в себя темы «Ряды распределения», «Средние показатели», «Показатели вариации», «Ряды динамики», «Экономические индексы», «Выборочное наблюдение».
При выполнении заданий контрольной работы надо обратить внимание на следующее:
«Построение ряд распределения» следует определить по имеющимся данным вид ряда распределения – дискретный или интервальный, в зависимости от чего выбрать соответствующий способ построения ряда, правильно определить группировочный признак, определить интервалы группировки, сформировать группы, подсчитать итоги по каждой группе и по совокупности в целом, оформить результат в табличном виде;
«Определение среднего значения признака, модального и медианного значения признака» следует определить вид данного ряда распределения, правильно выбрать способ нахождения среднего, модального и медианного значений ряда, провести все необходимые расчеты, сделать вывода по полученным данным;
Средняя арифметическая: |
|
простая |
взвешенная |
|
|
где
|
|
Средняя гармоническая: |
|
простая |
взвешенная |
|
|
где
-
индивидуальные значения варьирующего
признака (варианты или середины
интервалов); n
- число единиц совокупности;
|
|
Мода: |
|
|
|
где
х0
– нижняя граница модального интервала;
|
|
Медиана: |
|
|
|
где
х0
– нижняя граница медианного интервала;
|
|
«Проанализировать данное распределение с помощью показателей вариации» следует применять определение вариации и основных показателей вариации; уметь рассчитывать абсолютные показатели вариации: размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение; относительные показатели вариации: коэффициенты осцилляции, вариации;
Размах вариации: |
|
где
|
Среднее линейное отклонение: |
|
простая |
взвешенная |
|
|
где
-
индивидуальные значения варьирующего
признака (варианты или середины
интервалов);
|
|
Дисперсия: |
|
простая |
взвешенная |
|
|
где - индивидуальные значения варьирующего признака (варианты или середины интервалов); - среднее значение признака; n - число единиц совокупности; f1, f2, …, fn – веса (частоты) признака. |
|
Среднее квадратическое отклонение: |
|
|
|
где
|
|
Коэффициент вариации: |
|
|
|
где
|
|
Коэффициент осцилляции: |
|
|
|
где
|
|
«Анализ динамики изучаемого явления» следует применять определение динамического ряда и его видов; уметь рассчитывать основные показатели анализа динамики изучаемого явления: абсолютные приросты, темпы роста и темпы прироста рассчитанные базисным и цепным методами;
Абсолютные приросты: |
|
базисный метод расчета |
цепной метод расчета |
|
|
где уi , уi-1 – уровень ряда, у0 – базисный уровень ряда. |
|
Темпы роста: |
|
базисный метод расчета |
цепной метод расчета |
|
|
где уi , уi-1 – уровень ряда, у0 – базисный уровень ряда. |
|
Темпы прироста: |
|
базисный метод расчета |
цепной метод расчета |
|
|
где
|
|
«Изучение и анализ статистических данных на основе индексного метода» следует применять определение индекса и индексного метода; уметь правильно строить индивидуальные индексы; общие индексы в агрегатной форме; уметь анализировать данные на основе рассчитанных индексов;
Индивидуальные индексы: |
||
физического объема |
цен |
стоимости |
|
|
|
где
|
||
Общие индексы в агрегатной форме: |
||
физического объема |
цен |
стоимости |
|
|
|
где - количество продукции за отчетный (1) и базисный (0) период; - цена единицы товара (продукта) за отчетный (1) и базисный (0) период. |
||
«Выборочное исследование»
Выборочный метод - наиболее распространенный вид несплошного наблюдения, который состоит в частичном наблюдении единиц совокупности. Основной предпосылкой применения выборочного исследования является возможность судить о характеристиках генеральной (общей) совокупности по отобранной выборочной совокупности. При этом в основу отбора единиц для обследования положены принципы равных возможностей попадания в выборку каждой единицы генеральной совокупности.
Если при сплошном наблюдении непосредственно определяются характеристики совокупности, то при выборочном исследовании делаются только оценки параметров генеральной совокупности. Оценка – это приближенное значение искомой величины, полученное на основании результатов выборочного наблюдения, обеспечивающее возможность принятия обоснованных решений о неизвестных параметрах генеральной совокупности. Примером оценки генеральной средней является выборочная средняя, генеральной дисперсии - выборочная дисперсия.
Поскольку при оценке характеристик используется только выборочная совокупность, то разность между характеристиками выборки и генеральной совокупности составляет ошибку выборки. Она зависит от степени вариации изучаемого признака, численности выборки, методов отбора единиц в выборочную совокупность, принятого уровня достоверности результата исследования.
Используя выборочный метод, чаще всего оценивают два вида обобщающих показателей:
среднюю величину количественного признака
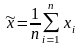 ,
где
,
где
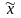 – среднее значение переменой в выборке
(выборочное среднее); n
– объем выборочной совокупности;
– среднее значение переменой в выборке
(выборочное среднее); n
– объем выборочной совокупности;долю (частость) альтернативного признака:
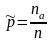 ,
где
,
где
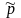 –
доля альтернативного признака в
выборочной совокупности;
–
доля альтернативного признака в
выборочной совокупности;
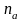 – число элементов совокупности,
индивидуальные значения которых
обладают свойством "а".
– число элементов совокупности,
индивидуальные значения которых
обладают свойством "а".
Возможные расхождения между характеристиками выборочной и генеральной совокупности измеряются средней ошибкой выборки, которая представляет собой среднее квадратичное отклонение возможных значений выборочных характеристик (оценок) от генеральных. Она определяется в зависимости от метода отбора.
При повторном отборе, когда каждая отобранная и обследованная единица возвращается в генеральную совокупность, где ей опять предоставляется равная возможность попасть в выборку, средняя ошибка выборки определяется следующим образом:
а)
для средней величины:
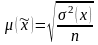 ,
где
,
где
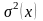 – дисперсия генеральной совокупности
(при проведении выборочных обследований
она, как правило, неизвестна, поэтому
на практике при расчете средней ошибки
выборки используется дисперсия
выборочной совокупности); n
- объем выборочной совокупности;
– дисперсия генеральной совокупности
(при проведении выборочных обследований
она, как правило, неизвестна, поэтому
на практике при расчете средней ошибки
выборки используется дисперсия
выборочной совокупности); n
- объем выборочной совокупности;
б)
для доли (частности):
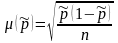 ,
где
,
где
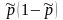 – дисперсия альтернативного признака.
– дисперсия альтернативного признака.
При бесповторном отборе, при котором повторное попадание в выборку одних и тех же единиц исключено, средняя ошибка выборки определяется следующим образом:
а)
для средней величины:
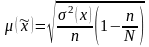 ,
где N
– объем генеральной совокупности;
,
где N
– объем генеральной совокупности;
б)
для доли (частности):
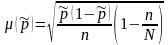 .
.
Если выборка достаточно велика (практически достаточно, чтобы ее объем составлял не мене 20 наблюдений), то считается, что ошибка распределена по нормальному закону. Но тогда, зная закон распределения ошибки, можно определить предельную ошибку выборки и тем самым оценить те границы интервала, за которые ошибка выйдет с заданной достаточно малой вероятностью (доверительной вероятностью). Такой интервал называется доверительный интервалом.
Теория
устанавливает соотношение между
предельной и средней ошибкой выборки,
гарантируемое с некоторой вероятностью:
 ,
где
,
где
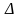 –
предельная ошибка выборки;
–
предельная ошибка выборки;
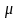 – средняя ошибка выборки; t
- коэффициент доверия.
– средняя ошибка выборки; t
- коэффициент доверия.
Коэффициент доверия определяется в зависимости от того, с какой доверительной вероятностью надо гарантировать результаты выборочного исследования, для определения t пользуются готовыми таблицами. Некоторые наиболее часто встречающиеся значения этого коэффициента приведены ниже:
Доверительная вероятность (Рдов) |
Коэффициент доверия (t) |
0,683 |
1 |
0,954 |
2 |
0,990 |
2,5 |
0,997 |
3 |
Таким образом, границы доверительного интервала могут быть представлены как:
а)
для средней величины:
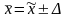 ,
то есть
,
то есть
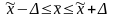 ;
;
б)
для доли (частности):
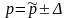 ,
то есть
,
то есть

Так как величина ошибки выборки зависит от численности выборочной совокупности n, при подготовке выборочного наблюдения возникает задача определения необходимой численности выборки – такой, которая обеспечит заданную точность результатов исследования.
При
повторном отборе необходимая численность
выборки определяется по формуле:
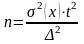 или
или
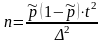 .
.
При
бесповторном отборе необходимая
численность выборки определяется по
формуле:
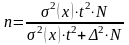 или
или
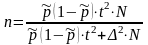 .
.