Приложение б

В настоящее время в условиях значительного роста объема перевозок грузов в городах для обеспечения более рационального использования подвижного состава и сокращения транспортных затрат большое значение имеет определение кратчайших расстояний между пунктами транспортной сети.

Транспортная сеть представляет собой систему дорог, которые пригодны по качеству дорожного покрытия, ширине проезжей части и открыты для движения подвижного состава.

Транспортная сеть состоит из отдельных элементов, которые являются вершинами и звеньями сети. Каждой вершине присваивается свой порядковый номер или другое условное обозначение.

Получим матрицу стоимости для нашего графа, элементами которой являются веса соответствующих дуг. Все элементы по диагонали матрицы приравнивняем к бесконечности

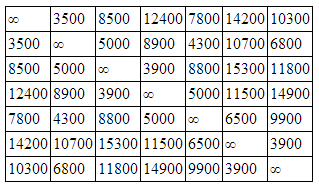
Найдем минимальные элементы в каждой строке и затем вычтем его из остальных элементов строки (минимальные элементы записаны напротив соответствующих строк). Получим матрицу представленную ниже.

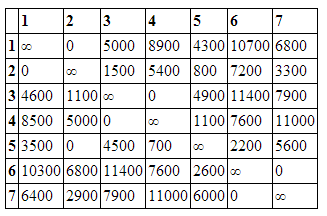
То же проделаем и со столбцами, не содержащими нуля. Получим матрицу, содержащую нули в каждой строке и каждом столбце.

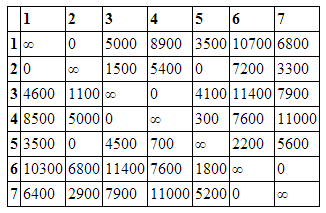
Для каждого нулевого элемента рассчитаем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Сij=0) и наименьшего элемента j столбца. Г_1,2=3500, Г_2,1=3500, Г_2,5=300, Г_3,4=1800, Г_4,3=1800, Г_5,2=700, Г_6,7=5100, Г_7,6=5100,  В результате сравнения мы получили 2 одинаковых максимальных Г=5100. Это означает что алгоритм разветвляется и мы должны рассмотреть все получившиеся варианты поочередно.Рассмотрим вариант Г_6,7=5100 Удалим из матрицы стоимости строку 6 и столбец 7, и присвоим элементу (7,6) значение бесконечности. Внесем в текущий ориентированный граф дугу (6,7)

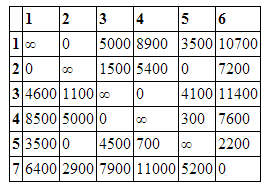
В строке 7 и столбце 6 отсутствует элемент равный ∞. Присвоим элементу (7,6) значение бесконечности чтобы избежать преждевременногог замыкания контура. Текущая Нижняя граница=27700 Нижняя граница равна сумме всех вычтенных элементов в строках и столбцах. Итоговое значение нижней границы должно совпасть с длиной результирующего контура. Найдем минимальные элементы в каждой строке и затем вычтем его из остальных элементов строки (минимальные элементы записаны напротив соответствующих строк). Получим матрицу представленную ниже.

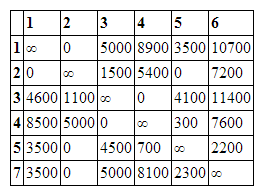
То же проделаем и со столбцами, не содержащими нуля. Получим матрицу, содержащую нули в каждой строке и каждом столбце.

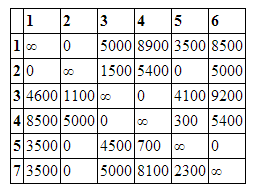
Для каждого нулевого элемента рассчитаем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Сij=0) и наименьшего элемента j столбца. Г_1,2=3500, Г_2,1=3500, Г_2,5=300, Г_3,4=1800, Г_4,3=1800, Г_5,2=0, Г_5,6=5000, Г_7,2=2300,  Максимальное значение имеет Г_5,6=5000 Удалим из матрицы стоимости строку 5 и столбец 6. Внесем в текущий ориентированный граф дугу (5,6)

	1	2	3	4	5
1	∞	0	5000	8900	3500
2	0	∞	1500	5400	0
3	4600	1100	∞	0	4100
4	8500	5000	0	∞	300
7	3500	0	5000	8100	2300

В строке 7 и столбце 5 отсутствует элемент равный ∞. Присвоим элементу (7,5) значение бесконечности чтобы избежать преждевременногог замыкания контура. Текущая Нижняя граница=32800 Найдем минимальные элементы в каждой строке и затем вычтем его из остальных элементов строки (минимальные элементы записаны напротив соответствующих строк). Получим матрицу представленную ниже.

	1	2	3	4	5
1	∞	0	5000	8900	3500
2	0	∞	1500	5400	0
3	4600	1100	∞	0	4100
4	8500	5000	0	∞	300
7	3500	0	5000	8100	∞

То же проделаем и со столбцами, не содержащими нуля. Получим матрицу, содержащую нули в каждой строке и каждом столбце.

	1	2	3	4	5
1	∞	0	5000	8900	3500
2	0	∞	1500	5400	0
3	4600	1100	∞	0	4100
4	8500	5000	0	∞	300
7	3500	0	5000	8100	∞

Для каждого нулевого элемента рассчитаем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Сij=0) и наименьшего элемента j столбца. Г_1,2=3500, Г_2,1=3500, Г_2,5=300, Г_3,4=6500, Г_4,3=1800, Г_7,2=3500,  Максимальное значение имеет Г_3,4=6500 Удалим из матрицы стоимости строку 3 и столбец 4. Внесем в текущий ориентированный граф дугу (3,4)

	1	2	3	5
1	∞	0	5000	3500
2	0	∞	1500	0
4	8500	5000	0	300
7	3500	0	5000	∞

В строке 4 и столбце 3 отсутствует элемент равный ∞. Присвоим элементу (4,3) значение бесконечности чтобы избежать преждевременногог замыкания контура. Текущая Нижняя граница=32800 Найдем минимальные элементы в каждой строке и затем вычтем его из остальных элементов строки (минимальные элементы записаны напротив соответствующих строк). Получим матрицу представленную ниже.

	1	2	3	5
1	∞	0	5000	3500
2	0	∞	1500	0
4	8200	4700	∞	0
7	3500	0	5000	∞

То же проделаем и со столбцами, не содержащими нуля. Получим матрицу, содержащую нули в каждой строке и каждом столбце.

	1	2	3	5
1	∞	0	3500	3500
2	0	∞	0	0
4	8200	4700	∞	0
7	3500	0	3500	∞

Для каждого нулевого элемента рассчитаем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Сij=0) и наименьшего элемента j столбца. Г_1,2=3500, Г_2,1=3500, Г_2,3=3500, Г_2,5=0, Г_4,5=4700, Г_7,2=3500,  Максимальное значение имеет Г_4,5=4700 Удалим из матрицы стоимости строку 4 и столбец 5. Внесем в текущий ориентированный граф дугу (4,5)

	1	2	3
1	∞	0	3500
2	0	∞	0
7	3500	0	3500

В строке 7 и столбце 3 отсутствует элемент равный ∞. Присвоим элементу (7,3) значение бесконечности чтобы избежать преждевременногог замыкания контура. Текущая Нижняя граница=34600 Найдем минимальные элементы в каждой строке и затем вычтем его из остальных элементов строки (минимальные элементы записаны напротив соответствующих строк). Получим матрицу представленную ниже.

	1	2	3
1	∞	0	3500
2	0	∞	0
7	3500	0	∞

То же проделаем и со столбцами, не содержащими нуля. Получим матрицу, содержащую нули в каждой строке и каждом столбце.

	1	2	3
1	∞	0	3500
2	0	∞	0
7	3500	0	∞

Для каждого нулевого элемента рассчитаем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Сij=0) и наименьшего элемента j столбца. Г_1,2=3500, Г_2,1=3500, Г_2,3=3500, Г_7,2=3500,  В результате сравнения мы получили 4 одинаковых максимальных Г=3500. Это означает что алгоритм разветвляется и мы должны рассмотреть все получившиеся варианты поочередно.Рассмотрим вариант Г_1,2=3500 Удалим из матрицы стоимости строку 1 и столбец 2, и присвоим элементу (2,1) значение бесконечности. Внесем в текущий ориентированный граф дугу (1,2)

	1	3
2	0	0
7	3500	∞

В строке 2 и столбце 1 отсутствует элемент равный ∞. Присвоим элементу (2,1) значение бесконечности чтобы избежать преждевременногог замыкания контура. Текущая Нижняя граница=34600 После того, как ранг матрицы становится равным двум мы получаем нули в каждой ее строке и столбце (добавив как и ранее вычтеные элементы матрицы к нижней границе), и добавляем к маршруту комивояжера дуги которым соответствуют нулевые элементы. НГр=38100 Маршрут коммивояжера включает в себя дуги:, (6, 7), (5, 6), (3, 4), (4, 5), (1, 2), (2, 3), (7, 1) ------------------------------------------------------------------------- Вернемся к возникшему у нас ветвлению и рассмотрим случай при котором максимальное значение имеет Г_7,2. Удалим из матрицы стоимости строку 2 и столбец 7. Внесем в текущий ориентированный граф дугу (7,2)

	1	3
1	∞	3500
2	0	0

В строке 2 и столбце 3 отсутствует элемент равный ∞. Присвоим элементу (2,3) значение бесконечности чтобы избежать преждевременногог замыкания контура. После того, как ранг матрицы становится равным двум мы получаем нули в каждой ее строке и столбце (добавив как и ранее вычтеные элементы матрицы к нижней границе), и добавляем к маршруту комивояжера дуги которым соответствуют нулевые элементы. НГр=38100 Маршрут коммивояжера включает в себя дуги:, (6, 7), (5, 6), (3, 4), (4, 5), (7, 2), (1, 3), (2, 1) ------------------------------------------------------------------------- Вернемся к возникшему у нас ветвлению и рассмотрим случай при котором максимальное значение имеет Г_2,3. Удалим из матрицы стоимости строку 3 и столбец 2. Внесем в текущий ориентированный граф дугу (2,3)

	1	2
1	∞	0
7	3500	0

В строке 7 и столбце 2 отсутствует элемент равный ∞. Присвоим элементу (7,2) значение бесконечности чтобы избежать преждевременногог замыкания контура. После того, как ранг матрицы становится равным двум мы получаем нули в каждой ее строке и столбце (добавив как и ранее вычтеные элементы матрицы к нижней границе), и добавляем к маршруту комивояжера дуги которым соответствуют нулевые элементы. НГр=38100 Маршрут коммивояжера включает в себя дуги:, (6, 7), (5, 6), (3, 4), (4, 5), (2, 3), (1, 2), (7, 1) ------------------------------------------------------------------------- Вернемся к возникшему у нас ветвлению и рассмотрим случай при котором максимальное значение имеет Г_2,1. Удалим из матрицы стоимости строку 1 и столбец 2. Внесем в текущий ориентированный граф дугу (2,1)

	2	3
1	0	3500
7	0	∞

В строке 1 и столбце 2 отсутствует элемент равный ∞. Присвоим элементу (1,2) значение бесконечности чтобы избежать преждевременногог замыкания контура. После того, как ранг матрицы становится равным двум мы получаем нули в каждой ее строке и столбце (добавив как и ранее вычтеные элементы матрицы к нижней границе), и добавляем к маршруту комивояжера дуги которым соответствуют нулевые элементы. НГр=38100 Маршрут коммивояжера включает в себя дуги:, (6, 7), (5, 6), (3, 4), (4, 5), (2, 1), (1, 3), (7, 2) ------------------------------------------------------------------------- Вернемся к возникшему у нас ветвлению и рассмотрим случай при котором максимальное значение имеет Г_7,6. Удалим из матрицы стоимости строку 6 и столбец 7. Внесем в текущий ориентированный граф дугу (7,6)

	1	2	3	4	5	7
1	∞	0	5000	8900	3500	6800
2	0	∞	1500	5400	0	3300
3	4600	1100	∞	0	4100	7900
4	8500	5000	0	∞	300	11000
5	3500	0	4500	700	∞	5600
6	10300	6800	11400	7600	1800	0

В строке 6 и столбце 7 отсутствует элемент равный ∞. Присвоим элементу (6,7) значение бесконечности чтобы избежать преждевременногог замыкания контура. Найдем минимальные элементы в каждой строке и затем вычтем его из остальных элементов строки (минимальные элементы записаны напротив соответствующих строк). Получим матрицу представленную ниже.

	1	2	3	4	5	7
1	∞	0	5000	8900	3500	6800
2	0	∞	1500	5400	0	3300
3	4600	1100	∞	0	4100	7900
4	8500	5000	0	∞	300	11000
5	3500	0	4500	700	∞	5600
6	8500	5000	9600	5800	0	∞

То же проделаем и со столбцами, не содержащими нуля. Получим матрицу, содержащую нули в каждой строке и каждом столбце.

	1	2	3	4	5	7
1	∞	0	5000	8900	3500	3500
2	0	∞	1500	5400	0	0
3	4600	1100	∞	0	4100	4600
4	8500	5000	0	∞	300	7700
5	3500	0	4500	700	∞	2300
6	8500	5000	9600	5800	0	∞

Для каждого нулевого элемента рассчитаем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Сij=0) и наименьшего элемента j столбца.
Г_1,2=3500, Г_2,1=3500, Г_2,5=0, Г_2,7=2300, Г_3,4=1800, Г_4,3=1800, Г_5,2=700, Г_6,5=5000, 
Максимальное значение имеет Г_6,5=5000
Удалим из матрицы стоимости строку 6 и столбец 5. Внесем в текущий ориентированный граф дугу (6,5)

	1	2	3	4	7
1	∞	0	5000	8900	3500
2	0	∞	1500	5400	0
3	4600	1100	∞	0	4600
4	8500	5000	0	∞	7700
5	3500	0	4500	700	2300

В строке 5 и столбце 7 отсутствует элемент равный ∞. Присвоим элементу (5,7) значение бесконечности чтобы избежать преждевременногог замыкания контура. Текущая Нижняя граница=32800 Найдем минимальные элементы в каждой строке и затем вычтем его из остальных элементов строки (минимальные элементы записаны напротив соответствующих строк). Получим матрицу представленную ниже.

	1	2	3	4	7
1	∞	0	5000	8900	3500
2	0	∞	1500	5400	0
3	4600	1100	∞	0	4600
4	8500	5000	0	∞	7700
5	3500	0	4500	700	∞

То же проделаем и со столбцами, не содержащими нуля. Получим матрицу, содержащую нули в каждой строке и каждом столбце.

	1	2	3	4	7
1	∞	0	5000	8900	3500
2	0	∞	1500	5400	0
3	4600	1100	∞	0	4600
4	8500	5000	0	∞	7700
5	3500	0	4500	700	∞

Для каждого нулевого элемента рассчитаем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Сij=0) и наименьшего элемента j столбца. Г_1,2=3500, Г_2,1=3500, Г_2,7=3500, Г_3,4=1800, Г_4,3=6500, Г_5,2=700,  Максимальное значение имеет Г_4,3=6500 Удалим из матрицы стоимости строку 4 и столбец 3. Внесем в текущий ориентированный граф дугу (4,3)

	1	2	4	7
1	∞	0	8900	3500
2	0	∞	5400	0
3	4600	1100	0	4600
5	3500	0	700	∞

В строке 3 и столбце 4 отсутствует элемент равный ∞. Присвоим элементу (3,4) значение бесконечности чтобы избежать преждевременногог замыкания контура. Текущая Нижняя граница=32800 Найдем минимальные элементы в каждой строке и затем вычтем его из остальных элементов строки (минимальные элементы записаны напротив соответствующих строк). Получим матрицу представленную ниже.

	1	2	4	7
1	∞	0	8900	3500
2	0	∞	5400	0
3	3500	0	∞	3500
5	3500	0	700	∞

То же проделаем и со столбцами, не содержащими нуля. Получим матрицу, содержащую нули в каждой строке и каждом столбце.

	1	2	4	7
1	∞	0	8200	3500
2	0	∞	4700	0
3	3500	0	∞	3500
5	3500	0	0	∞

Для каждого нулевого элемента рассчитаем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Сij=0) и наименьшего элемента j столбца. Г_1,2=3500, Г_2,1=3500, Г_2,7=3500, Г_3,2=3500, Г_5,2=0, Г_5,4=4700,  Максимальное значение имеет Г_5,4=4700 Удалим из матрицы стоимости строку 5 и столбец 4. Внесем в текущий ориентированный граф дугу (5,4)

	1	2	7
1	∞	0	3500
2	0	∞	0
3	3500	0	3500

В строке 3 и столбце 7 отсутствует элемент равный ∞. Присвоим элементу (3,7) значение бесконечности чтобы избежать преждевременногог замыкания контура. Текущая Нижняя граница=34600 Найдем минимальные элементы в каждой строке и затем вычтем его из остальных элементов строки (минимальные элементы записаны напротив соответствующих строк). Получим матрицу представленную ниже.

	1	2	7
1	∞	0	3500
2	0	∞	0
3	3500	0	∞

То же проделаем и со столбцами, не содержащими нуля. Получим матрицу, содержащую нули в каждой строке и каждом столбце.

	1	2	7
1	∞	0	3500
2	0	∞	0
3	3500	0	∞

Для каждого нулевого элемента рассчитаем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Сij=0) и наименьшего элемента j столбца. Г_1,2=3500, Г_2,1=3500, Г_2,7=3500, Г_3,2=3500,  В результате сравнения мы получили 4 одинаковых максимальных Г=3500. Это означает что алгоритм разветвляется и мы должны рассмотреть все получившиеся варианты поочередно.Рассмотрим вариант Г_1,2=3500 Удалим из матрицы стоимости строку 1 и столбец 2, и присвоим элементу (2,1) значение бесконечности. Внесем в текущий ориентированный граф дугу (1,2)

	1	7
2	0	0
3	3500	∞

В строке 2 и столбце 1 отсутствует элемент равный ∞. Присвоим элементу (2,1) значение бесконечности чтобы избежать преждевременногог замыкания контура. Текущая Нижняя граница=34600 После того, как ранг матрицы становится равным двум мы получаем нули в каждой ее строке и столбце (добавив как и ранее вычтеные элементы матрицы к нижней границе), и добавляем к маршруту комивояжера дуги которым соответствуют нулевые элементы. НГр=38100 Маршрут коммивояжера включает в себя дуги:, (7, 6), (6, 5), (4, 3), (5, 4), (1, 2), (2, 7), (3, 1) ------------------------------------------------------------------------- Вернемся к возникшему у нас ветвлению и рассмотрим случай при котором максимальное значение имеет Г_3,2. Удалим из матрицы стоимости строку 2 и столбец 3. Внесем в текущий ориентированный граф дугу (3,2)

	1	7
1	∞	3500
2	0	0

В строке 2 и столбце 7 отсутствует элемент равный ∞. Присвоим элементу (2,7) значение бесконечности чтобы избежать преждевременногог замыкания контура. После того, как ранг матрицы становится равным двум мы получаем нули в каждой ее строке и столбце (добавив как и ранее вычтеные элементы матрицы к нижней границе), и добавляем к маршруту комивояжера дуги которым соответствуют нулевые элементы. НГр=38100 Маршрут коммивояжера включает в себя дуги:, (7, 6), (6, 5), (4, 3), (5, 4), (3, 2), (1, 7), (2, 1) ------------------------------------------------------------------------- Вернемся к возникшему у нас ветвлению и рассмотрим случай при котором максимальное значение имеет Г_2,7. Удалим из матрицы стоимости строку 7 и столбец 2. Внесем в текущий ориентированный граф дугу (2,7)

	1	2
1	∞	0
3	3500	0

В строке 3 и столбце 2 отсутствует элемент равный ∞. Присвоим элементу (3,2) значение бесконечности чтобы избежать преждевременногог замыкания контура. После того, как ранг матрицы становится равным двум мы получаем нули в каждой ее строке и столбце (добавив как и ранее вычтеные элементы матрицы к нижней границе), и добавляем к маршруту комивояжера дуги которым соответствуют нулевые элементы. НГр=38100 Маршрут коммивояжера включает в себя дуги:, (7, 6), (6, 5), (4, 3), (5, 4), (2, 7), (1, 2), (3, 1) ------------------------------------------------------------------------- Вернемся к возникшему у нас ветвлению и рассмотрим случай при котором максимальное значение имеет Г_2,1. Удалим из матрицы стоимости строку 1 и столбец 2. Внесем в текущий ориентированный граф дугу (2,1)

	2	7
1	0	3500
3	0	∞

В строке 1 и столбце 2 отсутствует элемент равный ∞. Присвоим элементу (1,2) значение бесконечности чтобы избежать преждевременногог замыкания контура. После того, как ранг матрицы становится равным двум мы получаем нули в каждой ее строке и столбце (добавив как и ранее вычтеные элементы матрицы к нижней границе), и добавляем к маршруту комивояжера дуги которым соответствуют нулевые элементы. НГр=38100 Маршрут коммивояжера включает в себя дуги:, (7, 6), (6, 5), (4, 3), (5, 4), (2, 1), (1, 7), (3, 2) ------------------------------------------------------------------------- Мы рассмотрели все возможные ветви алгоритма, теперь необходимо выбрать из полученых в результате рассмотрения каждой ветви значений нижней границы - минимальное. Это и будет оптимальной длиной пути коммивояжера Минимальное значение имеет НГр=38100 Соответствующий оптимальный контур включет дуги:, (6, 7), (5, 6), (3, 4), (4, 5), (1, 2), (2, 3), (7, 1)